/MAT/LAW18 (THERM)

ブロックフォーマットのキーワードこの材料則は熱材料を記述します。

フォーマット

(1)	(2)	(3)	(4)	(5)	(7)
/MAT/LAW18/`mat_ID`または/MAT/THERM/`mat_ID`
`mat_title`
$ρ_{i}$		$ρ_{0}$
$ρ_{0} C_{p}$		`A`		`B`
`fct_ID`_T	`T`₀		`Fscale`_T
`fct_ID`_sph	`fct_ID`_as	`Fscale`_sph		`Fscale`_E	`Fscale`_K

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
$ρ_{0}$	E.O.S（状態方程式）で使用される基準密度デフォルト = $ρ_{0}$ = $ρ_{i}$ （実数）	$[\frac{kg}{m^{3}}]$
$ρ_{0} C_{p}$	比熱（実数）	$[\frac{kg}{s^{3} \cdot m \cdot K}]$
`A`	伝導係数A （実数）	$[\frac{W}{m^{2} K}]$
`B`	伝導係数B （実数）
`fct_ID`_T	Tの関数`f(t)`の識別子。 9 = 0 `T`は計算されます = n `T`=`T`₀⋅`f`(`t`) （整数）
`T`₀	初期温度デフォルト = 300K（実数）	$[K]$
`Fscale`_T	時間スケールファクター（実数）
`fct_ID`_sph	温度とエネルギーの関数g(T, E)の識別子 7 （整数）
`fct_ID`_as	伝導と温度の関数h(k, T)の識別子（整数）
`Fscale`_sph	温度スケールファクター（実数）	$[K]$
`Fscale`_E	エネルギースケールファクター（実数）	$[J]$
`Fscale`_K	伝導スケールファクター（実数）	$[\frac{W}{m^{2} K}]$

この材料は以下のいずれかとして使用できます。
- 純熱学的材料として（行4だけが読み出されます）
- 境界条件（温度または流束）として（行5を使用します）
$k$ （熱伝導）は、下記のように計算されます：(1)
$k = A + B \cdot T$
α（熱拡散）は下記のように計算されます：(2)
$α = k / ρ_{0} C_{p}$

ここで、 $C_{p}$ は、定圧における熱容量です。
$k$ （熱伝導）は曲線 $f c t _ I D_{a s} = k (T)$ によって定義されます。
α（熱拡散）は曲線fct_ID_sph $α = k / ρ_{0} C_{p}$ を使用して $\frac{d E}{d T} = C_{p}$ で求められます。
関数g(T, E)は以下のような曲線になります：

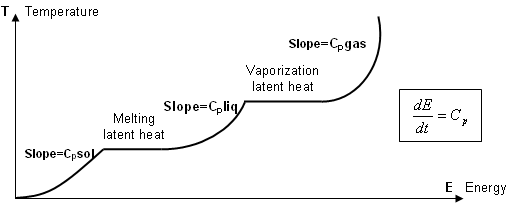
図 1.
fct_ID_sph ≠ 0の場合、(3)
$E_{s p e c i f i c} = \frac{\frac{E_{int}}{ρ_{0}}}{F s c a l e_{E}}$

$T = f_{s p h} (E_{s p e c i f i c}) \cdot F s c a l e_{s p h}$

ここで、 $f_{s p h}$ はfct_ID_sphの関数です。
fct_ID_sph = 0の場合、(4)
$T = \frac{E_{int}}{sph}$

ここで、 $S p h = ρ_{0} C_{p} = S p e c i f i c H e a t$
fct_ID_T ≠ 0の場合、(5)
$T = f (T i m e) \cdot T_{0}$

ここで、 $T i m e = T i m e \cdot F s c a l e_{T}$ ； $E_{int} = T \cdot s p h$ 。
fct_ID_as ≠ 0の場合、
(6)
$T = \frac{T}{F s c a l e_{s p h}}$

$A = f_{a s} (T) \cdot F s c a l e_{E}$ 、 $B = 0$

ここで、 $f_{a s}$ はfct_ID_asの関数です。