ギアタイプジョイントは他の運動学的ジョイントよりもより複雑です。これにはLagrange乗数法を用い、全ての他のLagrange乗数法の運動条件と適合しますが、古典的な運動条件とは一切適合しません。
以下にこれらの3つのジョイントの例を説明します:
- 回転ギアタイプジョイント
- ラックアンドピニオンジョイント
- ディファレンシャルギアジョイント
慣性と質量は全ての節点に付加されます。MPCジョイントにより、節点の速度間の関係が設定されます。MPCは質量のない節点の並進自由度と慣性のない節点の回転自由度に与えることはできません。
回転ギアタイプジョイント
このジョイントは入力と出力節点の間の回転速度の関係を与えるのに用いられます:
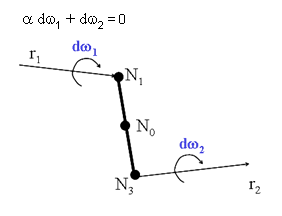
図 1. 回転タイプジョイント
ギアジョイント節点の並進速度は、剛性リンクの関係による制約を受けます。回転自由度に関しては、節点
N1と
N2の速度の間に、局所座標系で測定された、スケールファクターが与えられます。対応する拘束方程式は:
ここで、
は、節点N1およびN2の剛体回転速度に対する相対回転速度です。
ラックアンドピニオンジョイント
このジョイントは節点の回転速度を次のように並進速度に転換します:
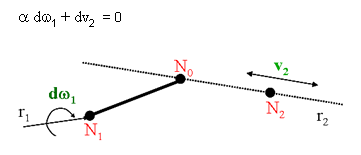
図 2. ラックアンドピニオンジョイント
これらの速度の拘束方程式は:
(1)
(2)
(3)
ディファレンシャルギアジョイント
このジョイントは、1つの入力節点と2つの出力節点の間の回転速度の関係を次のように与えます:

図 3. ディファレンシャルョイントタイプ
ディファレンシャルギアジョイントの回転速度は、下記の関係による制約を受けます:
(4)
(5)
(6)


