Patran

Patranの基準に従った2Dおよび3D要素の品質計算が行われます。

ここにリストされていない要素チェックは、このソルバーのチェックの標準セットには含まれていないため、HyperMeshのチェック手法を使用します。

2Dおよび3D要素チェック

これらのチェックは、両方のタイプの要素に適用されますが、3D要素に用いられる際は通常、要素の各フェイスに適用されます。最悪の値をもつフェイスが、3D要素の全体の品質値としてレポートされます。
Aspect Ratio (triangle)
三角形の辺の長さをその辺から向かい側の節点までの高さで割り、3の平方根の2分の1を掛けます。完全な正三角形では、この式の値は1となります。この計算を、三角形の３つの辺についてそれぞれ実行し、得られた値のうち最も大きいものが縦横比としてレポートされます。


A s p e c t = 3 h 2 2 h 1
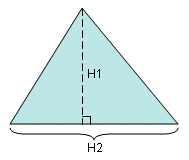
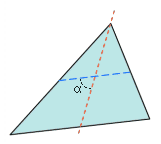
図 1. Aspect Ratio for Triangles
Aspect Ratio (quads)
要素が平坦ではない場合、要素のコーナー法線の平均に基づいたプレーンに投影されます。後続の計算はすべて、元の（湾曲した）要素ではなく、この投影された要素をベースとします。
次に要素の向かい合うエッジの中点同士を結ぶ1つのラインが描かれます。これらのラインは互いに、もしくは要素エッジのいずれかに必ずしも垂直ではありませんが、4つの中点を与えます。
次に、これら1つのラインのそれぞれについて、向かい合う1つのエッジがそれぞれの中点でラインと垂直に交わり、残りの1つのエッジはもう一方のラインの終端をそれぞれ通過するような長方形が作成されます。この結果、それぞれのラインに垂直な1つの長方形ができあがります。


図 2. Aspect Ratio for Quads
最後に、1つの長方形を比較し、最長の辺と最短の辺の比が大きいほうを求めます。この値が、四角形要素の縦横比としてレポートされます。完全な正四角形（正方形）の縦横比は1で、この比が大きいほど、正方形からの偏差が大きくなります。
Interior Angles
内部角度の最大および最小値は、三角形要素と四角形要素についてそれぞれ別々に評価されます。
Jacobian
要素の理想的または“完全”な形状（例えば三角形であれば正三角形）からの逸脱の度合いを示します。ヤコビアン値は0.0から1.0の範囲の値で、1.0は完全な形状の要素を表わします。ヤコビアン比の決定子は、全体座標スペースにフィットさせるために必要なパラメトリックスペースの局所ストレッチングに関係しています。
HyperWorksは､要素の各積分点（ガウス点とも呼ばれる）もしくは要素のコーナー節点におけるヤコビアンマトリックスの決定要素を求め､最小値と最大値間の比率をレポートします。ガウス点におけるヤコビアン評価の場合、値が0.7以上であれば、通常許容されます。どちらの評価方法（ガウス点またはコーナー節点）を用いるかは、Check Element Settingsウィンドウで選ぶことができます。
Length (min)
要素の最小長は、以下の1つの方法のうちのいずれかで計算されます：
  • 要素の最も短いエッジ。この方法は、四面体以外の3D要素に使用されます。
  • コーナー節点から向かい合うエッジ（四面体要素の場合はフェイス）への最短距離（正規化された最小の高さ）。


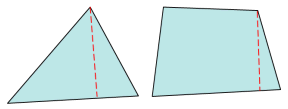
図 3. Length (min)
Skew (triangle)
Patranは三角形のスキューを、三角形の節点のうちの１つから向かい合う辺の中点へライン、および残りの２つの辺の中点を結ぶラインを描きます。


図 4. Skew for Triangles
作成されたこれらのラインが成す角度を90度と比較し、正方形からの偏差を求めます。この計算を、三角形の残る２つの辺について繰り返し、得られた３つの角度のうち最も大きいものが要素のスキューとしてレポートされます。
Skew (Quad)
スキューのチェックはまず、４つの要素エッジを二等分することから始まります。これにより、４つのコーナーのベクトル平均位置に原点が作成されます。ここで、x-軸は原点からエッジ2の二等分線に延びています。次に、原点からエッジ3の中点へ延びるベクトルとx-軸の乗積を求め、z-軸を定義します。x-、およびz-軸が定義されると、その乗積からy-軸が定義されます。


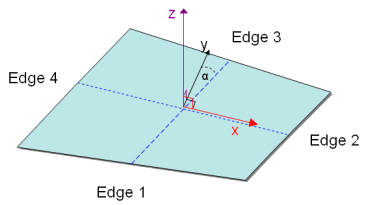
図 5. Skew for Quads
最後に、エッジ1とエッジ3を二等分するラインとy-軸の間の角度αを90度から引き、要素のスキュー角とします。
Taper
Patranはテーパをまず、コーナー節点を平均して要素の中心を求め、このセンターとコーナー節点の間にラインを引いて要素を４つの三角形に分割します。
t a p e r = 4 α s m a l l e s t α 1 + α 2 + α 3 + α 4
テーパの計算は単に、最も小さい三角形の面積をすべての三角形の面積の平均で割るか、もしくは最も小さい三角形の面積を４倍し、それを４つすべての三角形の面積の和で割ることによって行います。
t a p e r = 4 α s m a l l e s t α 1 + α 2 + α 3 + α 4
注: 表示の一貫性を保持するために、HyperWorksは同値のテーパをレポートします。テーパは上記のように決定されますが、1から引くと、ゼロから1までの数値が得られます。したがって、要素のテーパが小さくなるにつれて、レポートされる値はゼロ（完全な正方形）に近づきます。三角形要素には、"failed"（不合格）である四角形要素とされることを回避するため、値0が割り当てられます。
Warpage
ねじれのチェックでは、要素のエッジを二等分し、要素コーナーのベクトル平均位置のポイントを作成します。このポイントは、プレーンのベース節点となり、プレーンのx-軸はベース節点から要素のエッジ2の二等分線に延びています。プレーンの法線（z-軸）は、原点からエッジ3の二等分線へ延びるベクトルとx-軸の乗積の方向です。したがって、四角形要素の各コーナーは、プレーンから同じ距離hとなります。次にPatranは、各半エッジの長さを求め、最も短い半エッジ長（L）に対するhの比のアークサインを計算します。
Θ = sin − 1 h L

3D要素のみのチェック

Vol. Aspect Ratio （四面体要素）
Patranは四面体要素の縦横比を、頂角の高さと向かい合うフェイスの面積の２分の１との比を計算することによって求めます。この計算を各頂点について繰り返し、最も大きい比を求めます。


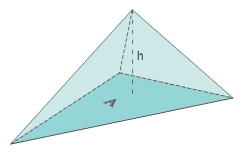
図 6. Vol. Aspect Ratio（四面体要素）
次にPatranは、求められた最も大きい値を0.805927(正四面体に対応する比)で掛けます。その結果値が、要素の縦横比としてレポートされます。値1が、完全な正四面体を示します。
Vol. Aspect Ratio （ピラミッド）
要素エッジの最長と最短の比。
Vol. Aspect Ratio （ウェッジ要素）
このチェックではまず、要素の三角形フェイスを平均し、三角形の中立面を作成します。次に、中立面の縦横比を求めます（三角形要素の場合）。続いて、ウェッジ要素の平均の高さ（h1）を中立面の最も長いエッジ長（h2）と比較します。


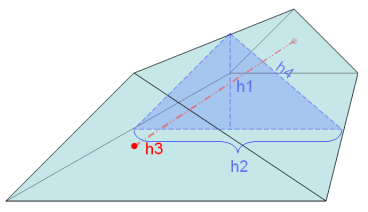
図 7. Vol. Aspect Ratio（ウェッジ要素）
ウェッジの高さh1がエッジ長h2を上回る場合、そのウェッジの縦横比は、中立面の縦横比にh2を掛け、その値を三角形のフェイス間の平均距離（h3）で割ったものと等しくなります。
ウェッジの高さh1がエッジ長h2より小さい場合、そのウェッジの縦横比は、中立面の縦横比、もしくは、最大エッジ長h2を三角形のフェイス間の平均距離（h3）で割ったもののいずれかとなります。
A s p e c t   R a t i o = h 4 h 3 3 h 2 2 h 1
Vol. Aspect Ratio （六面体要素）
六面体要素の各フェイスはねじれた四角形として扱われ、そのセンタ－ポイントが求められます。体積縦横比は単に、向かい合う２つのフェイスのセンターポイント間の最大距離hと最小距離との比です。


A s p e c t   R a t i o = max ( h 1 , h 2 , h 3 ) min ( h 1 , h 2 , h 3 )
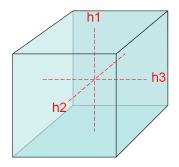
図 8. Vol. Aspect Ratio（六面体要素）