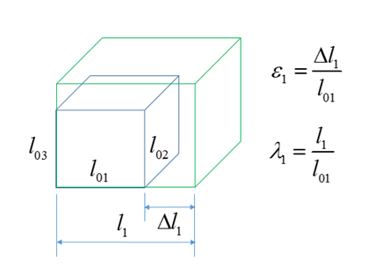
この材料モデルは、Ogden、Neo-Hookean、またはMooney-Rivlin材料モデルを使用して指定された超弾性、粘性、および非圧縮性の材料を定義します。この法則は、通常、非圧縮性のゴム、ポリマー、フォーム、およびエラストマーのモデル化に使用されます。この材料は、シェル要素とソリッド要素に使用できます。
LAW42は、以下のOgden材料モデルのひずみエネルギー密度表現を使用します。
(3)
W
(
λ
1
,
λ
2
,
λ
3
)
=
∑
p
=
1
5
μ
p
α
p
(
λ
¯
1
α
p
+
λ
¯
2
α
p
+
λ
¯
3
α
p
−
3
)
+
K
2
(
J
−
1
)
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGxbWaae
WaaeaacqaH7oaBdaWgaaWcbaGaaGymaaqabaGccaGGSaGaeq4UdW2a
aSbaaSqaaiaaikdaaeqaaOGaaiilaiabeU7aSnaaBaaaleaacaaIZa
aabeaaaOGaayjkaiaawMcaaiabg2da9maaqahabaWaaSaaaeaacqaH
8oqBdaWgaaWcbaGaamiCaaqabaaakeaacqaHXoqydaWgaaWcbaGaam
iCaaqabaaaaOWaaeWaaeaadaqdaaqaaiabeU7aSbaadaWgaaWcbaGa
aGymaaqabaGcdaahaaWcbeqaaiabeg7aHnaaBaaameaacaWGWbaabe
aaaaGccqGHRaWkdaqdaaqaaiabeU7aSbaadaWgaaWcbaGaaGOmaaqa
baGcdaahaaWcbeqaaiabeg7aHnaaBaaameaacaWGWbaabeaaaaGccq
GHRaWkdaqdaaqaaiabeU7aSbaadaWgaaWcbaGaaG4maaqabaGcdaah
aaWcbeqaaiabeg7aHnaaBaaameaacaWGWbaabeaaaaGccqGHsislca
aIZaaacaGLOaGaayzkaaaaleaacaWGWbGaeyypa0JaaGymaaqaaiaa
iwdaa0GaeyyeIuoakiabgUcaRmaalaaabaGaam4saaqaaiaaikdaaa
WaaeWaaeaacaWGkbGaeyOeI0IaaGymaaGaayjkaiaawMcaamaaCaaa
leqabaGaaGOmaaaaaaa@6C02@
ここで、
W
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGxbaaaa@373A@
ひずみエネルギー密度
λ
i
i th 主工学ストレッチ
J
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGkbaaaa@372D@
相対体積は次のように定義されます:
J
=
λ
1
⋅
λ
2
⋅
λ
3
=
ρ
0
ρ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGkbGaey
ypa0Jaeq4UdW2aaSbaaSqaaiaaigdaaeqaaOGaeyyXICTaeq4UdW2a
aSbaaSqaaiaaikdaaeqaaOGaeyyXICTaeq4UdW2aaSbaaSqaaiaaio
daaeqaaOGaeyypa0ZaaSaaaeaacqaHbpGCdaWgaaWcbaGaaGimaaqa
baaakeaacqaHbpGCaaaaaa@4A3F@
λ
¯
i
=
J
−
1
3
λ
i
偏差ストレッチ
α
p
μ
p
材料定数係数ペア。
5つまでの材料定数ペアを定義できます。
初期せん断弾性率
μ
および体積弾性率(
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGlbaaaa@372E@
)は、次のように与えられます:
(4)
μ
=
∑
p
=
1
5
μ
p
⋅
α
p
2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd0Maey
ypa0ZaaSaaaeaadaaeWbqaaiabeY7aTnaaBaaaleaacaWGWbaabeaa
kiabgwSixlabeg7aHnaaBaaaleaacaWGWbaabeaaaeaacaWGWbGaey
ypa0JaaGymaaqaaiaaiwdaa0GaeyyeIuoaaOqaaiaaikdaaaaaaa@4720@
および(5)
K
=
μ
⋅
2
(
1
+
ν
)
3
(
1
−
2
ν
)
ここで、
ν
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyVd4gaaa@37AF@
材料パラメータ
パラメータ
α
p
および
μ
p
は、初期せん断弾性率が以下となるように選択されなくてはなりません:
(6)
μ =
∑
p = 1
5
μ
p
⋅
α
p
2
> 0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd0Maey
ypa0ZaaSaaaeaadaaeWbqaaiabeY7aTnaaBaaaleaacaWGWbaabeaa
kiabgwSixlabeg7aHnaaBaaaleaacaWGWbaabeaaaeaacaWGWbGaey
ypa0JaaGymaaqaaiaaiwdaa0GaeyyeIuoaaOqaaiaaikdaaaGaeyOp
a4JaaGimaaaa@48E2@
材料の安定性のためには、各材料定数ペアが以下のとおりである必要があります:
(7)
μ
p
⋅
α
p
>
0
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH8oqBda
WgaaWcbaGaamiCaaqabaGccqGHflY1cqaHXoqydaWgaaWcbaGaamiC
aaqabaGccqGH+aGpcaaIWaaaaa@4015@
通常、Ogdenモデルは700%までのひずみに使用することができます。材料ペア
α
p
μ
p
Radioss で、もしくは別のフィッティングソフトウェアを介して行うことが可能です。
Neo-Hookeanモデル
Ogden材料モデルのシンプルなケースが、ひずみエネルギー密度関数の次の式を使用して表現可能なNeo-Hookenモデルです:
(8)
W =
C
10
(
I
1
− 3
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4vaiabg2
da9iaadoeadaWgaaWcbaGaaGymaiaaicdaaeqaaOWaaeWaaeaacaWG
jbWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaaG4maaGaayjkaiaawM
caaaaa@3F3E@
ここで、
I
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaaBa
aaleaacaaIXaaabeaaaaa@37AC@
右Cauchy-Greenテンソルの第1不変量
C
10
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaaIXaGaaGimaaqabaaaaa@3860@
材料の定数
この表現は、次の場合に、LAW42 Ogdenひずみエネルギー密度関数から求められます:
μ
1
= 2 ⋅
C
10
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd02aaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaaGOmaiabgwSixlaadoeadaWg
aaWcbaGaaGymaiaaicdaaeqaaaaa@3F13@
α
1
= 2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaaGOmaaaa@3A49@
μ
2
=
α
2
= 0
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd02aaS
baaSqaaiaaikdaaeqaaOGaeyypa0JaeqySde2aaSbaaSqaaiaaikda
aeqaaOGaeyypa0JaaGimaaaa@3DF6@
Neo-Hookeanモデルは、20%未満のひずみについてのみ正確であるシンプルなモデルです。
Mooney-Rivlinモデル
LAW42 Ogden材料モデルの少し複雑なケースが、ひずみエネルギー密度関数の次の式を使用して表現可能なMooney-Rivlinモデルです:
(9)
W =
C
10
(
I
1
− 3
) +
C
01
(
I
2
− 3
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4vaiabg2
da9iaadoeadaWgaaWcbaGaaGymaiaaicdaaeqaaOWaaeWaaeaacaWG
jbWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaaG4maaGaayjkaiaawM
caaiabgUcaRiaadoeadaWgaaWcbaGaaGimaiaaigdaaeqaaOWaaeWa
aeaacaWGjbWaaSbaaSqaaiaaikdaaeqaaOGaeyOeI0IaaG4maaGaay
jkaiaawMcaaaaa@4786@
ここで、
I
1
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaaBa
aaleaacaaIXaaabeaaaaa@37AC@
I
2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaaBa
aaleaacaaIXaaabeaaaaa@37AC@
右Cauchy-Greenテンソルの第1および第2不変量
C
10
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaaIXaGaaGimaaqabaaaaa@3860@
C
01
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4qamaaBa
aaleaacaaIXaGaaGimaaqabaaaaa@3860@
材料の定数
この表現は、次の場合に、LAW42 Ogdenひずみエネルギー密度関数から求められます:
μ
1
=
2
⋅
C
10
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd02aaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaaGOmaiabgwSixlaadoeadaWg
aaWcbaGaaGymaiaaicdaaeqaaaaa@3F13@
μ
2
=
−
2
⋅
C
01
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiVd02aaS
baaSqaaiaaikdaaeqaaOGaeyypa0JaeyOeI0IaaGOmaiabgwSixlaa
doeadaWgaaWcbaGaaGimaiaaigdaaeqaaaaa@4001@
α
1
=
2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaaGOmaaaa@3A49@
α
2
=
-2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySde2aaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaaGOmaaaa@3A49@
Mooney-Rivlin定数は、材料サプライヤーまたは試験会社から入手できます。入手できない場合、単軸試験データの曲線フィッティングがLAW69を用いてRadioss で、もしくは別のフィッティングソフトウェアを介して行うことが可能です。Mooney-Rivlin材料則は、100%までのひずみについて正確です。
ポアソン比と材料の非圧縮性
材料が真に非圧縮性である場合、
ν
=
0.5
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyVd4Maey
ypa0JaaGimaiaac6cacaaI1aaaaa@3AE0@
。しかしながら、これは無限体積弾性率、無限音速、ひいては無限に小さいソリッド要素
時間ステップ をもたらすため、実践的には使用するのは不可能です。
(10)
K
=
μ
⋅
2
(
1
+
ν
)
3
(
1
−
2
ν
)
=
μ
⋅
2
(
1
+
ν
)
3
(
1
−
2
*
0.5
)
=
∞
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4saiabg2
da9iabeY7aTjabgwSixpaalaaabaGaaGOmamaabmaabaGaaGymaiab
gUcaRiabe27aUbGaayjkaiaawMcaaaqaaiaaiodadaqadaqaaiaaig
dacqGHsislcaaIYaGaeqyVd4gacaGLOaGaayzkaaaaaiabg2da9iab
eY7aTjabgwSixpaalaaabaGaaGOmamaabmaabaGaaGymaiabgUcaRi
abe27aUbGaayjkaiaawMcaaaqaaiaaiodadaqadaqaaiaaigdacqGH
sislcaaIYaGaaiOkaiaaicdacaGGUaGaaGynaaGaayjkaiaawMcaaa
aacqGH9aqpcqGHEisPaaa@5C83@
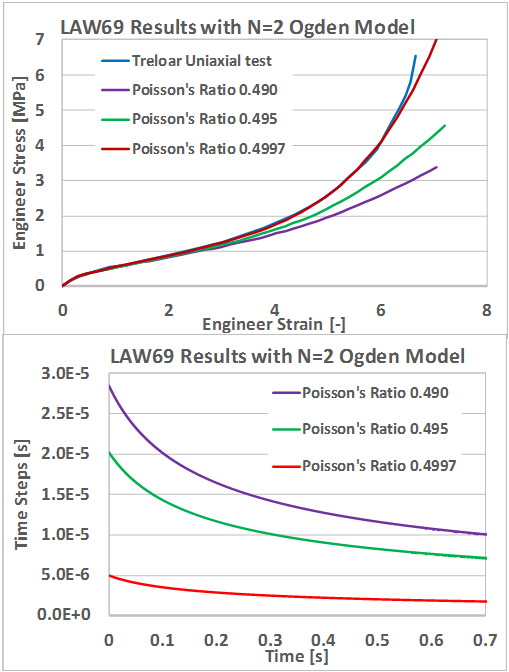
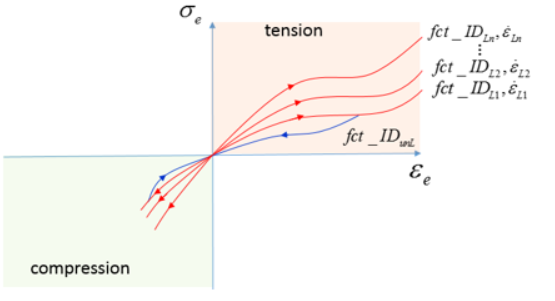
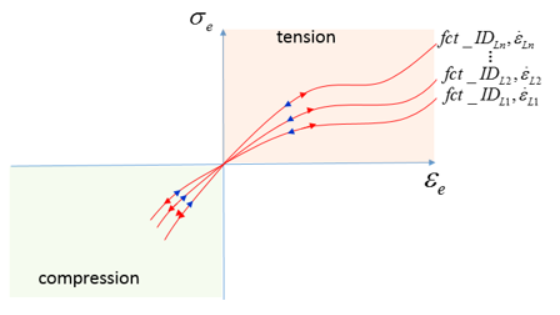
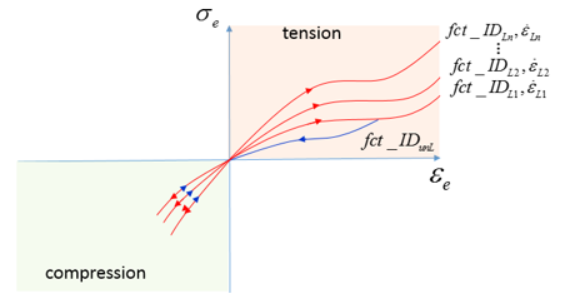
異なるポアソン比入力の影響は、図 2 に見られます。結果のうち最も大きな差は、より多くの量のひずみです。
ν
=
0.4997
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Jh9qqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH9oGBcq
GH9aqpcaaIWaGaaiOlaiaaisdacaaI5aGaaGyoaiaaiEdaaaa@3E7A@
ν
=
0.495
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Jh9qqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH9oGBcq
GH9aqpcaaIWaGaaiOlaiaaisdacaaI5aGaaGyoaiaaiEdaaaa@3E7A@
ν
=
0.495
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Jh9qqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH9oGBcq
GH9aqpcaaIWaGaaiOlaiaaisdacaaI5aGaaGyoaiaaiEdaaaa@3E7A@
ポアソン比と体積弾性率の影響は、他のOgden材料則と同様になります。
図 2.
陽解法シミュレーションの場合は、ポアソン比を高くすると、時間ステップ値の極端な減少や発散につながる可能性があります。
LAW42では、材料の非圧縮性は、密度の変化に比例して圧力を計算するペナルティアプローチを使用して求められます:
(11)
P
=
K
⋅
F
s
c
a
l
e
b
l
k
⋅
f
b
l
k
(
J
)
⋅
(
J
−
1
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGqbGaey
ypa0Jaam4saiabgwSixlaadAeacaWGZbGaam4yaiaadggacaWGSbGa
amyzamaaBaaaleaacaWGIbGaamiBaiaadUgaaeqaaOGaeyyXICTaci
OzamaaBaaaleaacaWGIbGaamiBaiaadUgaaeqaaOWaaeWaaeaacaWG
kbaacaGLOaGaayzkaaGaeyyXIC9aaeWaaeaacaWGkbGaeyOeI0IaaG
ymaaGaayjkaiaawMcaaaaa@5293@
ここで、
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGlbaaaa@372E@
体積弾性率
J
=
V
V
0
=
m
ρ
0
m
ρ
=
ρ
0
ρ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOsaiabg2
da9maalaaabaGaamOvaaqaaiaadAfadaWgaaWcbaGaaGimaaqabaaa
aOGaeyypa0ZaaSaaaeaacaWGTbGaeqyWdi3aaSbaaSqaaiaaicdaae
qaaaGcbaGaamyBaiabeg8aYbaacqGH9aqpdaWcaaqaaiabeg8aYnaa
BaaaleaacaaIWaaabeaaaOqaaiabeg8aYbaaaaa@4771@
質量が一定の場合に相対密度に簡易化される相対体積
f
b
l
k
(
J
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGMbWaaS
baaSqaaiaadkgacaWGSbGaam4AaaqabaGcdaqadaqaaiaadQeaaiaa
wIcacaGLPaaaaaa@3CA0@
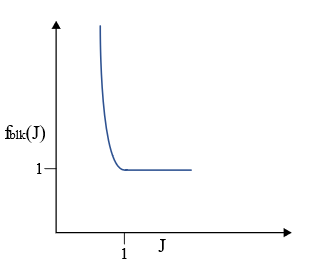
体積係数スケールファクターvs相対体積関数
F
s
c
a
l
e
b
l
k
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbGaam
4CaiaadogacaWGHbGaamiBaiaadwgadaWgaaWcbaGaamOyaiaadYga
caWGRbaabeaaaaa@3EBE@
右記の関数の横軸のスケールファクター;
f
b
l
k
(
J
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaaciGGMbWaaS
baaSqaaiaadkgacaWGSbGaam4AaaqabaGcdaqadaqaaiaadQeaaiaa
wIcacaGLPaaaaaa@3CA0@
超弾性材料の体積弾性率(
K
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGlbaaaa@372E@
)は一般的に非常に大きい値であり、非圧縮性条件(
J
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGkbaaaa@372D@
=1)を保持するために必要な圧力-抵抗を提供します。しかし、材料が圧縮し始めた場合(
J
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGkbaaaa@372D@
< 1)、体積係数値のスケーリングを
J
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGkbaaaa@372D@
の関数とすることが可能な
fct_ID blk 入力関数を含めることにより、体積弾性率を増加させることができます。デフォルトではスケーリングはなく、関数識別子が0であれば、体積スケーリング関数の値は1に等しくなります。密度のばらつきが小さくなるように、つまり、
J
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGkbaaaa@372D@
の値が1に近付き材料が非圧縮性であるよう、LAW42コンポーネントの材料密度を出力(
/ANIM/BRICK/DENS )し、確認することが推奨されます。
図 3. 体積弾性率スケールファクター関数fct_ID blk
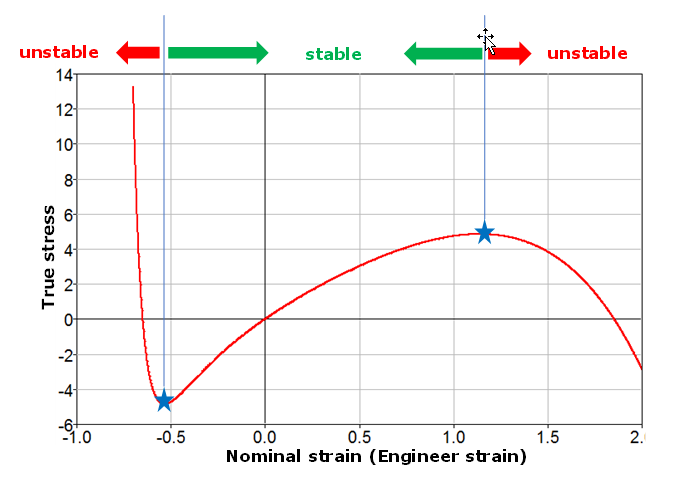
粘性(速度)効果
LAW42ではMaxwellモデル(剛性
G
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGhbWaaS
baaSqaaiaadMgaaeqaaaaa@3844@
とダンパ
η
i
を持つn個のスプリングの系として簡単に記述することができる)を使用した粘性(速度)効果がモデル化されます:
図 4. Maxwellモデル
Maxwellモデルは、Prony級数の入力(
G
i
,
τ
i
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4ramaaBa
aaleaacaWGPbaabeaakiaacYcacqaHepaDdaWgaaWcbaGaamyAaaqa
baaaaa@3B76@
)を使って表現されます。超弾性初期せん断弾性率
μ
は、Maxwellモデルの長期せん断弾性率
G
∞
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGhbWaaS
baaSqaaiabg6HiLcqabaaaaa@38C7@
と同じであり、
τ
i
は緩和時間です:
(12)
τ
i
=
η
i
G
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHepaDda
WgaaWcbaGaamyAaaqabaGccqGH9aqpdaWcaaqaaiabeE7aOnaaBaaa
leaacaWGPbaabeaaaOqaaiaadEeadaWgaaWcbaGaamyAaaqabaaaaa aa@3F13@
G
i
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbbG8FasPYRqj0=yi0dXdbba9pGe9xq=JbbG8A8frFve9
Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGhbWaaS
baaSqaaiaadMgaaeqaaaaa@3844@
τ
i