スプリングタイプ13は幾つかの独立変形モードを持つビーム要素のように機能します。
- 引張り / 圧縮
- ねじり
- 曲げ(2モード)
- せん断(2モード)
ビーム要素とは異なり、 変位(または回転)と力(またはモーメント)の間の関係は形状(断面積、長さ、および慣性モーメント)と材料定数 (ヤング率、せん断弾性係数)から計算されるのではありません。代わりに、これらは異なる剛性定式化を通してユーザー定義されます(詳しくは剛性定式化をご参照ください)。
スプリングタイプ13はその長さが0でない時だけ働きます。節点 1と2が局所X軸の定義に常に用いられます。局所 Y 軸は時刻 t=0 において定義され、それぞれのサイクルで平均の X 軸周りの回転を考慮して更新されます。初期のY 軸は複数の方法で定義できます。ビーム要素には第3節点を用いることができます。スキューフレームの局所Y軸を用いることも可能です。スキューフレームも第3節点も定義されていない場合、全体Y軸がスキューのY軸に取って代わります。Yスキュー軸が局所X軸と平行な場合、局所Y軸とZ軸は任意の位置に置かれます。そのZ-軸は最後に、X軸とY軸のベクトル積として計算されます。
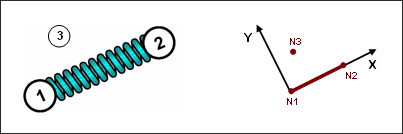
図 1. スプリングタイプ13
ビームタイプスプリングの図を以下に示します(
図 2)。
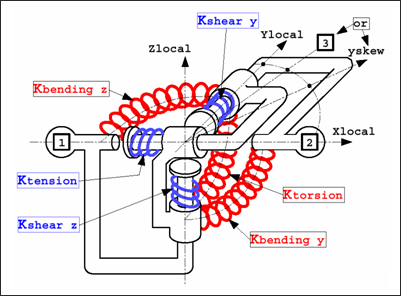
図 2. スプリングタイプ13
曲げ変形は
図 3で説明されます。この変形は、2節点の回転の差のみを考慮します。ビームの二重曲げは曲げ変形を生成しますが、せん断変形は以下に示したようになります。
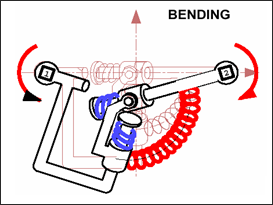
図 3. 曲げを受けるスプリングタイプ13
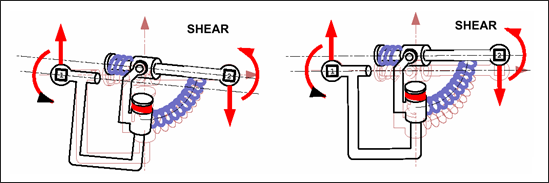
図 4. せん断-曲げを受けるスプリングタイプ13
ビームタイプスプリングは、実際のビームのように振る舞い、長さ方向の曲げモーメントの変化はせん断の増加を生成します。スプリングのせん断力は曲げモーメントの変化を含んでいます。
注: スプリングのプロパティを定義する際は、物理的な意味のある値を導入することが強く推奨されます。高いせん断剛性と曲げ剛性ゼロのスプリングは推奨されず、間違った結果を生む可能性があります。
スプリングタイプ8と異なり、スプリングタイプ13では人工的な力およびモーメントを生成することなしに剛体回転が可能です。
図 5では、剛体回転時のスプリングタイプ8および13の挙動を比較しています。

図 5. スプリングタイプ8と13の剛体移動
限界時間ステップの計算にはスプリングタイプ4と同じ式が用いられ、全ての自由度の最小値が最終的に保持されます。そのため、曲げとせん断の連成を考慮するため、曲げ剛性が修正されます:
(1)
(2)
スプリングタイプ8と13では、符号の規則が同じではないため、両者の結果を比較する場合には混乱が生ずるかもしれません。スプリングタイプ13では、変形の符号は初期長さの変化に基づきます。
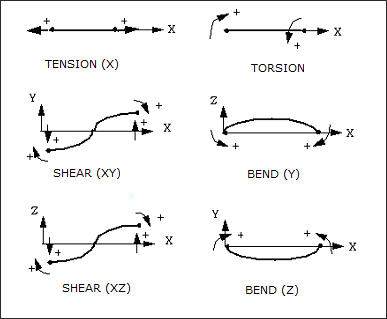
図 6. スプリングタイプ13の符号規則
スプリングが引張りを受ける場合、その変形は常に正となります(図 6)。これはスプリングタイプ8では真とは限りません。スプリングは1つ(あるいは全て)の方向で0となる事ができるため、正と負のスプリング変形は初期長さの変化として定義できません。符号の規則としては全ての自由度に対し、節点2の変位(または回転)から節点1の変位(または回転)を引いた値が正の場合(負の場合も同様)、その変形は正(負の場合も同様)となります。
図 7 は、
Radiossで適用されている符号規則の結果としての、スプリングタイプ8と13の差異を説明しています。

図 7. スプリングタイプ8と13の間の距離
詳細については、Radioss Theory Manual内のBeam Type Spring Elements (TYPE13)をご参照ください。






