スプリングTYPE12はプーリーのモデル化に用いられます。シートベルトのモデル化に用いられる時、これは3節点で定義されます。
節点2はプーリー位置に置かれ、可変形のロープが3節点に加わります(図 1)。スプリングの質量は3節点に 、節点1と3に ¼ 、節点2に ½ 分配されます。
クーロン摩擦を節点2に2つのストランドの角度を考慮して与えることができます。摩擦なしでは、力は次のように計算されます:
(1)
ここで、
-
- ロープの伸びの合計
-
- 剛性
Coulomb摩擦が用いられた場合、力は次のように計算されます:
(2)
ここで、
-
-
- 角度(単位はラジアン)
-
- fct_IDの関数fr
- Ifr =0 (対称挙動)(3)
- Ifr =1 (非対称挙動)(4)
はストランド1-2の伸び、
はストランド 2-3の伸びです。
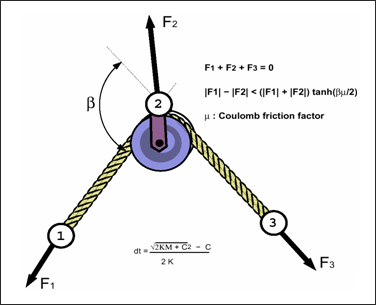
図 1. スプリングTYPE12、プーリー
時間ステップはスプリングTYPE4と同じ式で計算されますが、その剛性は、高い摩擦での安定性を保証するため2倍の値に置き換えられます。
注: 節点1または節点3が節点2までスライドしないように、2つのストランドの長さが十分である必要があります。節点1と3に結び目があると、節点1と3は節点2で停止します。
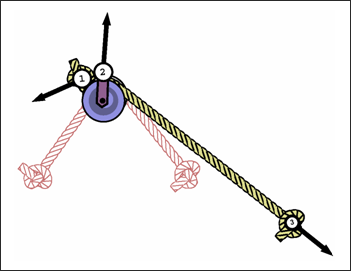
図 2. スプリングTYPE12、プーリー
詳細については、Radioss Theory Manualをご参照ください。

