運動学的ジョイントは/PROP/KJOINTで宣言されます。ジョイントは1つのスプリングと結合された物体に属する2つの局所座標軸によって定義されます。
ここで局所軸の直交性を保証するため、結合されている物体は剛体であることを仮定します。しかしながら、変形可能な物体もジョイントに結合することができます。変形の間に軸の直交性が崩れた場合、ジョイントの安定性は保証できません。
Radiossではいくつもの種類のジョイントが使用可能です。運動学的ジョイントタイプにそれらをリストします。
運動学的ジョイントタイプ
| タイプ番号 |
ジョイントタイプ |
dx |
dy |
dz |
x |
y |
z |
| 1 |
球 |
x |
x |
x |
0 |
0 |
0 |
| 2 |
回転 |
x |
x |
x |
0 |
x |
x |
| 3 |
円筒 |
0 |
x |
x |
0 |
x |
x |
| 4 |
平面 |
x |
0 |
0 |
0 |
x |
x |
| 5 |
ユニバーサル |
x |
x |
x |
x |
0 |
0 |
| 6 |
並進 |
0 |
x |
x |
x |
x |
x |
| 7 |
オールダム |
x |
0 |
0 |
x |
x |
x |
| 8 |
剛性 |
x |
x |
x |
x |
x |
x |
| 9 |
フリー |
0 |
0 |
0 |
0 |
0 |
0 |
x: 固定自由度を示します。
0: フリー自由度(ユーザー定義)を示します。
ジョイントのプロパティは2つの結合された座標系に関して計算された局所座標系で定義されます。これらは最初の時点で一致している必要はありません。局所座標軸の初期位置が常に一致する場合は、ジョイントの局所フレームは平均位置に定義されます。次にその局所座標系はこれらの回転軸に関して計算されます。
6つのジョイント自由度があります:
および
の4つのパラメータのみを指定して使用できます。これらは局所スキューフレームで計算されます。
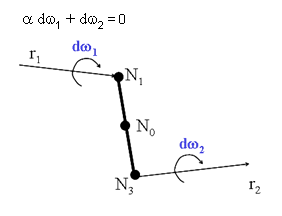
図 1. 運動学的ジョイントの定義
各ジョイントタイプでは、固定自由度とフリー自由度を区別します。固定自由度には剛性が一定しているという特徴があります。フリー自由度の剛性には大きい値を選択することを推奨します。フリー自由度では、ユーザー定義の特徴(線形または非線形弾性の場合がある)に臨界前粘性減衰を組み合わせます。
並進および回転自由度は次のように定義されます:
(1)
ここで、
と
は局所座標系における2つのジョイント節点の全変位です。
(2)
ここで
と
は局所ジョイント座標フレームに関する2つの結合された物体の全相対回転です。

図 2. 運動学的ジョイントの概要図
力とモーメントの計算
方向
の力は次のように計算されます:
- 線形スプリング:
-
:並進剛性(Ktx、KtyおよびKtz)
-
:並進粘度(Ctx、CtyおよびCtz)
- 非線形スプリング:
方向
のモーメントは次のように計算されます:
- 線形スプリング:
-
:回転剛性(Krx、Kry、Krz)
-
:回転粘度(Crx、Cry、Crz)
- 非線形スプリング:
ジョイントの長さは0にすることもできます。球面ジョイントやユニバーサルジョイントの定義には長さ0のスプリングを用いることを推奨します。一般的なケースでのモーメントの全体での釣り合いを満足するため、回転自由度の補正項が次のように計算されます:
(3)
(4)
(5)
ジョイントはユーザー定義の質量や慣性をもつことができません、このため節点時間ステップが常に用いられます。

