RD-E:3900 バイオメディカルバルブ
流体構造連成相互作用(FSI)問題が検討されます。Radioss ALE/CFDソルバーがこの問題を解くのに用いられます。
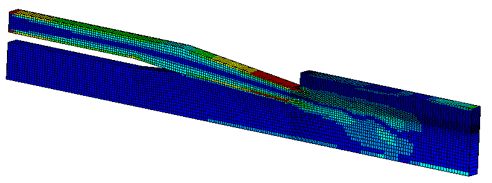
図 1.
- FSIケーススタディをどのようにセットアップするか
- ALE/CFDの実行に用いられている様々なオプションの簡潔な記述(詳細についてはRadiossTheory Manualを参照のこと)
使用されるオプションとキーワード
- FSI、CFD、流体
- 流入と流出
- 乱流流れ
- /MAT/LAW11(BOUND)
- /ALE/MAT
- /ALE/BCS
- /PROP/TYPE14(FLUID)
- /VEL/ALE(廃止)
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
単純化された心臓バルブがモデル化されます。バルブは流入する血液の流れの圧力の下で開きます。バルブの開くプロセスが考慮され、問題は非定常です。
加えて、流体-構造連成相互作用が血液の圧力の下でのフラップの変形として考慮される必要があります。
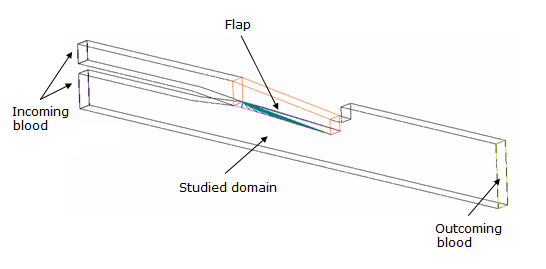
図 2. 問題の定義
モデリング手法
準-均一なソリッドメッシュが領域の離散化に用いられます。軸に沿って十分に細かいメッシュの厚さ方向の1要素が用いられます。
シェル要素がフラップのモデル化に用いられます。フラップは1つの側が固定されその節点には固定するスプリングが付けられます。それぞれの端部には1列のメッシュが生成され流入と流出が定義されます。
問題は非圧縮で、そのため、時間ステップを増加させるために、流体内の音速を恣意的に50 m/sに下げました。
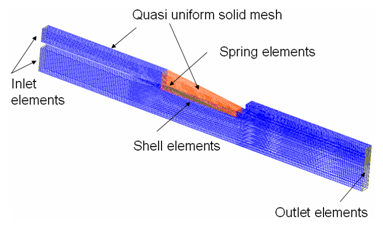
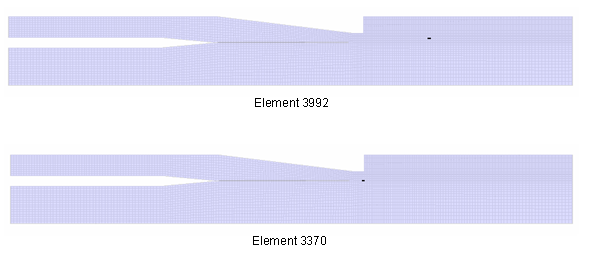
図 3. モデルのメッシュ
- フラップのための線形弾性材料則(/MAT/ELAST)
- モデルの主要な部分のための乱流材料(/MAT/LES_FLUID)
- 材料特性
- Rho
- 960.0
- 音速
- 50.0
- 分子の運動学的粘性
- 5.45E-05
- サブグリッドスケールモデルフラグ
- 0
- Cs
- 0.1
- Csp
- 0.1
- 流入で流体の密度、エネルギーと圧力を定義する流体材料(/MAT/BOUND)
- 材料特性
- Rho
- 960.0
- Ityp
- 2(一般ケース)
- 音速
- 50.0
- 流出で領域外部の流体圧力を定義する流体材料(/MAT/BOUND)
- 材料特性
- Rho
- 960.0
- Ityp
- 3の場合、サイレント境界(NRF)
- 音速
- 50.0
- 特性長さ
- 1.0E-03 m
フォーマット/ALE/MATがそれぞれの流体材料に割り当てられます。
- 上側の流入
- Vx= 1.253
- 下側の流入
- Vx= 0.849
| タイプ | 位置 | 境界条件 | |
|---|---|---|---|
| 1 | /BCS | 水平節点 | 並進 Vz = 0 |
| 2 | /ALE/BCS | 水平節点 | グリッド速度 Wz = 0 |
| 3 | /BCS | フラップの横方向エッジの領域の節点 | 並進 Vz = 0 |
| 4 | /ALE/BCS | フラップの横方向エッジの領域の節点 | Wx = Vx Wy = Vy Wz = Vz |
| 5 | /BCS | フラップの節点 | 並進 Vz = 0 回転 Wx = 0 回転 Wy = 0 |
| 6 | /ALE/BCS | フラップの節点 | Wx = Vx Wy = Vy Wz = Vz |
インターフェースTYPE2が生成され、フラップの横方向エッジの流体領域の節点がフラップのLagrangeメッシュに結合されます。こうして、流体領域が構造のパートに結合されます。
この方法を用いて、流体と構造の間で異なるメッシュとメッシュ密度を持つことが可能になります。
Radioss ALE/CFD専門用語
Euler定式化
Eulerian定式化は流体力学において古典的な表現です。メッシュは固定され、材料がメッシュの中を流れます。方程式は対流項を考慮するため、Lagrange定式化に関して修正されます。
これは材料データでのフラグにより、特定のパートに対してアクティブ化されます。
/EULER/MAT/mat_ID
- mat_ID
- Euler定式化がセットされる材料のID
このケースでは、領域の境界(と主にフラップ)が動くため、Euler定式化は用いることができません。
ALE(Arbitrary Lagrangian Eulerian)定式化
材料は任意に移動するメッシュ内を流れ、これは LagrangeまたはEuler定式化に縮退させることができます。
これは材料データでのフラグにより、特定のパートに対してアクティブ化されます。
/ALE/MAT/mat_ID
- mat_ID
- ALE定式化がセットされる材料のID
グリッド速度と変位は任意です。
実際、ビルトインのアルゴリズムでALE領域境界の変位に基づいてスムーズなグリッド変形が決められます。いくつかのアルゴリズムを使用可能であり(DONEA、SPRINGS、DISP、およびZERO)、この場合はDISPオプションが用いられます。節点の速度は結合された節点の平均速度を用いて計算されます。
ALE材料とLagrangian材料の間の境界節点はLagrangianに設定される必要があります:グリッドと材料の速度は同じです。ALEとEuler材料の間の境界節点はグリッド速度が固定される必要があります。
両方の条件は/ALE/BCSオプションを用いて設定します。
ALE節点に拡張された境界条件を指定(グリッド速度成分を0または材料速度に指定)したり、またはグリッド速度成分を課したり、ALEリンクを任意の節点に対して古典的な運動条件と同様の方法で指定したりすることが可能です。
節点境界条件
- 滑りありと無しの境界条件
- 強制速度(流入における強制流束など)
- 剛結(リスタート時の一時追加)
- 剛な構造をモデル化する剛体と結合と更に抗力と揚力の計算(すなわち、剛体上の流体の力積を時刻歴データベースに保存)。
- 滑り無しと完全滑りのグリッド条件
- Lagrange条件、即ち、グリッドと材料の速度は等しいものとして設定
- 節点の通常の分布を維持するALE リンク
- 強制グリッド速度(移動する流入と流出など)
基本境界条件
- ユーザー関数による強制変化条件
- 連続性
- 事前定義の関数によるスムーズな変化
サイレント境界(NRF)(材料LAW11、オプション3)は圧力と境界場の自由インピーダンスの場を保証します。
Radioss ALE/CFDでは、上のオプションのどのような組み合わせでも指定できます。一方、様々な対流と拡散方程式のクロージャについては、慎重に検証される必要があります。
- 流入、流束が強制速度を用いて課されます。密度、エネルギー、乱流エネルギー(即ち、 k)は一定とします。連続条件が圧力(表示目的のみ)とイプシロンに対して課されます。乱流エネルギー、rho kは外部流れに対しては0に、内部流れに対しては1.5*rho*(0.06 Vin)2に設定します。
- 流出、圧力を除いた全ての変数に対する連続条件が課されます。サイレント境界NRFオプションが用いられた時は、 ユーザーが音速の値と代表的な緩和の長さを与え、これは興味の最大波長よりも大きい必要があります。
- 側面、サイレント境界NRFオプションまたは境界要素無しの滑り条件による全ての変数の連続条件。
要素が境界に存在しない場合連続性が仮定されますが、流束を許さないために運動条件は必要です、そうでないと対流方程式が完結せず、プログラムは発散する可能性があります。
結果
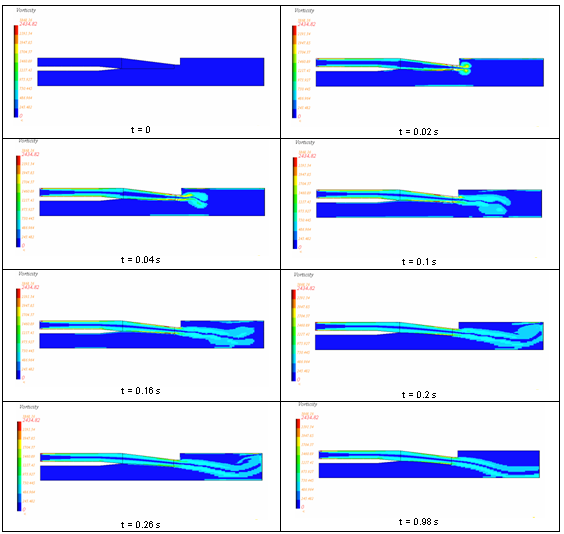
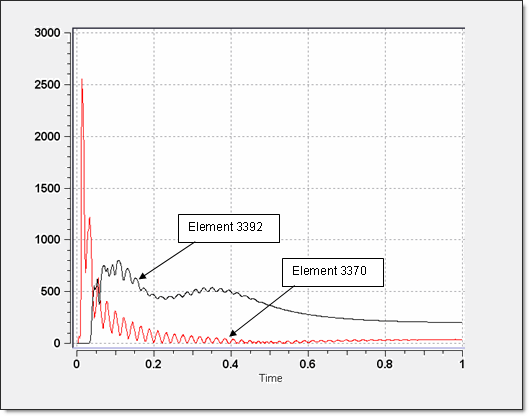
図 4. 時間と空間での速度分布
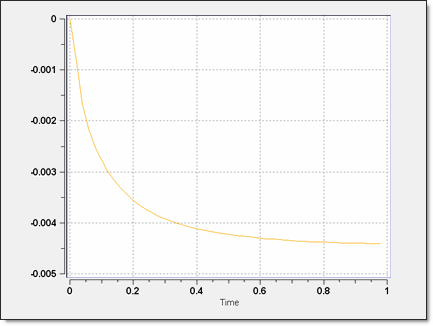
図 5. フラップの自由端(節点23360)のメートルでの鉛直変位
まとめ
この例題はRadiossの流体-構造連成相互作用のシミュレーション能力を示しています。LagrangieメッシュにつけられたALE定式化の使用が記述されています。Radioss ALE/CFDに関するいくつかの基本的な解説がされています。