RD-E:4300 多項式EOSを用いた理想気体のモデル化
この例題の目的は、数値的圧力、内部エネルギー、理想気体材料則の音速をプロットすることにあります。
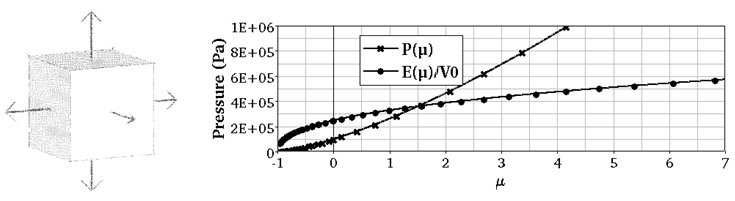
図 1.
これらの定式化の出力を理論解と比較するため圧縮 / 膨張の単純なテストが行われます。
使用されるオプションとキーワード
- 理想気体
- 多項式 EOS(/EOS/POLYNOMIAL)
- 絶対 / 相対定式化
- 圧力シフト
- 流体材料(/MAT/LAW6 (HYDROまたはHYD_VISC))
- 強制変位(/IMPDISP)
- Lagrangian境界条件(/ALE/BCS)
- それぞれの面の節点は強制変位で移動されます(/IMPDISP)
- 要素圧力、密度と内部エネルギー密度は、時刻歴応答ファイルに保存されます。
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
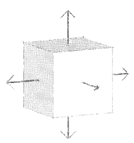
図 2.
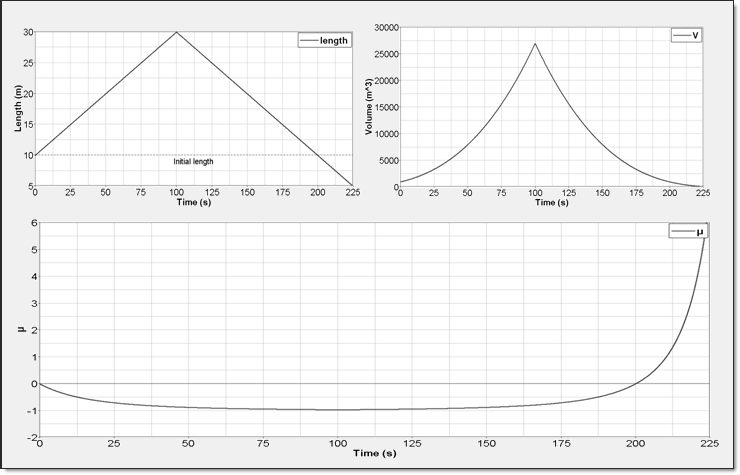
流体は理想気体と仮定します。体積は純圧縮とそれに続く膨張 (図 3)を考慮するために3方向に変化させます。
このテストは1つのALE要素(8節点ソリッド)と多項式EOSでモデル化されます。
圧力、内部エネルギーと音速の変化が数値計算出力と理論解の間で比較されます。
シミュレーションの反復
1つのALEソリッド要素が用いられます。材料は、ソリッドの節点がLagrangeであると定義することにより要素内に閉じ込められます。それぞれの面に対して、4節点に強制変位が法線方向に与えられます。
多項式 EOS
- 非圧縮性気体
- 線形弾性材料
- 理想気体
この例題は理想気体のモデル化のみに焦点を当てます。
結果
理論解
- 圧力:理想気体の圧力は以下で与えられます:
(5) したがって:(6) Radiossは内部エネルギー変化の計算に等エントロピー過程の仮説を仮定します:(7) この理論は以下の微分方程式を与えます:(8) これはという形式を持ち、一般解は次のとおりです:(9) 圧力はポリトロープな状態にもあります:(10) (11) ここで、 は材料定数です(熱容量の比)。原子の気体では、 =1.4。空気は主に2原子の気体からなるので、通常空気のガンマは1.4に設定します。
- 内部エネルギー:
- 音速: 理想気体の音速は:
(13) 式 11 は体積に関する表現を与えます:(14)
| 圧力(Pa) | 内部エネルギー密度(J) | 音速(m/s) | |||
|---|---|---|---|---|---|
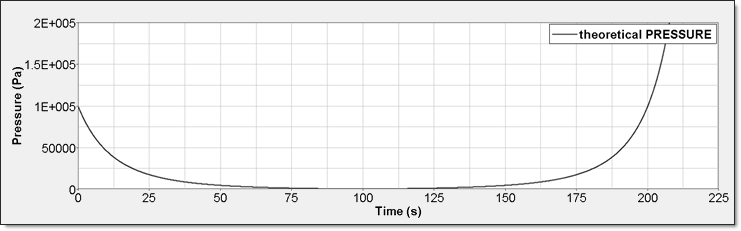
図 4. 理想気体圧力
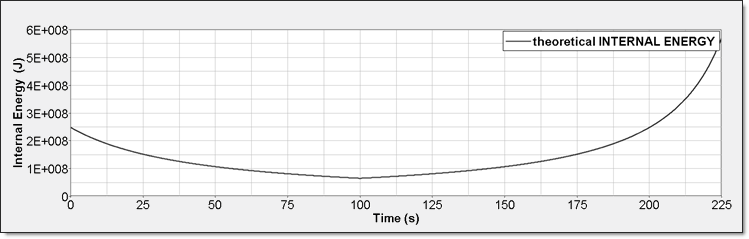
図 5. 理想気体内部エネルギー
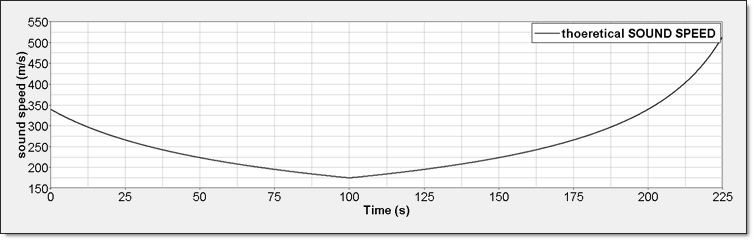
図 6. 理想気体音速
材料コントロールカード
| ケース | 数学的モデリング | 圧力 | エネルギー |
|---|---|---|---|
| 1 | 絶対値 | 絶対値 | |
| 2 | 相対値 | 絶対値 | |
| 3 | 相対値 | 相対値 | |
| 4 | 絶対値 | 相対値 |
音速と時間ステップ
| ケース | C0 | C1 | C4 | C5 | c2 以下より: 式 25 |
理論値との比較 |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | ||||
| 2 | 0 | 0 | ||||
| 3 | ||||||
| 4 |
それぞれの4つの定式化に対して、Radiossにより計算された音速は理論値と一致しています。時間ステップとサイクル数は影響されません。
ケース 1:圧力とエネルギーの両方が絶対値
- 圧力:状態方程式
(30) ここで、
多項式の係数を特定すると以下が導かれます:(31) ここで、
- 対応する入力:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Absolute Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 0 0 /EOS/POLYNOMIAL/1 Polynomial EOS-Absolute Pressure-Absolute Energy # C0 C1 C2 C3 0 0 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 250000 0 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - 結果の出力:
表 4. 時刻歴応答 寸法 初期値 Unit /TH/BRICK () 圧力 /TH (IE) エネルギー /TH/BRICK (IE) 圧力 - 理論界との比較理想気体圧力の数値解析結果は、時刻歴で与えられます。要素時刻歴(/TH/BRICK)でこれを表示できます。この結果を理論解と比較します。曲線は重ねて示されます。
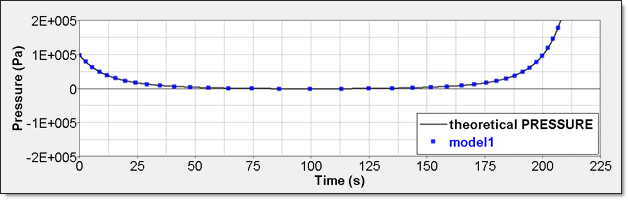
図 7. 数値的圧力、モデル1内部エネルギーは2つの異なる方法で得ることができます。1つ目は、要素時刻歴(/TH/BRICK)に記録された内部エネルギー密度()です。2つ目は、全体の時刻歴からの内部エネルギーで、これは、モデルが単一要素であるためです。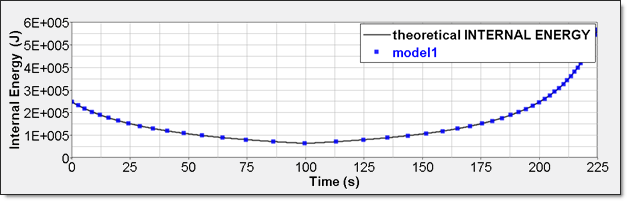
図 8. 数値的内部エネルギー、モデル1
ケース 2:圧力が相対値でエネルギーが絶対値
- 圧力:状態方程式
(32) 相対圧力:(33) 多項式の係数を特定すると以下が導かれます:(34) ここで、
最小圧力:(35) のため、最小圧力は0以外の値に設定される必要があります。
- 対応する入力:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Relative Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 1.5256E-5 -100000 /EOS/POLYNOMIAL/1 Polynomial EOS-Relative Pressure-Absolute Energy # C0 C1 C2 C3 0 0 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 250000 100000 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - 結果の出力:
時刻歴応答 寸法 初期値 Unit /TH/BRICK () 0 圧力 /TH (IE) エネルギー /TH/BRICK (IE) 圧力 - 理論界との比較
理想気体圧力の数値解析結果は、時刻歴で与えられます。要素時刻歴(/TH/BRICK)でこれを表示できます。この結果を理論解と比較します。曲線は重ねて示されます。
要素時刻歴(/TH/BRICK)は、Pshに対する相対圧力です。結果の曲線は、Psh値でシフトされ、0から開始します。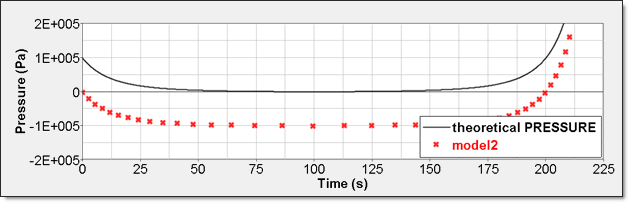
図 9. 数値的圧力、モデル2内部エネルギーは2つの異なる方法で得ることができます。1つ目は、要素時刻歴(/TH/BRICK)に記録された内部エネルギー密度()です。2つ目は、全体の時刻歴からの内部エネルギーで、これは、モデルが単一要素であるためです。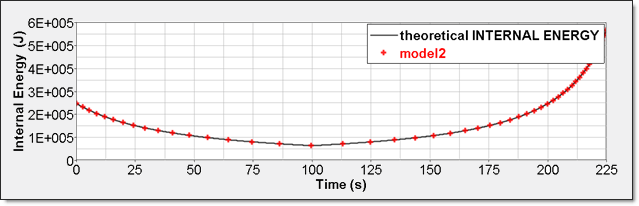
図 10. 数値的内部エネルギー、モデル2
ケース 3:圧力とエネルギーの両方が相対値
- 圧力:状態方程式
(36) 初期内部エネルギーを導入することができます:(37) 参照値からの圧力は以下を与えます:(38) ここで、。
多項式の係数を特定すると以下が導かれます:(39) ここで、、、および。
最小圧力:(40) のため、最小圧力は0以外の値に設定される必要があります。
- 対応する入力:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Relative Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 1.5256E-5 -100000 /EOS/POLYNOMIAL/1 Polynomial EOS-Relative Pressure-Absolute Energy # C0 C1 C2 C3 100000 100000 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 0 100000 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - 結果の出力:
時刻歴応答 寸法 初期値 Unit /TH/BRICK () 0 圧力 /TH (IE) 0 エネルギー /TH/BRICK (IE) 0 圧力 - 理論界との比較
理想気体圧力の数値解析結果は、時刻歴で与えられます。要素時刻歴(/TH/BRICK)でこれを表示できます。この結果を理論解と比較します。曲線は重ねて示されます。
要素時刻歴(/TH/BRICK)は、Pshに対する相対圧力です。結果の曲線は、Psh値でシフトされ、0から開始します。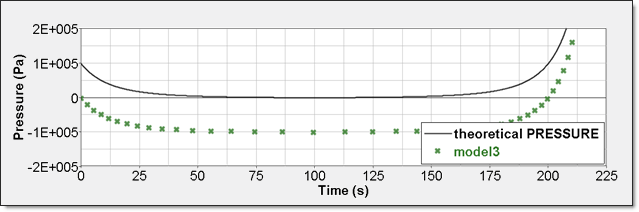
図 11. 数値的圧力、モデル3内部エネルギーは2つの異なる方法で得ることができます。1つ目は、要素時刻歴(/TH/BRICK)に記録された内部エネルギー密度()です。2つ目は、全体の時刻歴からの内部エネルギーで、これは、モデルが単一要素であるためです。数値解析結果の内部エネルギーは初期エネルギーからの相対値で、絶対値から値だけシフトされ、0から開始します。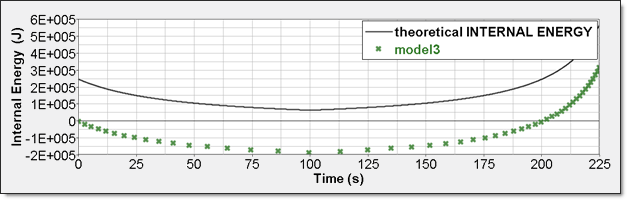
図 12. 数値的内部エネルギー、モデル3
ケース 4:圧力が絶対値でエネルギーが相対値
- 圧力:状態方程式
(41) 初期内部エネルギーを導入することができます:(42) 与えられた参照値からの圧力:(43) 多項式の係数を特定すると以下が導かれます:(44) ここで;
- 対応する入力:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| /MAT/HYD_VISC/1 Polynomial EOS-Relative Pressure-Absolute Energy # RHO_I RHO_0 1.204 0 # Knu Pmin 1.5256E-5 0 /EOS/POLYNOMIAL/1 Polynomial EOS-Relative Pressure-Absolute Energy # C0 C1 C2 C3 100000 100000 0 0 # C4 C5 E0 Psh RHO_0 .4 .4 0 0 1.204 #---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----| - 結果の出力:
時刻歴応答 寸法 初期値 Unit /TH/BRICK () 圧力 /TH (IE) 0 エネルギー /TH/BRICK (IE) 0 圧力 - 理論界との比較要素時刻歴(/TH/BRICK)は、絶対圧力を与えます。この結果を理論解と比較します。曲線は重ねて示されます。
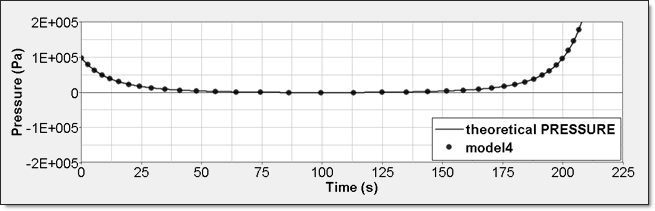
図 13. 数値的圧力、モデル4内部エネルギーは2つの異なる方法で得ることができます。1つ目は、要素時刻歴(/TH/BRICK)に記録された内部エネルギー密度()です。2つ目は、全体の時刻歴からの内部エネルギーで、これは、モデルが単一要素であるためです。数値解析結果の内部エネルギーは初期エネルギーからの相対値で、絶対値から値だけシフトされ、0から開始します。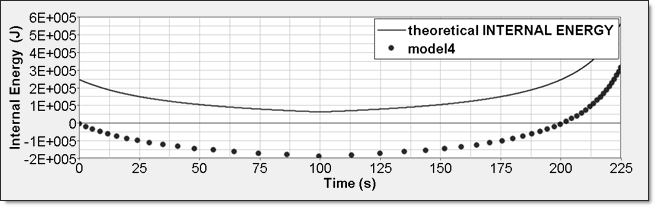
図 14. 数値的内部エネルギー、モデル4