RD-E:4200 ゴムのリング: クラッシュとスライドの例題
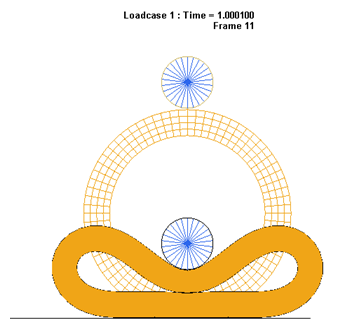
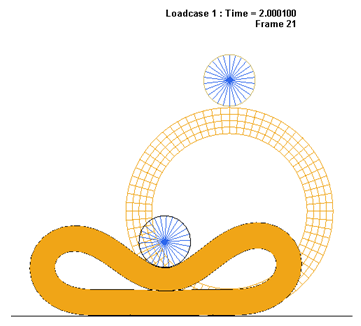
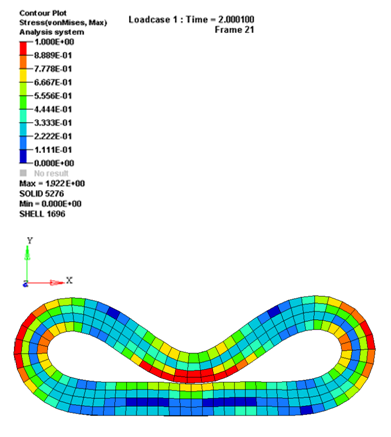
平らで剛な平面上に静止するゴムのリングが円形のローラーで押し下げられリング内部に自己接触を起こします。次に、押し潰されたリングが平らなサーフェスに沿って転がるようにローラーは同時に平行移動と回転移動します。
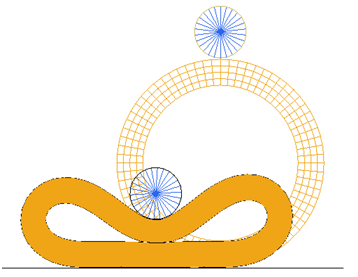
図 1.
この例題は静的問題として考慮され、非線形陰解法ソルバーが用いられます。
使用されるオプションとキーワード
- 非線形陰解法大変位解析
- 自己接触
- 超弾性材料
- 超弾性ゴム材料(/MAT/LAW42 (OGDEN))
- 境界条件(/BCS)
- 自由度の解放(/BCSR)
- 強制変位(/IMPDISP)
- 非圧縮性ソリッド要素(/PROP/TYPE14(SOLID))
- 接触定義(/INTER/TYPE7)
- 陰解法解析(陰解法コントロール)
- 非線形陰解法パラメータ
- 陰解法タイプ
- 静的非線形
- 非線形ソルバー
- BFGS準-Newton 法
- 終了の条件
- エネルギーの相対残差
- 収束判定基準
- 0.001
- 剛性マトリックスの更新
- 最大5回の反復
- 時間ステップコントロール法
- 孤長
- 初期時間ステップ
- 0.001
- 最小時間ステップ
- 1e-6
- 最大時間ステップ
- 0.001
- ラインサーチ法
- 自動
- 接触インターフェースがある場合の特別な残差力の計算:
- 5
- 望ましい収束の反復回数
- 6
- 収束の最大反復回数
- 15
- 時間ステップ減少係数
- 0.8
- 最大時間ステップ増加係数
- 1.1
- 孤長
- 自動計算
- スプリングバックオプション
- なし
- 線形陰解法オプション
- 線形ソルバー
- 直接法
- 前処理法
- 分解された近似逆行列
- 最大反復回数
- 系の次元(NDOF)
- 終了基準
- 前処理したマトリックスの相対残差
- 終了基準の収束判定
- マシンの精度
第2の荷重ステップのためにリスタート解析が実行されます。
/IMPL/PRINT/NONLIN/-1 --- Printout frequency for nonlinear iteration
/IMPL/NONLIN/2 ---- Static nonlinear computation
5 1 0.001
/IMPL/SOLVER/3 ----- Solver method (solve Ax=b)
5 0 3 0.0
/IMPL/DTINI ----- Initial time step determines initial loading increment
0.001
/IMPL/DT/STOP ------- Min Max values for time step
1e-6 0.001
/IMPL/DT/2 ------ Time step control method 2 - Arc-length + Line-search will be used with this method to accelerate and control convergence.
6 0 15 0.8 1.1
/IMPL/AUTOSPC/ALL ---- Constraining automatically zero stiffness dof
/IMPL/LSEARCH/3 ---- Line search method for nonlinear analysis
/IMPL/RREF/INTER/5 ------ Special Reference residual computation with contact陰解法オプションの詳細についてはRadiossマニュアルを参照してください。
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
この例題の目的は、Radiossを用いた超弾性材料と接触を含む非線形大変位陰解法解析を示すことにあります。
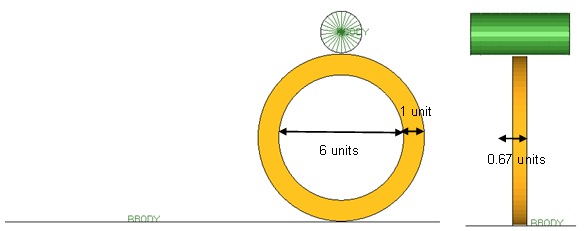
図 2. ゴムのリングとローラーモデルの形状
- 材料特性
- 0.7
- -0.5
- 2.0
- 2.0
- ポアソン比
- 0.495
- 材料特性
- 密度
- 7.9e-9
- ヤング率
- 600
- ポアソン比
- 0.3
幾何学的線形(NLSTAT)または幾何学的非線形(NLGEOM)解析
幾何学的線形解析では全ての変形と回転は小さいとします。変位量がモデルの寸法の5%程度であれば小さいと考えられます。
このゴムのリングの例題では、押しつぶされた後の最終変形とひずみが上の限度よりはるかに大きくなります。したがって、幾何学的線形NLSTAT解析をこの例題のために検討することはできません。
モデリング手法
- メッシュとプロパティリングのメッシュは規則的なソリッドメッシュで、幅方向に4要素(0.25 単位の寸法)で厚さ方向が2要素(0.335 単位の寸法)でモデル化されています。平らで剛なサーフェスと円形のローラーはどちらも規則的な板厚0.01mmのシェルメッシュで平らなサーフェスはおよそ0.75単位の寸法で、ローラーはおよそ0.467単位の寸法でモデル化されています。
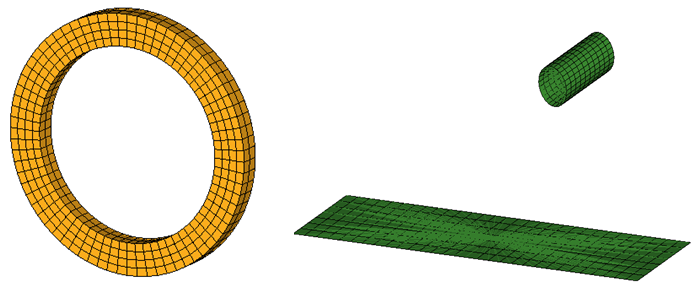
図 3. ゴムのリングとローラーモデルの形状リングは1次の完全積分ソリッド要素を用いてモデル化されました。/PROP/SOLID/5 WHEEL 14 10 1 222平らなサーフェスとローラーは1次の低減積分シェルを用いて板厚方向3積分点でモデル化されました。バリアの詳細なポスト処理は必要ないため、完全積分要素は考慮されませんでした。/PROP/SHELL/6 BARRIER 1 2 3 0.01 - 荷重および境界条件ゴムのリングに作用する境界条件はステップ1では図 4に示したように与えられます。
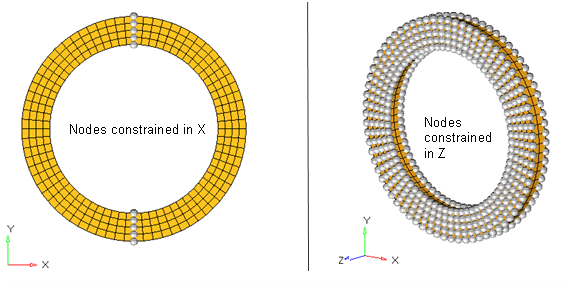
図 4. ステップ1でリングに作用する境界条件平らで剛なサーフェスと円形のローラーに作用する境界条件はステップ1では図 5に示したように与えられます。
リングの内面で自己接触が起きるようにローラーが6.22単位Y 軸方向に押し下げられる間、平らなサーフェスは全ての自由度が拘束されます。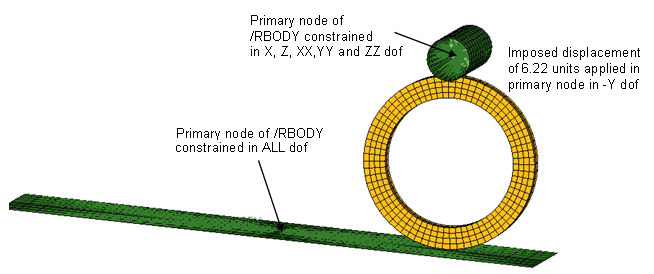
図 5. ステップ1で平らなサーフェスとローラーに作用する境界条件ステップ2では、押しつぶされた形状の輪が平らで剛なサーフェスのX上をX-方向に転がるように、上部ローラーが同時に並進移動と回転移動します。したがって、円形のローラーのX並進とZZ回転は、/RBODYのマスター節点から解放される必要があります。加えて、拘束されていたリングの中心節点のX自由度(図 4)を、リングが平らなサーフェスに沿って転がるように解放する必要があります。したがって、ステップ2のEngineファイルは、上で述べた自由度の解放を表す、以下のカードを持ちます。/BCSR/TRA/X/ 5 6 8 9 15 16 17 18 87 88 89 93 94 95 241 242 243 244 245 246 5717 5699 5681 5663 5662 5537 5517 5497 5477 5476 2269 /BCSR/ROT/Z 2269 - 接触定義
複数の接触が定義されています。(i)円形のローラーとゴムのリングの間の接触、(ii)平らで剛なサーフェスとゴムのリングの間の接触、および(iii)ゴムのリングの内面の自己接触です。
小さな物理ギャップ(0.05単位)が円形のローラーとゴムのリングの間とゴムのリングと平らで剛なサーフェスの間にも導入されました。接触のために指定された最小ギャップは接触を考慮に入れるために物理ギャップよりも若干大きい値が指定されました。全てのインターフェースで静的coulomb摩擦0.5が定義されています。この様な1つのインターフェースの定義を下に示します:/INTER/TYPE7/14 TOP_Rubber 25 30 4 0 0.5 0.055 000 0 0 2また、剛なパートと非常に柔らかい超弾性材料の間の接触が含まれるため、剛なパートのE*h(ヤング率 * 板厚)をゴム材料の体積弾性係数と同じオーダーにすることが推奨されます。