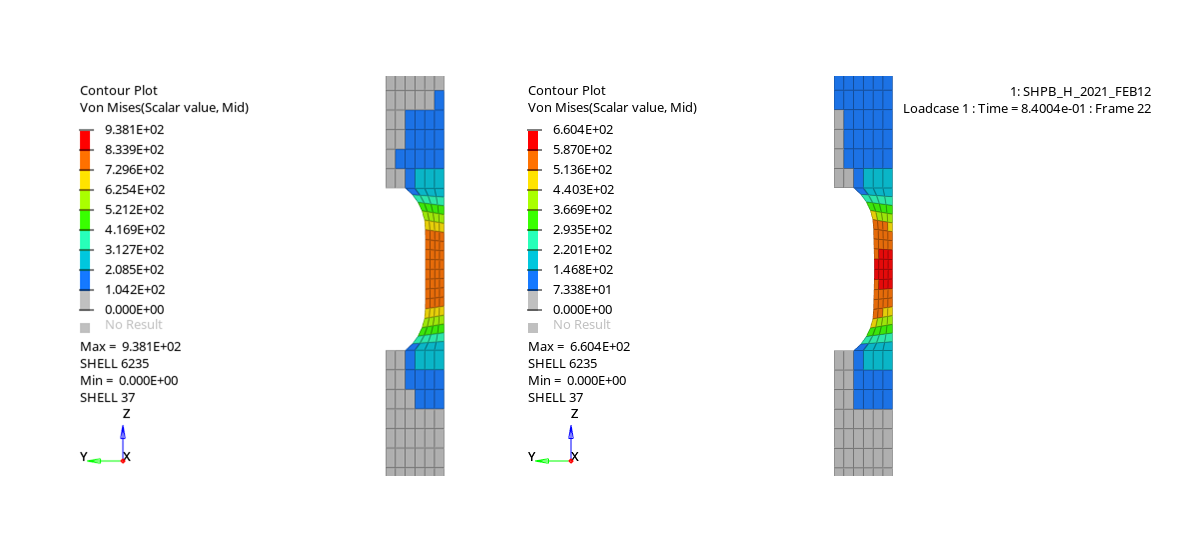
この例の目的は、衝撃時の材料に対する非常に高いひずみ速度の応答をモデル化して予測することです。
Split-Hopkinson圧力バーは、高いひずみ速度で実験を行うのに適した方法です。
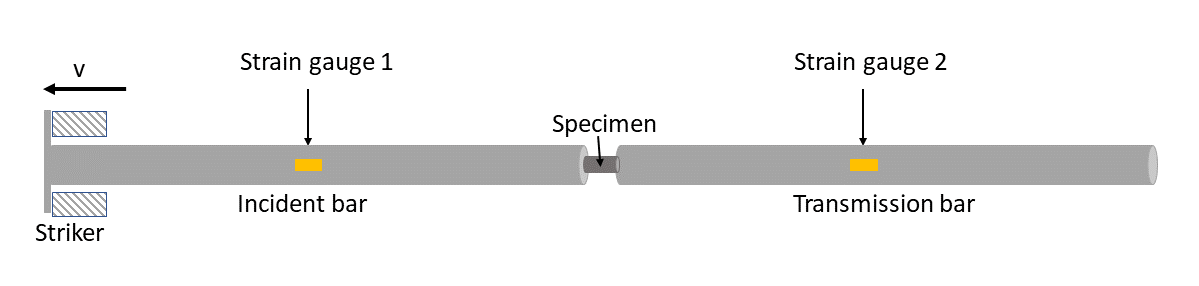
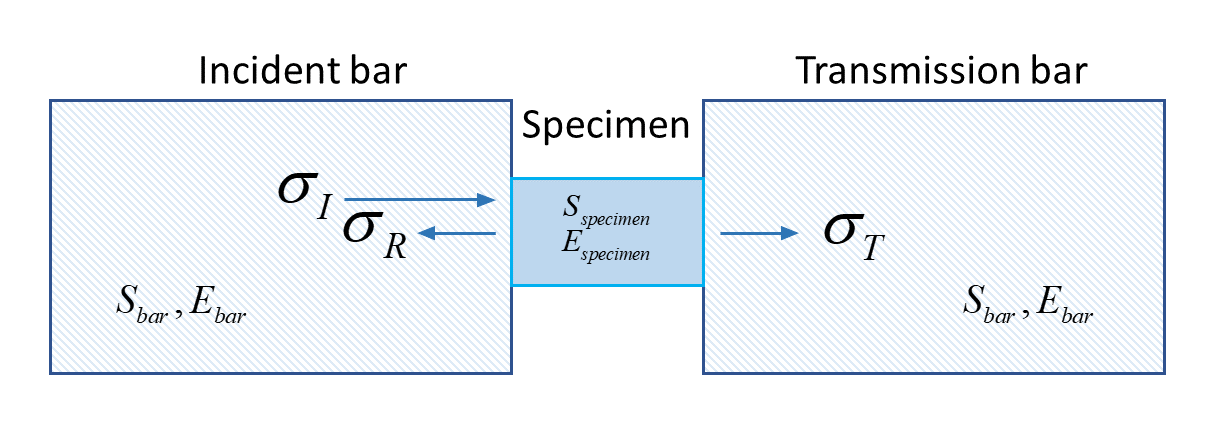
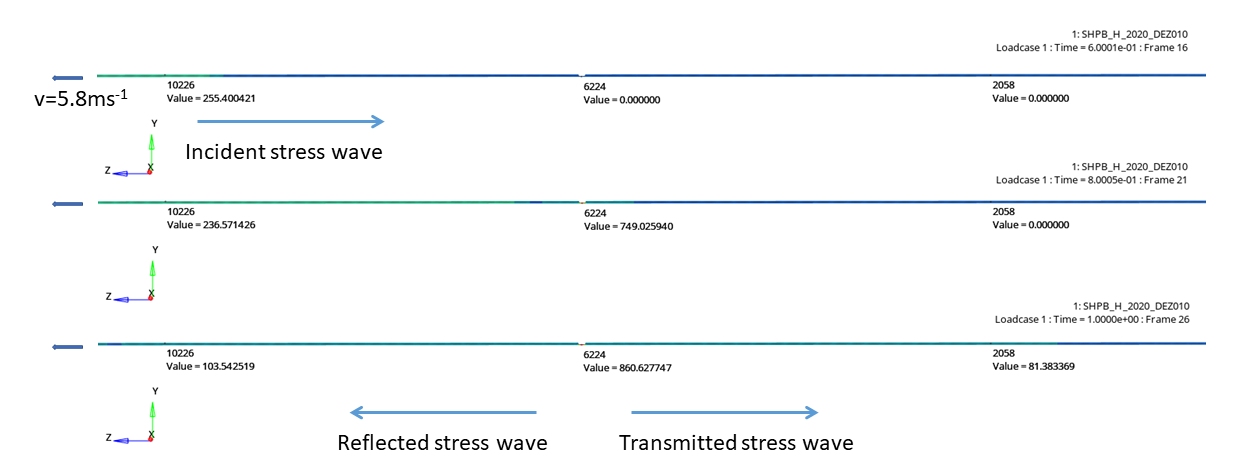
図 3 は、以下で構成される主要な試験のセットアップを示しています:
同じ長さのインシデントバーとトランスミッションバーがあり、その間に試験体が挟み込まれています。
インシデントバーの外端にストライカーが取り付けられています。スチールの飛翔体がストライカーに当たると、応力パルスがインシデントバーに導入されます。
図 3. Split-Hopkinson圧力バー装置
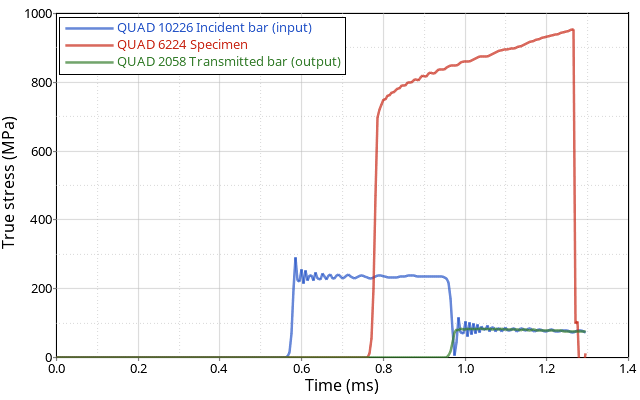
衝撃によって発生したひずみ(引張)波がインシデントバーを伝播し、ひずみゲージ1によって検出されます。波の一部は反射し、一部は試験体の接合部分を通して伝達されます。そのようにして、応力パルスは試験体内部を通り抜けてトランスミッションバーに入ります。ひずみ波信号を検出するために、インシデントバーとトランスミッションバーにひずみゲージ1とひずみゲージ2が取り付けられています。サンプル内部での反射波が試験の間の応力を均一化することを可能にします。出力または伝達される応力波に伴うひずみが出力または伝達バーのひずみゲージにより測定されます。試験体の測定長さに取り付けられたひずみゲージで実験の間の試験体の真ひずみと真塑性ひずみを直接測定します。伝達される弾性波が試験体接合部への直接の力の測定を、以下の関係式の方法によりもたらします。
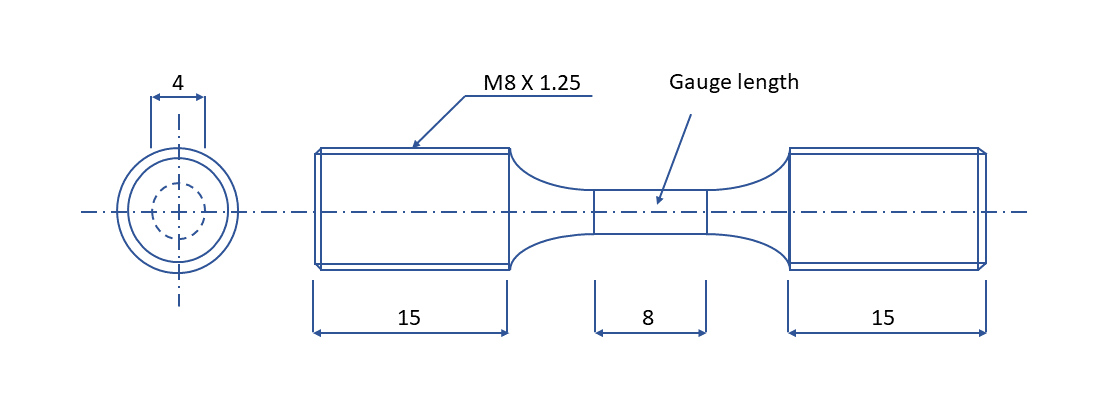
図 4. 試験体形状と断面(寸法はmm)
(1)
F
(
t
)
=
S
b
a
r
⋅
E
b
a
r
⋅
ε
T
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbWaae
WaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0Jaam4uamaaBaaaleaa
caWGIbGaamyyaiaadkhaaeqaaOGaeyyXICTaamyramaaBaaaleaaca
WGIbGaamyyaiaadkhaaeqaaOGaeyyXICTaeqyTdu2aaSbaaSqaaiaa
dsfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaaaaa@4D1D@
ここで、
E
b
a
r
出力バーの弾性係数。
ε
T
出力応力波でのひずみ。
S
b
a
r
出力バーの断面積
2つのバーが弾性を保ち、波動の消散が無視できる場合、測定される応力パルスは試験体に作用するものと同じと仮定できます。
試験体内の公称応力値は、波動の解析により、伝達される波動を用いて決めることができます:
(2)
σ
e n g i n e e r i n g
(
t
) =
F (
t
)
S
s p e c i m e n
=
S
b a r
E
b a r
S
s p e c i m e n
ε
T
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHdpWCda
WgaaWcbaGaamyzaiaad6gacaWGNbGaamyAaiaad6gacaWGLbGaamyz
aiaadkhacaWGPbGaamOBaiaadEgaaeqaaOWaaeWaaeaacaWG0baaca
GLOaGaayzkaaGaeyypa0ZaaSaaaeaacaWGgbWaaeWaaeaacaWG0baa
caGLOaGaayzkaaaabaGaam4uamaaBaaaleaacaWGZbGaamiCaiaadw
gacaWGJbGaamyAaiaad2gacaWGLbGaamOBaaqabaaaaOGaeyypa0Za
aSaaaeaacaWGtbWaaSbaaSqaaiaadkgacaWGHbGaamOCaaqabaGcca
WGfbWaaSbaaSqaaiaadkgacaWGHbGaamOCaaqabaaakeaacaWGtbWa
aSbaaSqaaiaadohacaWGWbGaamyzaiaadogacaWGPbGaamyBaiaadw
gacaWGUbaabeaaaaGccqaH1oqzdaWgaaWcbaGaamivaaqabaGcdaqa
daqaaiaadshaaiaawIcacaGLPaaaaaa@6980@
公称応力はインシデントに作用する反射波と伝達波での力の平均からも得られ、次の式で示されます:
(3)
σ
e n g i n e e r i n g
(
t
) =
S
b a r
E
b a r
2
S
s p e c i m e n
[
ε
l
(
t
) +
ε
R
(
t
) +
ε
T
(
t
) ]
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHdpWCda
WgaaWcbaGaamyzaiaad6gacaWGNbGaamyAaiaad6gacaWGLbGaamyz
aiaadkhacaWGPbGaamOBaiaadEgaaeqaaOWaaeWaaeaacaWG0baaca
GLOaGaayzkaaGaeyypa0ZaaSaaaeaacaWGtbWaaSbaaSqaaiaadkga
caWGHbGaamOCaaqabaGccaWGfbWaaSbaaSqaaiaadkgacaWGHbGaam
OCaaqabaaakeaacaaIYaGaam4uamaaBaaaleaacaWGZbGaamiCaiaa
dwgacaWGJbGaamyAaiaad2gacaWGLbGaamOBaaqabaaaaOWaamWaae
aacqaH1oqzdaWgaaWcbaGaamiBaaqabaGcdaqadaqaaiaadshaaiaa
wIcacaGLPaaacqGHRaWkcqaH1oqzdaWgaaWcbaGaamOuaaqabaGcda
qadaqaaiaadshaaiaawIcacaGLPaaacqGHRaWkcqaH1oqzdaWgaaWc
baGaamivaaqabaGcdaqadaqaaiaadshaaiaawIcacaGLPaaaaiaawU
facaGLDbaaaaa@6B8B@
ここで、
ε
I
ε
R
入力応力波に対するひずみ。
ε
T
出力応力波に対するひずみ。
試験体の真応力は次の関係式で計算することができます(詳細については
例題 11 - 引張試験 をご参照ください):
(4)
σ
t
r
u
e
=
σ
e
n
g
i
n
e
e
r
i
n
g
exp
(
ε
t
r
u
e
)
真ひずみは以下で与えられます:(5)
ε
˙
=
Δ
ε
t
r
u
e
Δ
t
真応力と真ひずみは破壊の点まで評価できます。
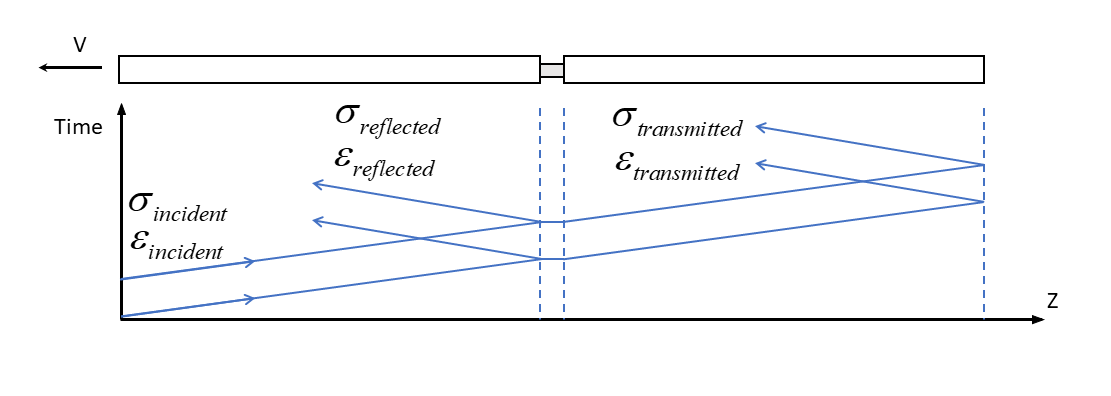
図 5. 1D解析
インターフェース1
F
1
=
S
b a r
[
σ
l
(
t
) +
σ
R
(
t
) ] =
S
b a r
⋅
E
b a r
[
ε
l
(
t
) +
ε
R
(
t
) ]
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbWaaS
baaSqaaiaaigdaaeqaaOGaeyypa0Jaam4uamaaBaaaleaacaWGIbGa
amyyaiaadkhaaeqaaOWaamWaaeaacqaHdpWCdaWgaaWcbaGaamiBaa
qabaGcdaqadaqaaiaadshaaiaawIcacaGLPaaacqGHRaWkcqaHdpWC
daWgaaWcbaGaamOuaaqabaGcdaqadaqaaiaadshaaiaawIcacaGLPa
aaaiaawUfacaGLDbaacqGH9aqpcaWGtbWaaSbaaSqaaiaadkgacaWG
HbGaamOCaaqabaGccqGHflY1caWGfbWaaSbaaSqaaiaadkgacaWGHb
GaamOCaaqabaGcdaWadaqaaiabew7aLnaaBaaaleaacaWGSbaabeaa
kmaabmaabaGaamiDaaGaayjkaiaawMcaaiabgUcaRiabew7aLnaaBa
aaleaacaWGsbaabeaakmaabmaabaGaamiDaaGaayjkaiaawMcaaaGa
ay5waiaaw2faaaaa@63CE@
インターフェース2
F
2
=
S
b a r
⋅
σ
T
(
t
) =
S
b a r
⋅
E
b a r
⋅
ε
T
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbWaaS
baaSqaaiaaikdaaeqaaOGaeyypa0Jaam4uamaaBaaaleaacaWGIbGa
amyyaiaadkhaaeqaaOGaeyyXICTaeq4Wdm3aaSbaaSqaaiaadsfaae
qaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0Jaam4uamaa
BaaaleaacaWGIbGaamyyaiaadkhaaeqaaOGaeyyXICTaamyramaaBa
aaleaacaWGIbGaamyyaiaadkhaaeqaaOGaeyyXICTaeqyTdu2aaSba
aSqaaiaadsfaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaaaaa@5803@
試験体のバランス
F
1
=
F
2
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGgbWaaS
baaSqaaiaaigdaaeqaaOGaeyypa0JaamOramaaBaaaleaacaaIYaaa
beaaaaa@3BDD@
ε
l
(
t
)
+
ε
R
(
t
)
=
ε
T
(
t
)
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH1oqzda
WgaaWcbaGaamiBaaqabaGcdaqadaqaaiaadshaaiaawIcacaGLPaaa
cqGHRaWkcqaH1oqzdaWgaaWcbaGaamOuaaqabaGcdaqadaqaaiaads
haaiaawIcacaGLPaaacqGH9aqpcqaH1oqzdaWgaaWcbaGaamivaaqa
baGcdaqadaqaaiaadshaaiaawIcacaGLPaaaaaa@490E@
試験体の公称応力
σ
s p e c i m e n
(
t
) =
F
1
S
s p e c i m e n
=
F
2
S
s p e c i m e n
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHdpWCda
WgaaWcbaGaam4CaiaadchacaWGLbGaam4yaiaadMgacaWGTbGaamyz
aiaad6gaaeqaaOWaaeWaaeaacaWG0baacaGLOaGaayzkaaGaeyypa0
ZaaSaaaeaacaWGgbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaam4uamaa
BaaaleaacaWGZbGaamiCaiaadwgacaWGJbGaamyAaiaad2gacaWGLb
GaamOBaaqabaaaaOGaeyypa0ZaaSaaaeaacaWGgbWaaSbaaSqaaiaa
ikdaaeqaaaGcbaGaam4uamaaBaaaleaacaWGZbGaamiCaiaadwgaca
WGJbGaamyAaiaad2gacaWGLbGaamOBaaqabaaaaaaa@5A0E@
ひずみ速度フィルタリング
動的荷重のために、ひずみ速度には物理的ではない高い周波数の振動が生じます。このため、応力-ひずみ曲線にはノイズが現れます。滑らかな結果を得るためにひずみ速度のフィルタリングオプションで高周波振動を除去してこのような振動を減衰させることができます。この例では、ひずみ速度のフィルタリングのためにカットオフ周波数F cut RD-E:1100 引張試験 をご参照ください。
Johnson-Cookモデル
Johnson-Cookモデルは、以下の式を用いて応力を塑性ひずみとひずみ速度の関係式で記述します:
(6)
σ
=
(
a
+
b
ε
p
n
)
︸
Influence of
plastic strain
(
1
+
c
ln
ε
˙
ε
˙
0
)
︸
Influence of
strain rate
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaHdpWCcq
GH9aqpdaagaaqaamaabmaabaGaamyyaiabgUcaRiaadkgacqaH1oqz
daWgaaWcbaGaamiCaaqabaGcdaahaaWcbeqaaiaad6gaaaaakiaawI
cacaGLPaaaaSabaeqabaqcfaOaaeysaiaab6gacaqGMbGaaeiBaiaa
bwhacaqGLbGaaeOBaiaabogacaqGLbGaaeiiaiaab+gacaqGMbGaae
iiaaWcbaqcfaOaaeiCaiaabYgacaqGHbGaae4CaiaabshacaqGPbGa
ae4yaiaabccacaqGZbGaaeiDaiaabkhacaqGHbGaaeyAaiaab6gaaa
GccaGL44padaagaaqaamaabmaabaGaaGymaiabgUcaRiaadogaciGG
SbGaaiOBamaalaaabaGafqyTduMbaiaaaeaacuaH1oqzgaGaamaaBa
aaleaacaaIWaaabeaaaaaakiaawIcacaGLPaaaaSabaeqabaqcfaOa
aeysaiaab6gacaqGMbGaaeiBaiaabwhacaqGLbGaaeOBaiaabogaca
qGLbGaaeiiaiaab+gacaqGMbGaaeiiaaWcbaqcfaOaae4Caiaabsha
caqGYbGaaeyyaiaabMgacaqGUbGaaeiiaiaabkhacaqGHbGaaeiDai
aabwgaaaGccaGL44paaaa@8086@
ここで、
ε
˙
ひずみ速度。
ε
˙
0
参照ひずみ速度
ε
p
塑性ひずみ(真ひずみ)。
a
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
降伏応力。
b
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
硬化パラメータ
n
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
硬化指数
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
ひずみ速度係数。
2つのオプション入力、ひずみ速度係数と参照ひずみ速度がそれぞれの材料の/MAT/LAW2 で応力のひずみ速度効果を考慮するために定義する必要があり、これでひずみ速度が増加したときに応力が増加します。定数
a
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
b
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
n
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGHbaaaa@384E@
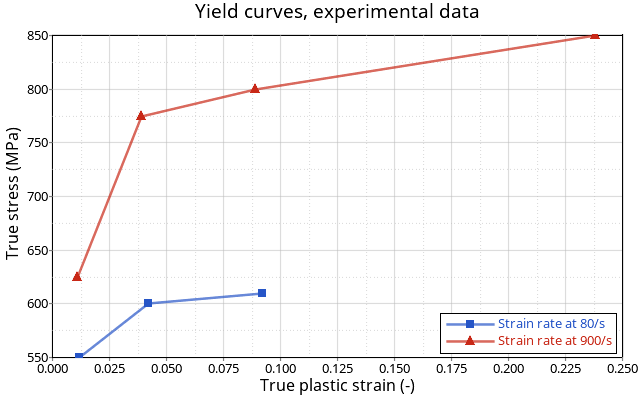
CRAHVI, G4RD-CT-2000-00395, D.1.1.1, Material Tests – Tensile properties of Aluminum Alloys 7010T7651 および
AU4G Over a Range of Strain Rates というタイトルの文書では、7010アルミニウム鋳物は以下の関係で記述できます:
σ
=
(
496
+
225
ε
0.35
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqaHdpWCcqGH9aqpdaqadaqaaiaaisdacaaI5aGaaGOnaiabgUca
RiaaikdacaaIYaGaaGynaiabew7aLnaaCaaaleqabaGaaGimaiaac6
cacaaIZaGaaGynaaaaaOGaayjkaiaawMcaaaaa@4749@
ひずみ速度80 s-1 未満
σ
=
(
496
+
225
ε
0.35
)
(
1
+
0.16
ln
(
ε
˙
0.08
)
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqaHdpWCcqGH9aqpdaqadaqaaiaaisdacaaI5aGaaGOnaiabgUca
RiaaikdacaaIYaGaaGynaiabew7aLnaaCaaaleqabaGaaGimaiaac6
cacaaIZaGaaGynaaaaaOGaayjkaiaawMcaamaabmaabaGaaGymaiab
gUcaRiaaicdacaGGUaGaaGymaiaaiAdaciGGSbGaaiOBamaabmaaba
WaaSaaaeaacuaH1oqzgaGaaaqaaiaaicdacaGGUaGaaGimaiaaiIda
aaaacaGLOaGaayzkaaaacaGLOaGaayzkaaaaaa@556B@
ひずみ速度80 s-1 から3000 s-1 まで
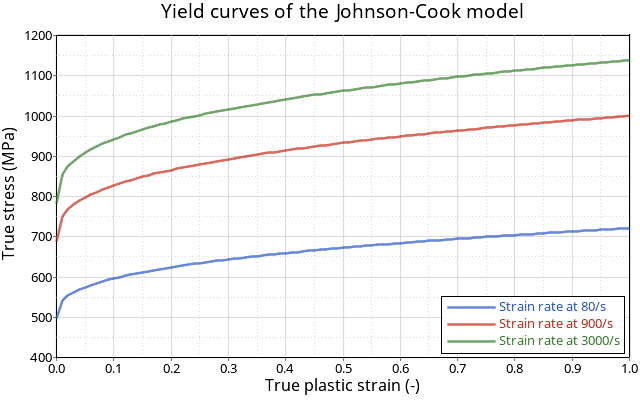
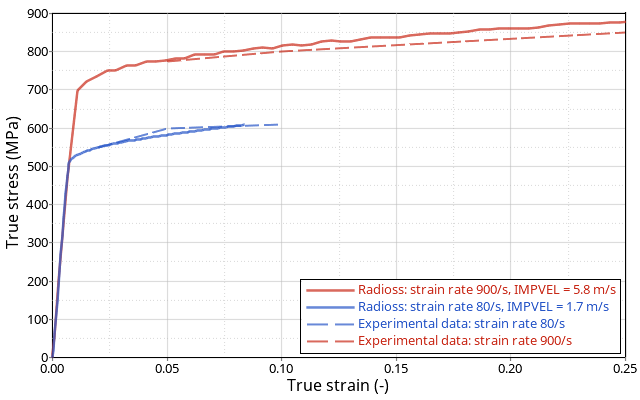
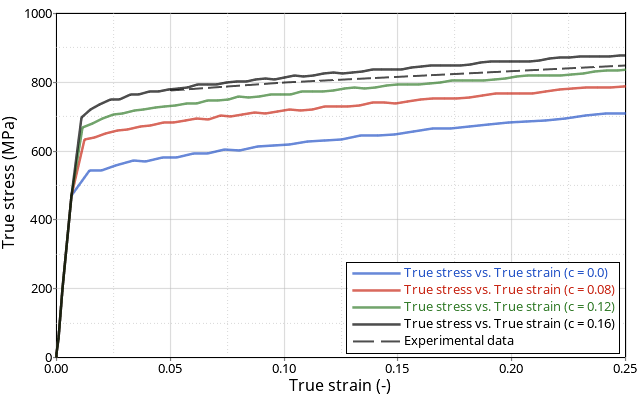
図 6. Johnson-Cookモデルの降伏曲線:
σ
=
(
496
+
225
ε
0.35
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqaHdpWCcqGH9aqpdaqadaqaaiaaisdacaaI5aGaaGOnaiabgUca
RiaaikdacaaIYaGaaGynaiabew7aLnaaCaaaleqabaGaaGimaiaac6
cacaaIZaGaaGynaaaaaOGaayjkaiaawMcaaaaa@4749@
試験体の材料特性は:
材料特性 ヤング率
73000
[
MPa
]
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai
Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
ポアソン比
0.33
密度
0.0028
[
g
m
m
3
]
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada
WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
バード飛翔体に用いられる材料はTYPE1(線形弾性)で以下の特性を持ちます:
材料特性 ヤング率
210000
[
MPa
]
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai
Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
ポアソン比
0.33
密度
0.0078
[
g
m
m
3
]
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada
WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
バーと飛翔体の幾何学的特性は:
バー 長さ
4 m
直径
12 mm
飛翔体 半径
12 mm
重量
170g
モデリング手法
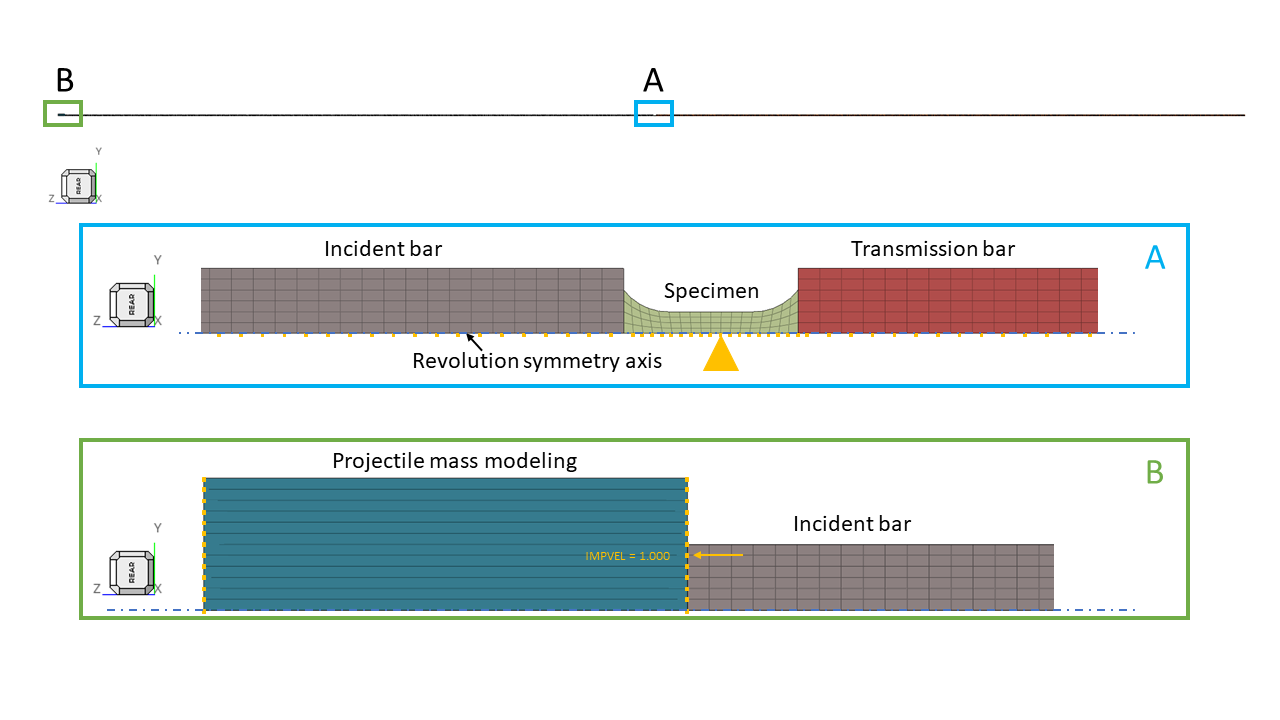
形状の回転対称を考慮し、材料と運動条件で、軸対称モデルが用いられます(Starterファイルの/ANALY オプションでN2D3D = 1 を設定)。Yが半径方向で、Zが回転軸となります。
メッシュは12054の2Dソリッド要素(QUAD)からなります。2Dソリッドの寸法は約2mmです。
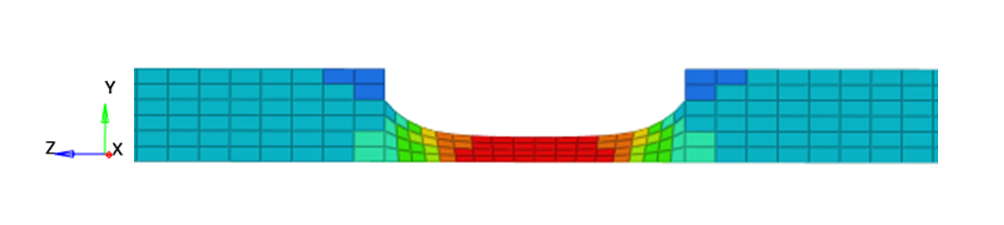
図 7. 入力バーの上部に強制速度の. 軸対称モデルのメッシュ