RD-E:0700 振り子
この例題の目的は、初期に相互に接触し、複数の衝撃を受ける複数の物体を通るエネルギー伝播と運動量伝達を検討することです。衝撃における衝突のプロセスとエネルギー挙動が3次元モデルを用いて表現されます。
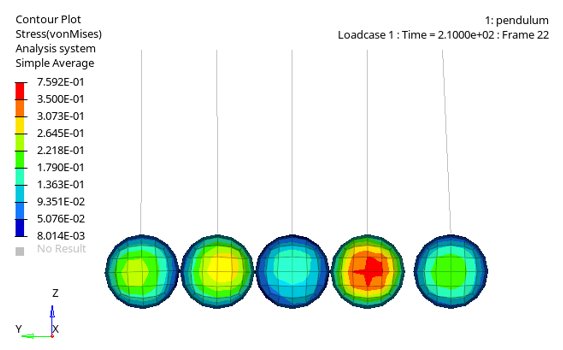
図 1.
この例題では、一列に配置された一連の振り子の一端に衝撃を受けた時の振動と波動伝播をシミュレートします。材料は弾性です。モデルの質は最初にどのように接触が取り扱われるかに依存します。このモデルには、ペナルティ法を用いたTYPE24接触インターフェースが使用されます。
使用されるオプションとキーワード
- 3次元解析、トラス(スレッド)、ソリッド要素とソリッド要素(六面体要素)
- /INTER/TYPE2
- /INTER/TYPE14
- ペナルティ法を使用した一般的な節点対サーフェスの接触インターフェース(/INTER/TYPE24)
- 弾性、運動量伝達、衝撃波の伝播、複数の衝撃。
- 重力(/GRAV)
- 並進および回転移動に対する節点グループ上の境界条件(/BCS)
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
本例題で使用されるモデルファイルは下記のとおり:
pendulum_*.rad
モデル概要
線上に並べられた4つの振り子が初期に相互に接触し、5番目の振り子により衝撃を受けます。衝撃波と振動の移動が観察されます。
単位: g、ms、mm、MPa
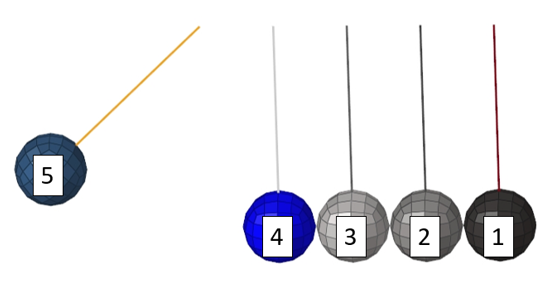
図 2. 初期状態の3次元メッシュ
- プロパティ
- ヤング率
- 70000
- ポアソン比
- 0.33
- 密度
- 0.0027
- トラス
- 長さ
- 124.6 mm
- ボール
- 半径
- 25.4 mm
- 質量
- 169.7g
TYPE24接触インターフェースでは、線形接触剛性によるペナルティ法を使用して、ボールどうしの接触をモデル化します。すべてのボールどうしの自己接触定義を使用して、節点と要素表面との接触をモデル化します。ペナルティ法を用いたインターフェースは、メイン / セカンダリ処理に基づいています。
ボールのモデル化にはソリッド要素を使用します。TYPE24インターフェースでは接触ギャップが不要です。
重力が全ての節点に与えられます。Z方向の重力加速度の定義には、時間に対する重力の関数が適用されます。重力は/GRAVオプションでアクティブになります。
トラスの上端では、X、Y、Z各方向の並進およびYとZの各軸を中心とした回転が拘束されています(X軸を中心とした回転は自由です)。
結果
このモデルの運動エネルギーの変化を考慮すると、この系は単純な1つの振り子としての挙動を示します(図 3)。
- ボール中心の鉛直変位
- 速度
- 質量
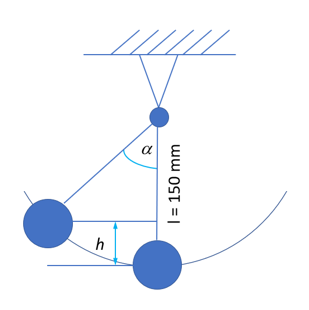
図 3. 振り子の移動
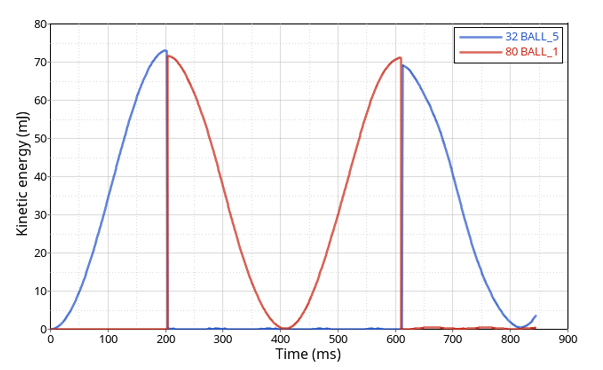
図 4. ボール5とボール1の間での運動エネルギー伝達
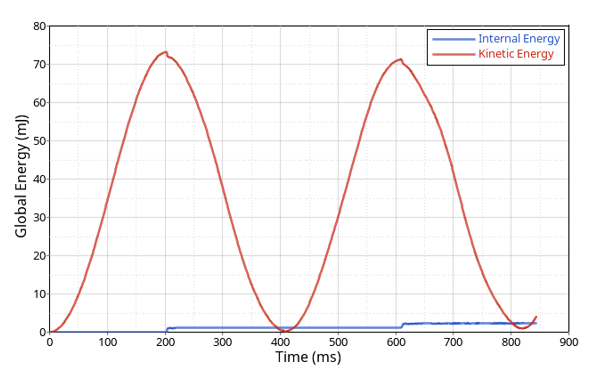
図 5. グローバルな内部エネルギーと運動エネルギー
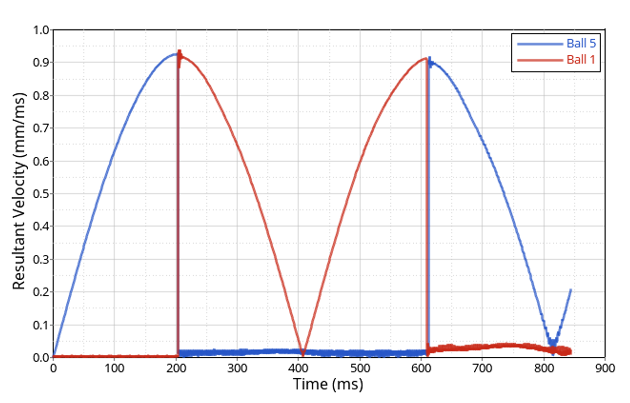
図 6. ボール5とボール1の速度曲線
まとめ
Radiossを使用して、一列に並んだ振り子のグループの振動と波動伝播を検討しました。このモデルでは、3D要素の粗いメッシュを使用して演算時間を短縮しています。接触は、ペナルティ法を使用した/INTER/TYPE24でモデル化しました。その結果を、この振り子の系を単純な1つの振り子と解釈して得られた解析解と比較しました。シミュレーションにより得られた結果と理論が、Radiossによって得られた数値結果の妥当性を示します。