RD-E:1900 波動伝播
鉛直に分布する荷重を受ける半空間上の弾性波の伝播
- Lagrange定式化
- ALE(Arbitrary Lagrangian Eulerian)定式化

図 1.
領域は弾性材料則プロセスの下で鉛直インパルス荷重を受けます。生成される衝撃波は縦波とせん断で構成されます。縦波が領域の下の境界に到達する予測として、結果は0.77 msを示しています。正確な波動の拡大を保証するため、ALE定式化ではサイレント境界(NRF)を用いた無限領域がモデル化されます。
使用されるオプションとキーワード
- 2次元解析(/ANALY)、2次元ソリッド、一般ソリッド
2次元問題が考慮されます。/ANALYで定義されるフラグN2D3Dが2にセットされます。2次元解析はX軸を平面ひずみの方向として定義します。
- インパルス荷重、波動伝播、縦波とせん断波
- ALEとLagrangeモデル化
- サイレント境界(NRF)材料、無限領域
- ALE定式化(/ALE/MAT)
- 集中荷重(/CLOAD)与えられる鉛直荷重は集中荷重(/CLOAD)で、サイン関数の形式で振幅 GPa、周期です。
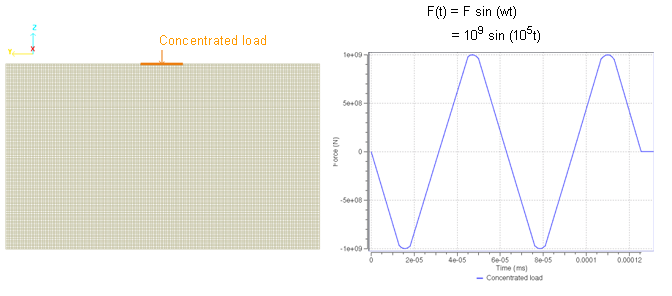
図 2. インパルス荷重の時間変化 - 関数(/FUNCT)
- サイレント境界(NRF)材料LAW11(/MAT/LAW11(BOUND))
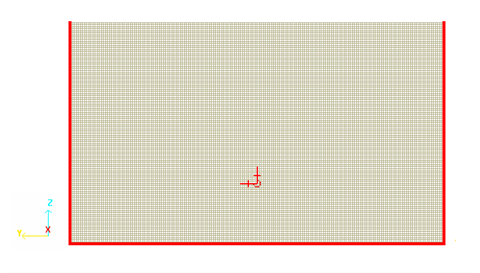
図 3. 固定された辺
このアプローチの制限は領域境界での反射です。シミュレーション結果は衝撃波が下側に達する前の時点で示されます(< 0.77 ms)。
- 材料特性
- 初期密度
- 2842 kg.m3
- 特性長さ
- 0.0632 m
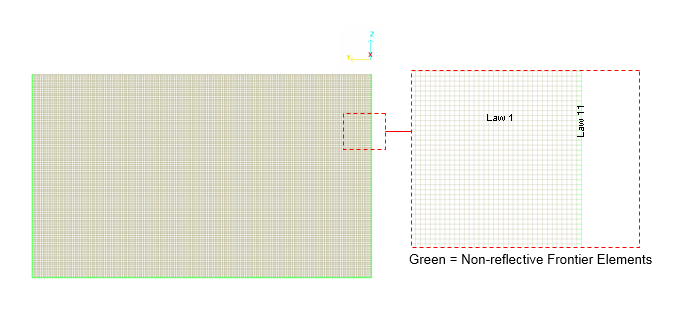
図 4. サイレント境界(NRF)材料LAW11(TYPE3)によりモデル化された無限領域
材料は入力ファイルで /ALE/MATオプションを用いてALEと宣言される必要があります。
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
単位: m、s、Kg、N、Pa
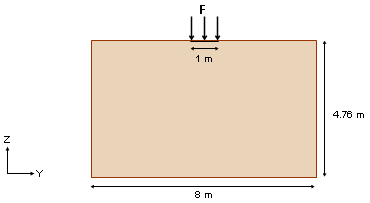
図 5. 問題のデータ
- 材料特性
- 初期密度
- 2842 kg.m-3
- ヤング率
- 73 GPa
- ポアソン比
- 0.33
衝撃化の拡大プロセスは縦波とせん断波からなります。
これらの材料の特性に基づき、材料内の縦波の伝播速度は6169.1 m.s-1でせん断波は3107.5 m.s-1です。したがって、縦波は領域の下の境界に約0.77 msで到達するはずです。
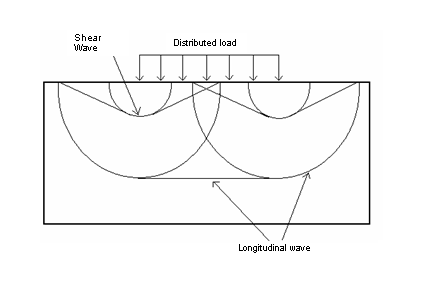
図 6. 波のパターンを構成する縦波とせん断波
インパルス荷重は次のサイン関数で記述されます:
モデリング手法
このパートは規則的なメッシュを用いて19080個のQUAD要素でモデル化されます(44.9 mm x 44.4 mm ここで =63.15 mm)。

図 7. 2次元領域のメッシュ
結果
LagrangeとALE結果の解析解との比較
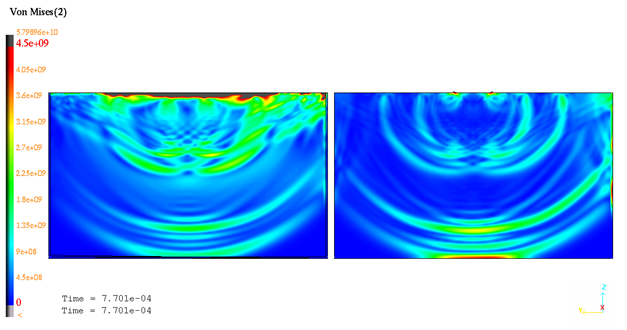
図 8. t=0.77 msにおけるvon Mises等値図
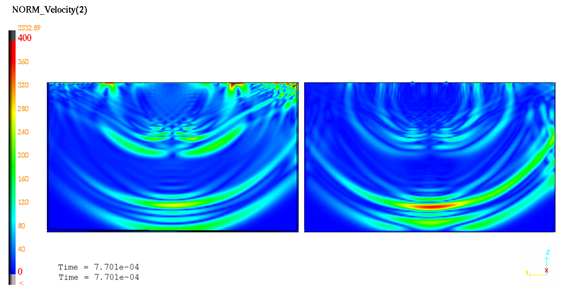
図 9. t=0.77 msにおける速度等値図
衝撃波伝播が、良好に予測されています。t=0.77msで得られたシミュレーション結果は解析解を裏付けます: 縦波とせん断波。
Lagrange結果
波のパターン
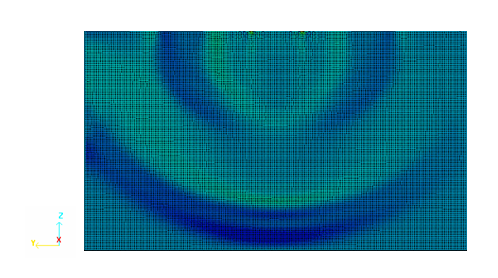
図 10. t=0.77 msにおける領域の波のパターン
鉛直変位
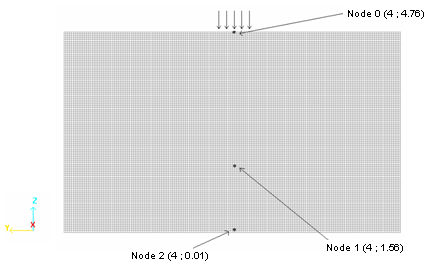
図 11. 時刻歴に保存された断面
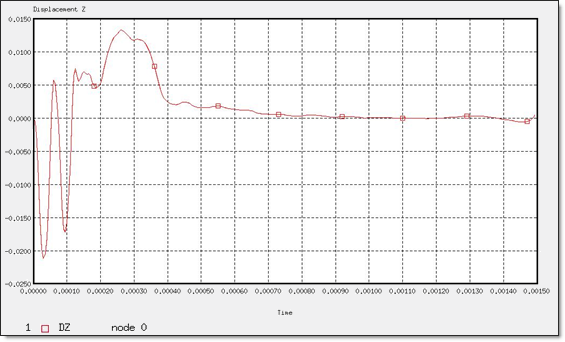
図 12. “節点 0”のZ方向変位
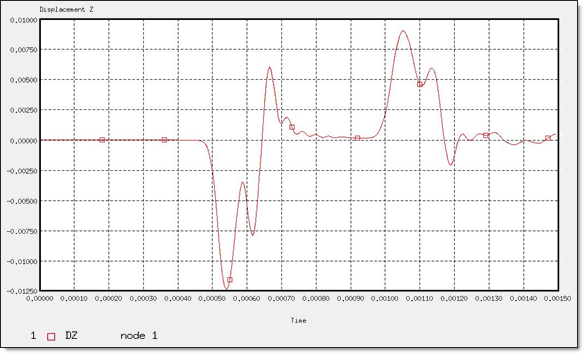
図 13. “節点 1”のZ方向変位
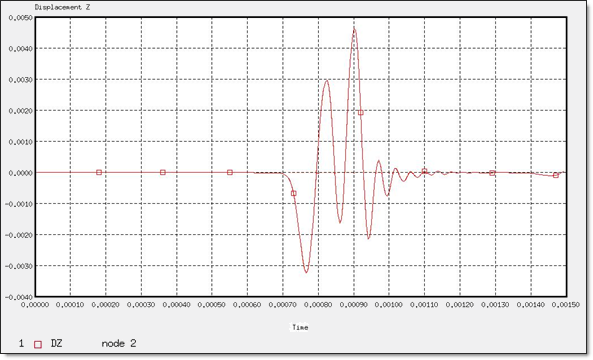
図 14. “節点 2”のZ方向変位
水平変位
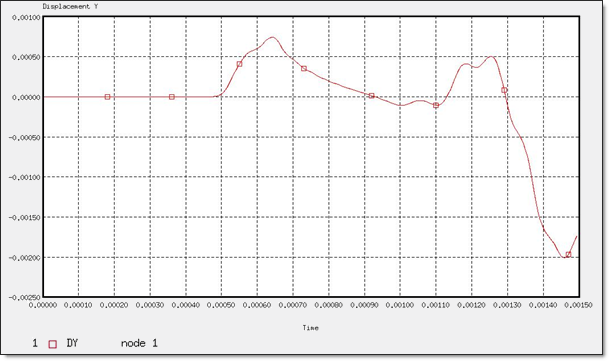
図 15. “節点 0”のY方向変位
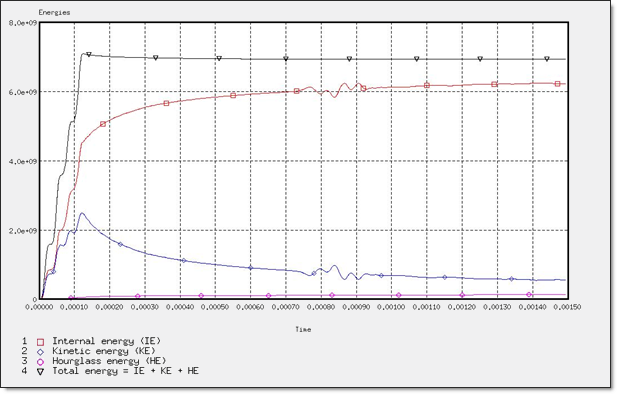
図 16. 全体エネルギー評価
ALE結果
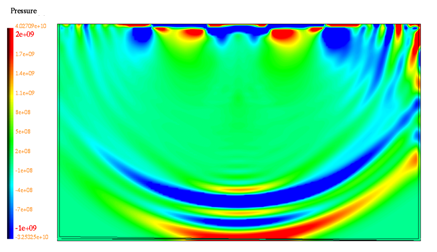
図 17. t=0.77 msにおける圧力等値図
まとめ
有限領域での波動伝播がLagrangeとALEアプローチを用いて検討されています。Lagrange定式化では、無限領域を定義することができません。縦波とせん断波の境界に対する反射がシミュレーションを時間に関して制限します(t < 0.77 ms)。ALEアプローチではサイレント境界(NRF)材料(LAW11 - LAW3)をその制限上に定義することにより、無限領域をモデル化することができます。このような特別なモデル化で拡大する波動の反射を最小化します。
2次元解析は平面的な伝播を示します。波のパターンの正確な表現が得られ、シミュレーション結果は解析解と近いものになっています。