RD-E：1803 弾塑性の正方形の膜

この例題は、2つの集中荷重を受ける埋め込まれた板のねじりの問題に関するものです。この例題ではメッシュにおける異なる要素定式化の役割を示します。

使用されるオプションとキーワード

  • Q4シェル
  • T3シェル
  • アワグラスおよびメッシュ
  • 境界条件（/BCS）

    境界条件では1つの側の3つの節点と、2つの中間節点が拘束され、他はY軸に関して自由です。

  • 集中荷重（/CLOAD）
    2つの集中荷重が反対側の角の点に作用されます。これは、次の関数で定義されたように時間で増加します：
    F(t) 0 10 10
    t 0 200 400

    rad_ex_fig_18-19
    図 1. 境界条件と拘束

入力ファイル

必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。

モデル概要

単位： mm、ms、g、N、 MPa

用いた材料は等方性弾塑性挙動に従い、Johnson-Cook塑性モデル（/MAT/LAW2）で、以下の特性値を持ちます：
材料特性
初期密度
7.8x10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
ヤング率
210000 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
ポアソン比
0.3
降伏応力
206 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
硬化パラメータ
450 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
硬化指数
0.5
最大応力
340 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@

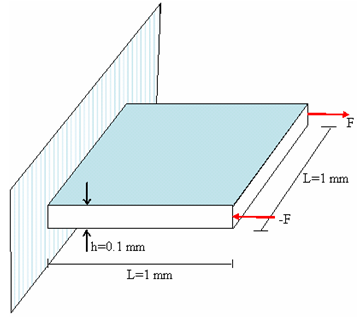
rad_ex_fig_18-17
図 2. 問題の形状

モデリング手法

4つのシェルが異なるタイプのメッシュでモデル化されます：
メッシュ 1
2つの四角形シェルと4つの三角形シェル （2Q4-4T3）
メッシュ 2
4つの四角形シェル（4Q4）
メッシュ 3
8つの三角形シェル（8T3）
メッシュ 4
8つの三角形シェル（8T3逆向き）
それぞれのモデルで、以下のシェル定式化がテストされます：
  • QBAT定式化（Ishell =12）
  • QEPH定式化（Ishell =24）
  • Belytshcko&Tsay定式化（Ishell=1または3、アワグラスコントロールタイプTYPE1、TYPE3）
  • C0とDKT18定式化

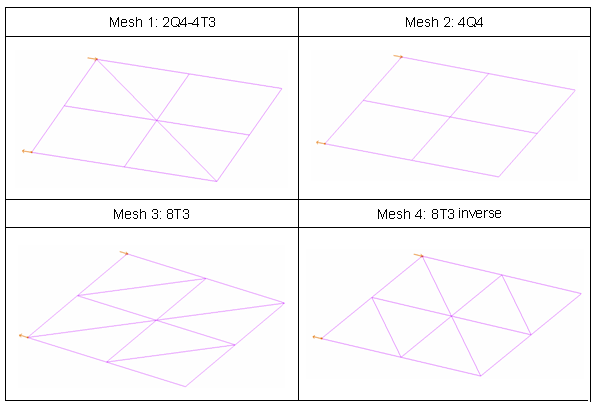
rad_ex_fig_18-18
図 3. 正方形板メッシュ

結果

曲線とアニメーション

この例では、いくつかのモデルを比較します：
  • それぞれのメッシュに対する異なるシェル要素定式化の使用
  • 与えられてシェル定式化に対する異なるタイプのメッシュ
結果を比較するために、2つの基準が用いられます：
  • 吸収エネルギー（内部とアワグラス）
  • 荷重を受けた点の鉛直変位

以下の図に得られた結果をまとめます。

エネルギー曲線 / 要素定式化の比較

メッシュ 1：2Q4-4T3

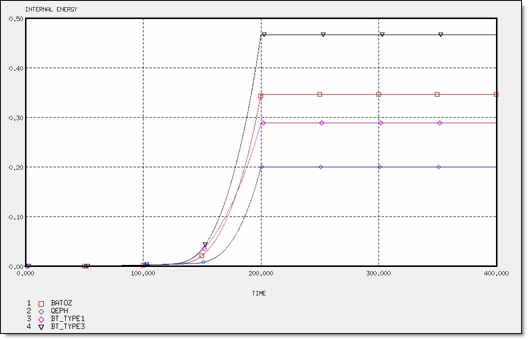
rad_ex_fig_18-20
図 4. 2 x Q4と4 x T3要素の内部エネルギー

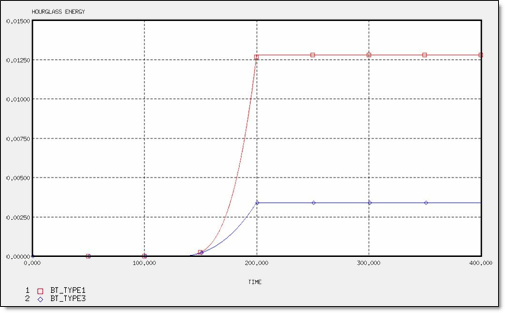
rad_ex_fig_18-21
図 5. 2 x Q4と4 x T3要素のアワグラスエネルギー

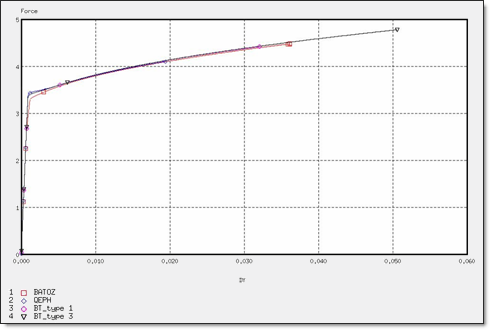
rad_ex_fig_18-22
図 6. 4 x Q4要素の力
メッシュ 2：4Q4

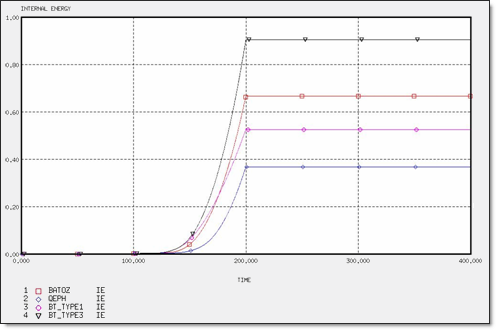
rad_ex_fig_18-23
図 7. 4 x Q4要素の内部エネルギー

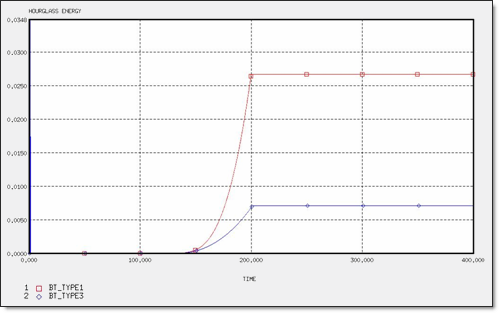
rad_ex_fig_18-24
図 8. 4 x Q4要素のアワグラスエネルギー

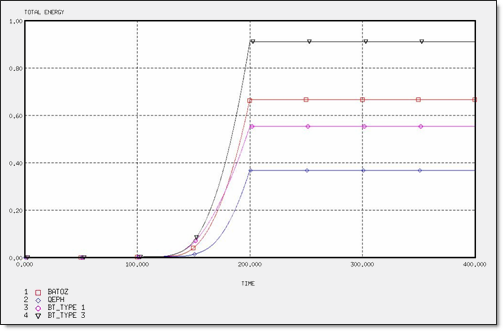
rad_ex_fig_18-25
図 9. 4 x Q4要素の全エネルギー

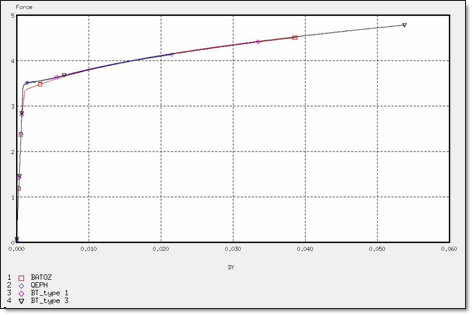
rad_ex_fig_18-26
図 10. 4 x Q4要素の力

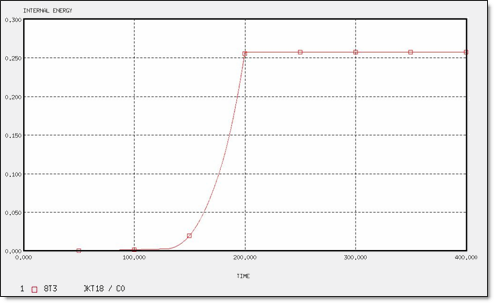
rad_ex_fig_18-27
図 11. 8 x T3要素の内部エネルギー

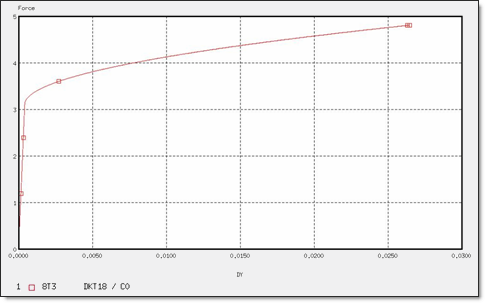
rad_ex_fig_18-28
図 12. 8 x T3要素の力
メッシュ 4：8T3_INV

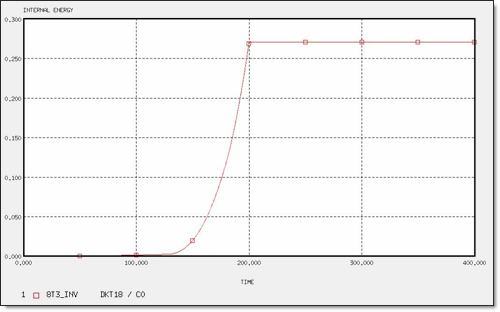
rad_ex_fig_18-29
図 13. 8 x T3要素の内部エネルギー（逆向きメッシュ）

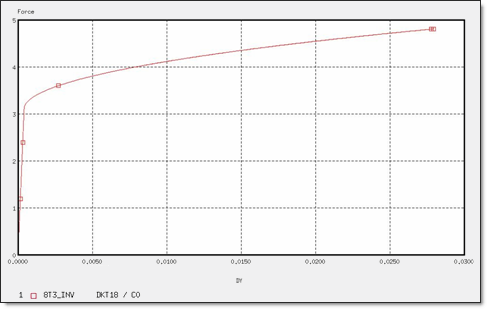
rad_ex_fig_18-30
図 14. 8 x T3要素の力（逆向きメッシュ）

異なるメッシュの比較


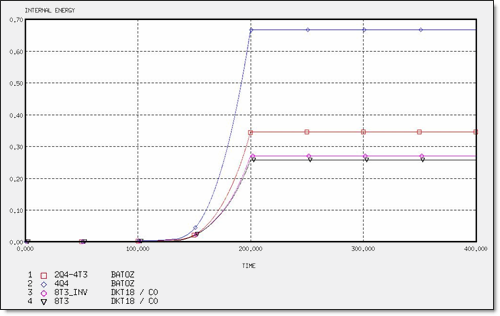
rad_ex_fig_18-31
図 15. 異なるメッシュでの内部エネルギー

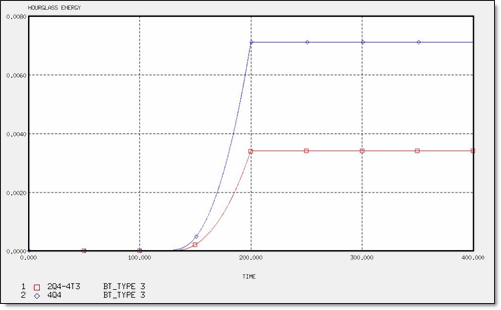
rad_ex_fig_18-32
図 16. 異なるメッシュでのアワグラスエネルギー

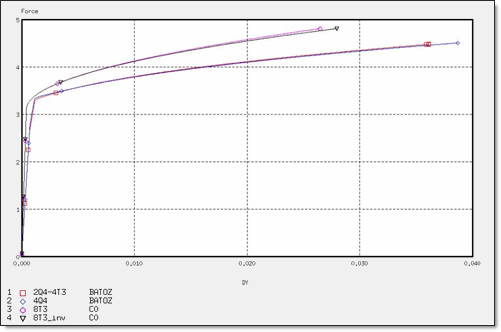
rad_ex_fig_18-33
図 17. 異なるメッシュでの力
表 1. 変位と最大エネルギー比較
プラスチック 2Q4-4T3 4Q4 8T3： 8T3_INV
QEPH BT_TYPE 1 BT_TYPE 3 BATOZ QEPH BT_TYPE 1 BT_TYPE 3 BATOZ DKT CO DKT CO
IEmax 2.37 x 10-1 2.89 x 10-1 3.03 x 10-1 3.46 x 10-1 2.69 x 10-1 5.27 x 10-1 5.67 x 10-1 6.67 x 10-1 2.57 x 10-1 2.57 x 10-1 2.70 x 10-1 2.70 x 10-1
HEmax -- 1.26 x 10-2 2.13 x 10-2 -- -- 2.66 x 10-2 4.41 x 10-2 -- -- -- -- --
全エネルギー 2.37 x 10-1 3.02 x 10-1 3.24 x 10-1 3.46 x 10-1 2.96 x 10-1 5.54 x 10-1 6.11 x 10-1 6.67 x 10-1 2.57 x 10-1 2.57 x 10-1 2.70 x 10-1 2.70 x 10-1
Dymax 2.36 x 10-2 3.20 x 10-2 3.35 x 10-2 3.61 x 10-2 1.72 x 10-2 3.34 x 10-2 3.56 x 10-2 3.87 x 10-2 2.64 x 10-2 2.64 x 10-2 2.79 x 10-2 2.79 x 10-2
ε p max 2.76 x 10-2 3.78 x 10-2 3.97 x 10-2 4.43 x 10-2 1.87 x 10-2 3.72 x 10-2 3.97 x 10-2 4.50 x 10-2 6.28 x 10-2 6.28 x 10-2 6.28 x 10-2 6.28 x 10-2

まとめ

この例題の目的は、Radiossシェルの定式化時の弾塑性の取り扱いの役割を把握することにありました。面内の塑性がここでは考慮されます。この板の作用される境界条件とポアソン効果のため、テストは低減積分要素の塑性挙動に対して非常にシビアであるかも知れません。

4つの四角形メッシュのケースでは、QBAT要素が要素上の4積分点が可能なために、常に最良の結果を与えています。これにより、積分点での塑性計算が正確です。低減積分要素では、中央に1積分点だけのため、メッシュの幅を通して2積分点のみが置かれることになります。もう1つの点は、塑性計算でのポアソン比の役割に関するものです。実際QEPH要素は、ポアソン比に関する正確な考慮によりアワグラスエネルギーの解析的表現を用います（詳細については、Radioss Theory Manualをご参照ください）。しかしながら、弾塑性定式化ではいくつかの近似が含まれ、特に加工硬化が低いレベルの時に結果に影響する可能性があります。TYPE3アワグラスコントロールでのBT要素定式化は、その塑性部分へのアワグラス変形のポアソン比の効果はその役割を最小化する単純化された表現で計算されます。実際、BT_TYPE3で得られた結果は υ の変化に微妙に影響されます（検討された例題で υ =0を用いて得られた結果を比較してみてください）。BT要素は一般的によりフレキシブルで、非常に粗いメッシュでより良い結果を与えます。

三角形メッシュでは、DKT18の面内挙動がT3C0要素と同じであることに注意を払う必要があります。実際、要素はその曲げ挙動に関しては本質的に異なります。

T3とQ4要素を組み合わせた時、結果は一般的に均一な三角形メッシュと四角形メッシュの間のレベルとなります。