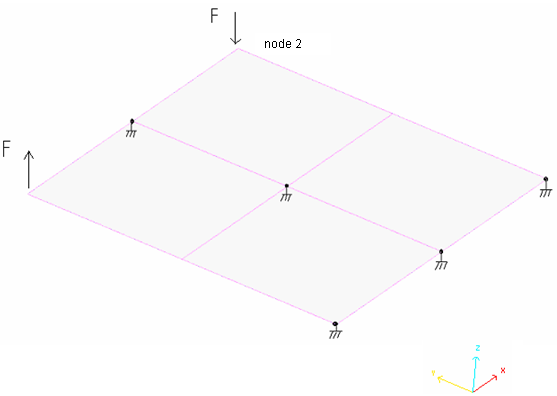
RD-E：1801 正方形板のねじり
この例題は、2つの集中荷重を受ける埋め込まれた板のねじりの問題に関するものです。この例題ではメッシュにおける異なる要素定式化の役割を示します。
使用されるオプションとキーワード
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
単位： mm、ms、g、N、 MPa
用いられた材料は線形弾性挙動に従い、以下の特性を持ちます:
- 材料特性
- 初期密度
- 7.8x10-3
- ヤング率
- 210000
- ポアソン比
- 0.3
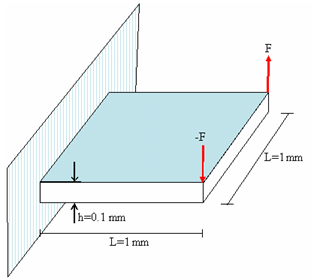
図 2. 問題の形状
モデリング手法
4つの異なるタイプのメッシュが用いられます：
- メッシュ 1
- 2つの四角形シェルと4つの三角形シェル （2Q4-4T3）
- メッシュ 2
- 4つの四角形シェル（4Q4）
- メッシュ 3
- 8つの三角形シェル（8T3）
- メッシュ 4
- 8つの三角形シェル（8T3逆向き）
それぞれのモデルで、以下のシェル定式化がテストされます：
図 3. 正方形板メッシュ
- QBAT定式化（Ishell =12）
- QEPH定式化（Ishell =24）
- Belytshcko&Tsay定式化（Ishell=1または3、アワグラスコントロールタイプTYPE1、TYPE3）
- C0とDKT18定式化
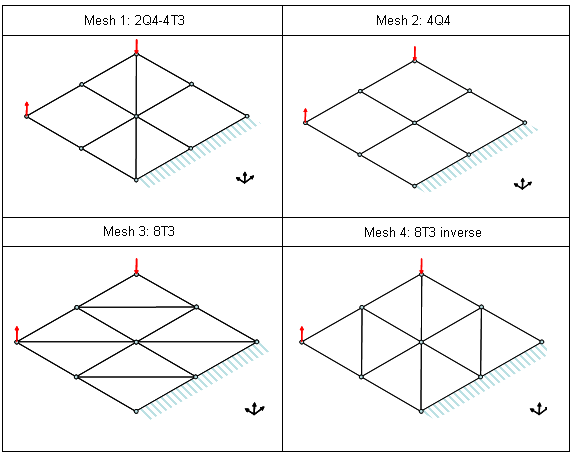
図 3. 正方形板メッシュ
結果
曲線とアニメーション
この例では、いくつかのモデルを比較します：
- それぞれのメッシュに対する異なるシェル要素定式化の使用
- 与えられてシェル定式化に対する異なるタイプのメッシュ
結果を比較するために、2つの基準が用いられます：
- 吸収エネルギー（内部とアワグラス）
- 荷重を受けた点の鉛直変位
以下の図に得られた結果をまとめます。
エネルギー曲線 / 要素定式化の比較
メッシュ 1： 2Q4-4T3
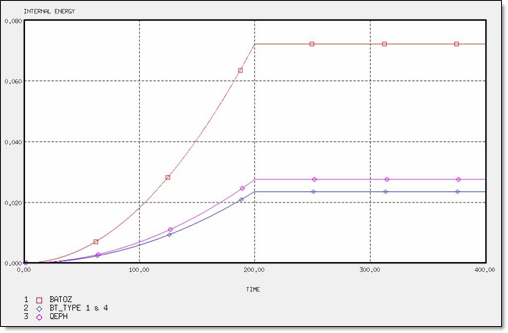
図 4. 2 x Q4と4 x T3要素の内部エネルギー
メッシュ 2：4Q4
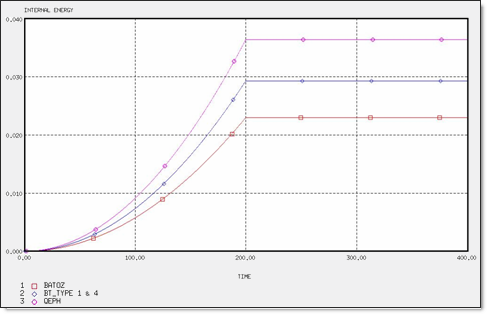
図 5. 4 x Q4要素の内部エネルギー
メッシュ 3と4： 8T3 と 8T3_INV
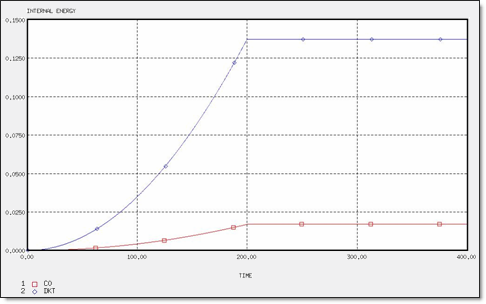
図 6. 8 x T3要素の内部エネルギー
エネルギー曲線 / メッシュ定義の比較
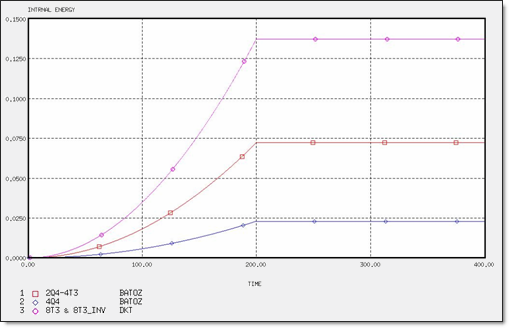
図 7. 異なるメッシュでの内部エネルギー
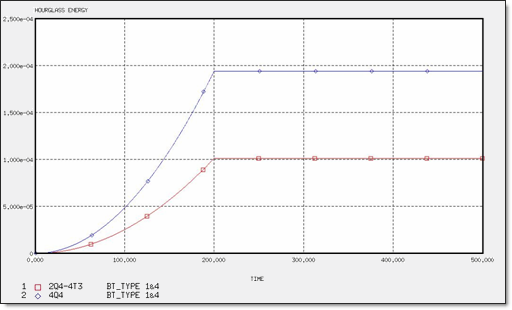
図 8. 異なるメッシュでのアワグラスエネルギー
| 2 Q4- 4 T3 | 4 Q4 | 8 T3 | 8 T3逆向き | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QEPH | BT_TYPE1 | BT_TYPE4 | BATOZ | QEPH | BT_TYPE1 | BT_TYPE4 | BATOZ | DKT | C0 | DKT | C0 | |
| IEmax | 2.74x10-2 | 2.35x10-2 | 2.37x10-2 | 7.21x10-2 | 3.64x10-2 | 2.93x10-2 | 2.97x10-2 | 2.30x10-2 | 1.37 x10-1 | 1.69x10-2 | 1.37x10-1 | 1.69x10-2 |
| HEmax | -- | 1.01x10-4 | 1.03x10-4 | -- | -- | 1.94x10-4 | 1.98x10-6 | -- | -- | -- | -- | -- |
| DZmax | 1.75x10-3 | 1.78x10-3 | 1.78x10-3 | 1.21x10-2 | 2.42x10-3 | 2.95x10-3 | 2.97x10-3 | 2.30x10-3 | 1.44x10-2 | 1.69x10-3 | 1.44x10-2 | 1.69x10-3 |
まとめ
ねじりを受ける正方形板はシェル要素のねじり-曲げを検討するための厳しいテストです。得られた結果概要から以下のポイントについて確認できます：
- 4Q4メッシュでは、QBATOZとQEPHを用いて得られた結果は良く似ています。BT要素は柔らかすぎますが、平面のメッシュのためアワグラス定式化にはそれほど大きく影響されません。
- 三角形メッシュではDKT要素は非常によく曲がりますが、C0要素は硬すぎます。
- Q4とT3要素の両方を用いたメッシュでは、1つのパートがRadiossの三角形要素も用いているため、上の2つのコメントと同じことは言えないかもしれません。