RD-E：1802 弾性の正方形の膜
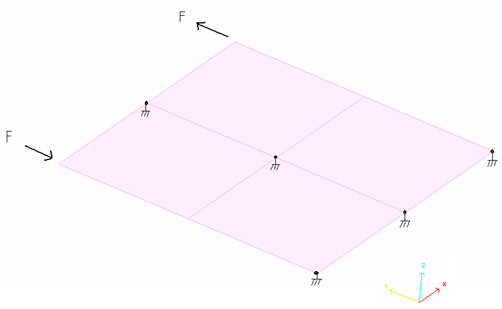
この例題は図 2に示すように2つの集中荷重を受ける埋め込まれた板の平面内の引張比較の問題に関するものです。
この例題ではメッシュにおける異なる要素定式化の役割を示します。
使用されるオプションとキーワード
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
単位： mm、ms、g、N、 MPa
用いられた材料は線形弾性挙動に従い、以下の特性を持ちます:
図 2. 問題の形状
- 材料特性
- 初期密度
- 7.8x10-3
- ヤング率
- 210000
- ポアソン比
- 0.3
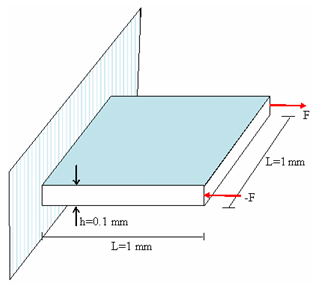
図 2. 問題の形状
モデリング手法
4つの異なるタイプのメッシュが用いられます：
- メッシュ 1
- 2つの四角形シェルと4つの三角形シェル （2Q4-4T3）
- メッシュ 2
- 4つの四角形シェル（4Q4）
- メッシュ 3
- 8つの三角形シェル（8T3）
- メッシュ 4
- 8つの三角形シェル（8T3逆向き）
それぞれのモデルで、以下のシェル定式化がテストされます：
図 3. 正方形板メッシュ
- QBAT定式化（Ishell =12）
- QEPH定式化（Ishell =24）
- Belytshcko&Tsay定式化（Ishell=1または3、アワグラスコントロールタイプTYPE1、TYPE3）
- C0とDKT18定式化
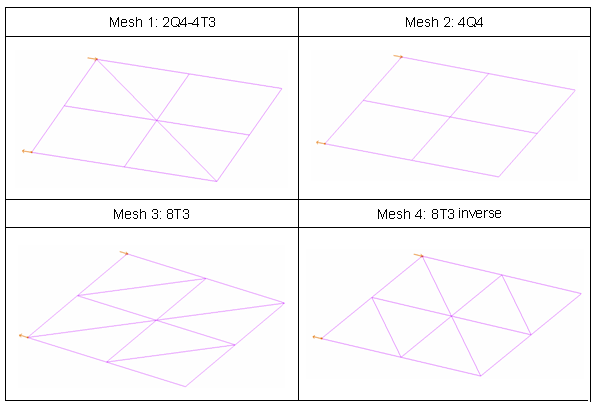
図 3. 正方形板メッシュ
結果
曲線とアニメーション
この例では、いくつかのモデルを比較します：
- それぞれのメッシュに対する異なるシェル要素定式化の使用
- 与えられてシェル定式化に対する異なるタイプのメッシュ
結果を比較するために、2つの基準が用いられます：
- 吸収エネルギー（内部とアワグラス）
- 荷重を受けた点の鉛直変位
以下の図に得られた結果をまとめます。
エネルギー曲線 / 要素定式化の比較
メッシュ 1：2Q4-4T3
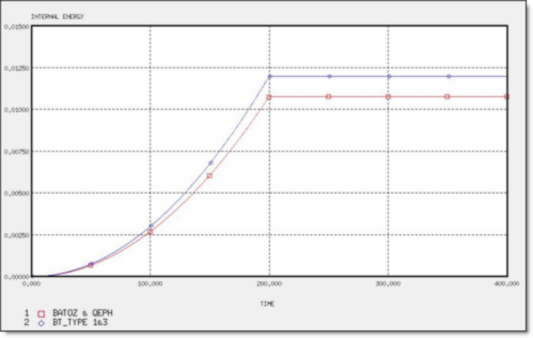
図 4. 2 x Q4と4 x T3要素の内部エネルギー
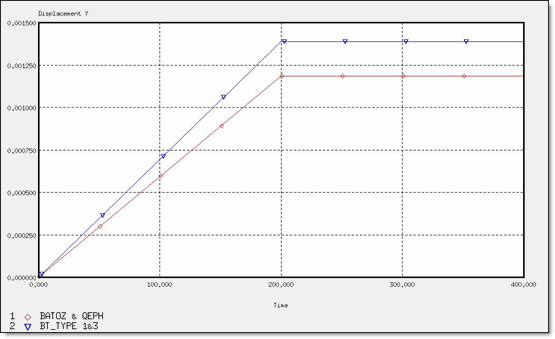
図 5. 2 x Q4と4 x T3要素のY方向変位
メッシュ 2：4Q4
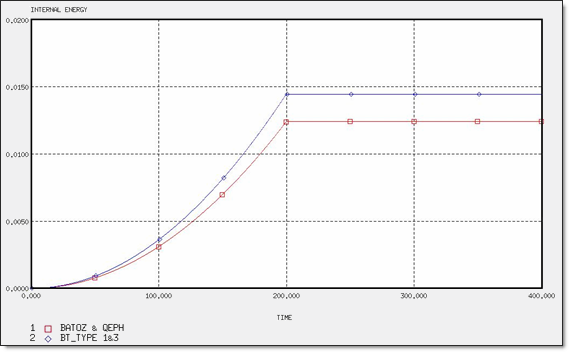
図 6. 4 x Q4要素の内部エネルギー
エネルギー曲線 / メッシュ定義の比較
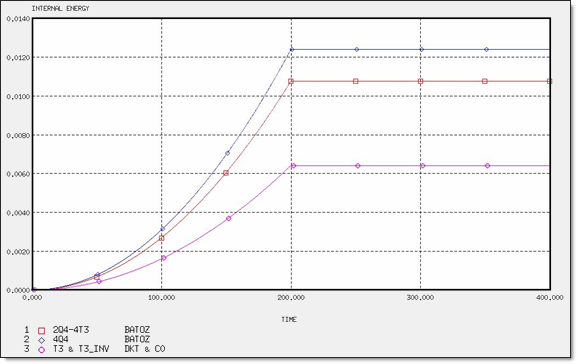
図 7. 異なるメッシュでの内部エネルギー
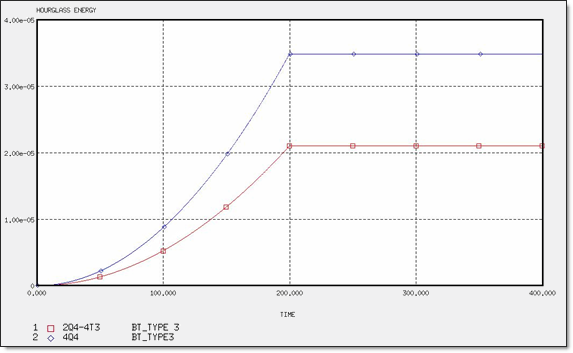
図 8. 異なるメッシュでのアワグラスエネルギー
| 弾性板 | 2Q4-4T3 | 4Q4 | 8T3： | 8T3_INV | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| QEPH | BT_TYPE 1 と 3 | BATOZ | QEPH | BT_TYPE 1 と 3 | BATOZ | DKT | CO | DKT | CO | |
| IEmax | 1.07 x 10-2 | 1.19 x 10-2 | 1.07 x 10-2 | 1.24 x 10-2 | 1.44 x 10-2 | 1.24 x 10-2 | 6.42 x 10-3 | 6.42 x 10-3 | 6.42 x 10-3 | 6.42 x 10-3 |
| HEmax | --- | 2.10 x 10-5 | -- | -- | 3.49 x 10-6 | -- | -- | -- | -- | -- |
| Dymax | 1.18 x 10-3 (引張) | 1.38 x 10-3 (引張) | 1.18 x 10-3 (引張) | 1.24 x 10-3 | 1.44 x 10-3 | 1.24 x 10-3 | 6.42 x 10-3 | 6.42 x 10-3 | 6.42 x 10-3 | 6.42 x 10-3 |
まとめ
弾性の平板のモデル化のケースでは、荷重が平面内の時、荷重が座屈を引き起こさない場合には、シェル要素は膜に帰着します。
得られた結果概要から以下のポイントについて確認できます：
- 矩形シェル要素QEPHおよびQBATは、同じ面内挙動を持ちます。
- BTでの異なるタイプのアワグラス定式化は、面外変形がなく、材料が弾性と想定される場合には同じ結果を生みます。
- DKT18とT3C0のRadioss三角形の3つの面内挙動は、両方の要素が面内に関しては同じ定式化を用いるため厳密に同じになります。
- 三角形は矩形要素よりも堅く、特にメッシュが粗い場合には良い結果は与えません。
詳細については、Radioss Theory Manualをご参照ください。