RD-E:2400 薄板加工
2つの転がる剛な円柱が板を押し潰して薄板化します。
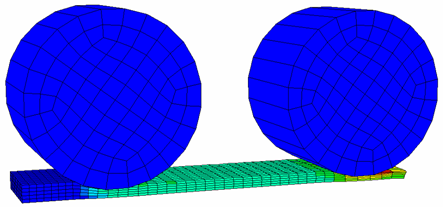
図 1.
使用されるオプションとキーワード
- ソリッド要素、ソリッド定式化、共回転定式化、完全積分要素
- 一定圧力定式化と塑性オプション
- 大変形 / 微小ひずみ
- インターフェース(/INTER/TYPE7)
金属帯とローラーの間の接触はTYPE7インターフェースでモデル化されます。メインサーフェスはローラーの外表面で、セカンダリ節点は金属帯(/GRNOD/PART)で定義されます。ローラーの幅方向には1要素しかありません。前のインターフェースは対称として扱う必要がありません。ギャップには人為的に1 mmが選択されます。
- 境界条件(/BCS)
金属帯の下側の節点は(移動機械ベッドを表現するため)Z方向に拘束されます。
ローラーのメイン節点はX軸周りの回転を除いて全ての方向が拘束されます。
- 一定時間ステップ(/DT/BRICK/CST)
- 強制速度(/IMPVEL)
両方のローラーのメイン節点のX軸周りに一定角速度が与えられます。
- 初速(/INIVOL)
金属帯の全ての節点のX方向に初速度500 mm/sが与えられます。
- 弾塑性材料則(/MAT/LAW2 (PLAS_JOHNS))
- 一般的なソリッドプロパティ(/PROP/TYPE14(SOLID))
- 剛体(/RBODY)
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
単位: mm、s、Mg、N、 MPa
この解析ではレールの圧延のフェーズを示します。ブランク材が連続的にその厚さを減らす目的で通過します。両方のローラーは一定角速度6.85 rad/sを持ち、金属帯は機械カーペットによって引き込まれます。このプロセスは準-静的と考えることができ、高い変形を含みます(主に圧縮)。
- 材料特性
- 初期密度
- 7.8 x 109 Mg/mm3
- ヤング率
- 210000
- ポアソン比
- 0.3
- 降伏応力
- 170
- 硬化パラメータ
- 400
- 硬化指数
- 0.475
- パラメータ
- 温度指数
- 1
- 溶融温度
- 2073 K (およそ1800°C)
- 定圧における熱容量Cp
- 460
- 形状
- 金属帯の断面は80 x 20 mmであり、ローラーの半径は100 mmです。1つ目のローラーの通過後には板厚は7 mmだけ薄くなり、2つ目のローラーの通過後には板厚はさらに5 mmだけ薄くなります。
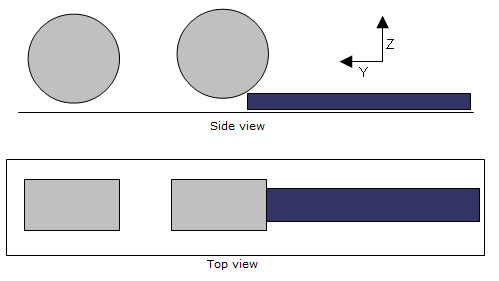
図 2. 問題の形状
モデリング手法
金属帯の幅方向には多くの要素は必要なく、むしろ板厚方向の応力分布を正確に得るため、金属帯の板厚方向に少なくとも5要素は必要になります。何に着目するかには依存しますが、板厚方向の5要素は十分な多さかもしれません。この問題は解析の初期の部分で議論されるべきです。ローラーに関しては、要素は1次であるため曲率を完全にモデル化するのは簡単ではありません。そのメッシュは曲率を可能な限り正確に見積もるのには十分に細かい必要があり、幅方向は1要素で十分です。
詳細: 移動する機械ベッドはモデル化されず、金属帯の全ての下側の節点はZ方向に拘束されます。加えて、最初のローラーとの接触が開始されるため金属帯に初速度が与えられます。金属帯とローラーの間には摩擦係数0.3を用いたCoulomb摩擦仮定し、これで金属帯がローラーに引き込まれます。
ローラーは剛であると仮定し、そのメイン節点に一定回転速度が与えられます。
結果
板厚方向の要素数
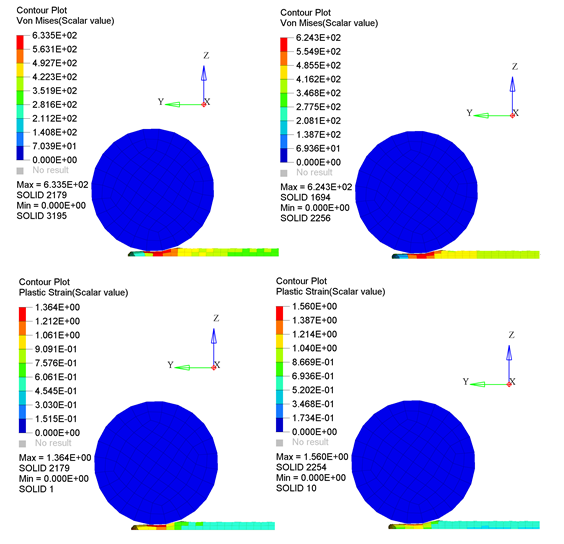
図 3. 2要素と5要素の比較
応力(またはひずみ)分布を見るには、厚さ方向に対して2要素では不十分で、5要素あれば十分なように見えます。変形形状がスムーズでない、あるいは2要素間の勾配が高すぎる場合、メッシュの再分割を考えますが、そうでない場合にはややコストがかかりすぎる可能性があります。加えて、厚さ方向5要素ではモデルの実行に時間が12倍かかっています。
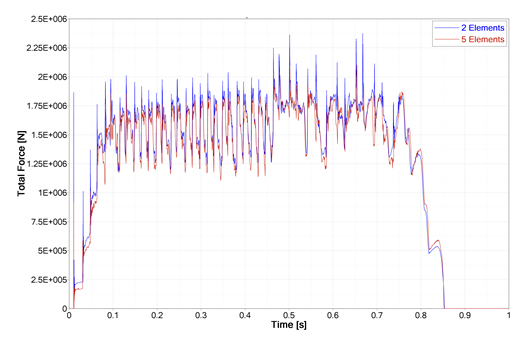
図 4. 円柱に作用する反力
上のグラフは厚さ方向に2要素と5要素を用いた場合の最初の円柱に作用する反力を示したものです。両方の曲線はほとんど同じで、5要素を使用した場合、より長い計算時間が必要とされます。したがって、CPU時間を節約するため、2要素以上を用いる必要はないことになります。
微小ひずみ定式化の影響
通常、大変形を含む問題では、大ひずみ定式化が用いられるかも知れません。Radiossでは、これがデフォルトの設定ですが、微小ひずみ定式化を用いることも可能です。この定式化は大変形に対してあまり正確ではありませんが、よりロバストで、時間ステップの落ち込みが大きくなりすぎないようにすることができます。実際、大変形 / 回転問題では時間ステップの大きな落ち込みを起こすようなメッシュのゆがみを生じ、計算が負の体積で止まることすらあります。微小ひずみ定式化では一定体積を仮定することによりこれら全てを克服して時間ステップは一定になり、メッシュが完全にゆがんだ場合でも計算が負の体積により止まることはありません。
この定式化はフラグIsmstrに1を特定のパートのタイプに直接与えることにより、t=0から適用させることができます。これは、Engineファイル(*_0001.rad)の/DT/BRICK/CSTオプションを用いて限界時間ステップを持たせることで、シミュレーションの間に負の体積を防止するため、あるいは時間ステップの低下を維持するために、大ひずみ定式化から微小ひずみ定式化に切り替えることもできます。
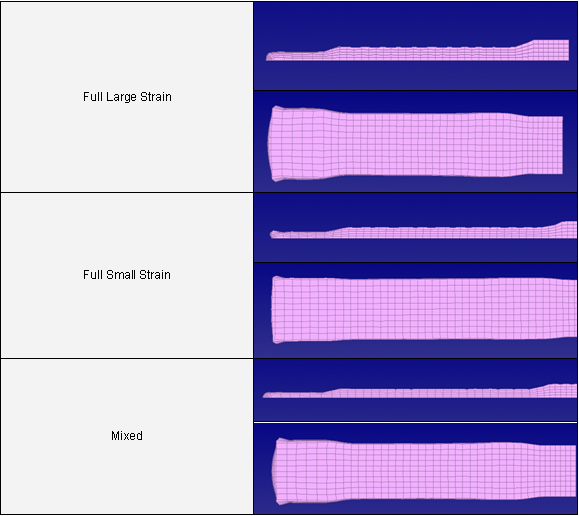
図 5. 変形形状
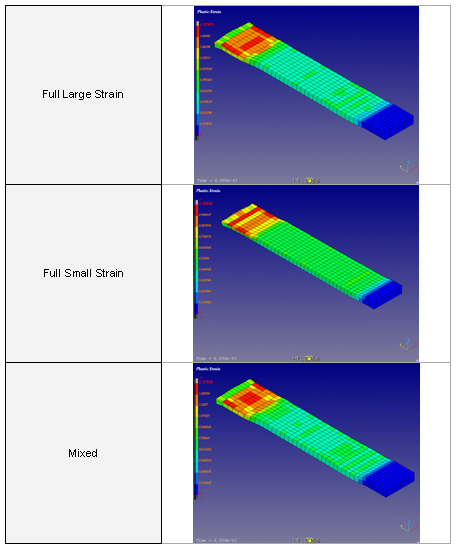
図 6. 変形形状
このような場合に微小ひずみ定式化を用いることは興味のあることかも知れません。ただし、ゆがんだ1つの要素のために時間ステップが止まるわけではありませんが、少数の要素だけが限界時間ステップに達しています(/DT/NODA/CSTを用いて)。しかしながら、精度の理由からは、微小ひずみに切り替わる要素の数はチェックされるべきで、少ない程良いことになります。
HA8定式化の影響
改良されたHA8ソリッド定式化は標準の8積分点の定式化(Isolid=17または14)の欠点を克服しています。特に、純粋な伸びでの、“せん断ロッキング”(標準の定式化でやや硬くなる)が存在しません。微小ひずみ定式化を用いることも可能で、これは反対に8積分点の定式化では適合しません。ここではそれぞれの方向に対して9点までの積分点を用いることも可能になりました。
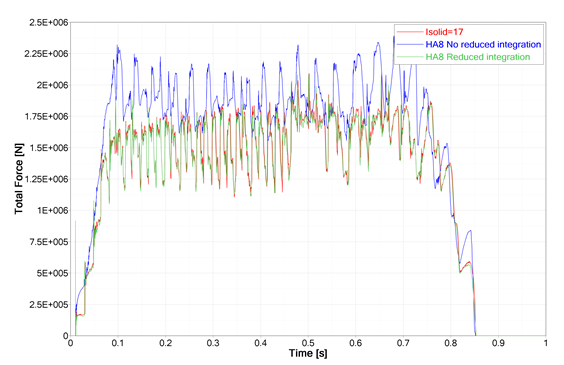
図 7. 異なる定式化でのローラーの力
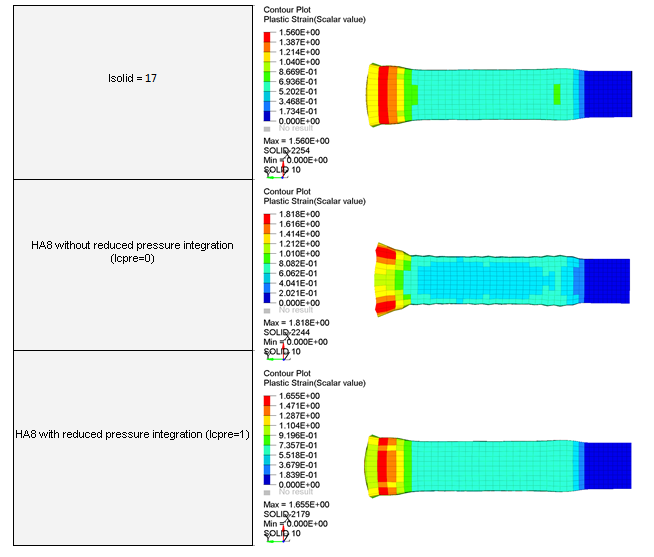
図 8. 異なる定式化での塑性ひずみ
HA8定式化では、実際冷厳圧力積分と共に用いられる必要があり、厚肉シェルを8節点ソリッドでエミュレートする場合のみこのオプションを非アクティブにする必要があります。
温度の影響
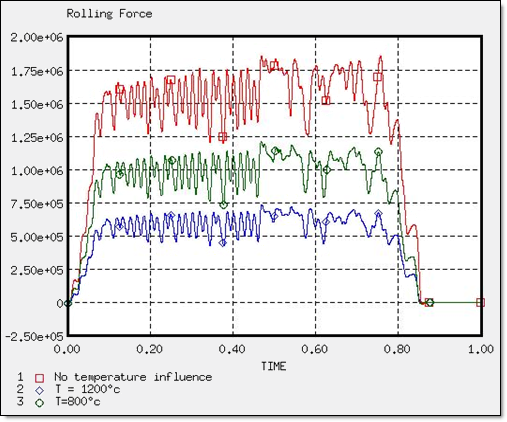
図 9. ローラーの力
まとめ
Radiossによる2つの転がる円柱の下でのスチールベルトの押し潰しがシミュレートされています。大変形定式化で十分な数の要素を用いた時、物理的に受け入れられる結果を得ることが可能になっています。微小ひずみ定式化は悪い結果を引き起こしていますが、低コストです。要素定式化と板厚方向の積分点数は結果に影響する他のパラメータで、高い精度は、高いコストとなります。これに対して、問題は準-静的と考えられるので、Radioss陰解法ソルバーを考えることもできます。