RD-E:2700 サッカーのシュート
サッカーボールがゴールポストにぶつかるシミュレーション

図 1.
これはデモ用の例題です。1976年の欧州サッカー選手権決勝戦、バイエルンミュンヘン(FC Bayern Munich)対サンテティエンヌ(AS St. Etienne)で、フランスチームの2本のシュートが敵方のゴールポストに跳ね返されました。実際、ヨーロッパの国の中でイングランドだけがゴールポストを丸いポールに置き換えておらず、このことがフランスのサポーター達に、もしゴールポストが置き換えられていたらサンテティエンヌは決勝で勝てたはずだと信じさせることになります。シミュレーションに基づき、これらの疑いに対する答えが与えられるはずですが、議論はこれからも明らかに続きます。
使用されるオプションとキーワード
- 4-節点シェル(Q4)と3-節点シェル(T3)、弾性直交異方性シェルの繊維則
- 注入気体の混合入力を使用した単室型エアバッグ(/MONVOL/AIRBAG1)
- センサー(/SENSOR)
- 剛体(/RWALL)(剛性円筒および剛性平行四辺形)
- 剛体(/RBODY)
- 初速度(/INIVEL)
- 与えられた座標系での節点グループに対する並進および回転速度(/INIVEL/AXIS)
- 並進材料速度(/INIVEL/TRA)
- 節点グループに対する重力荷重(/GRAV)
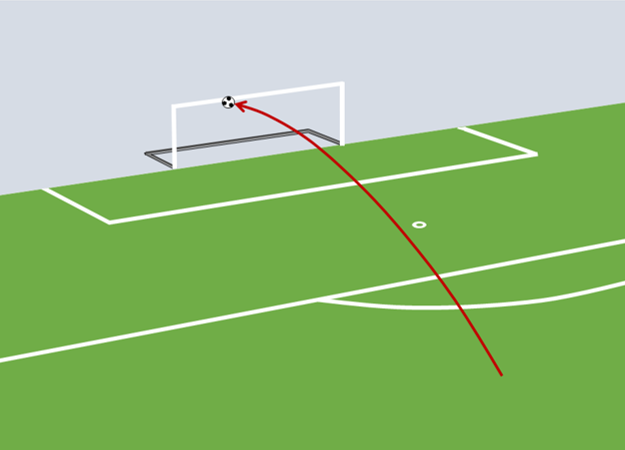
図 2. Bathenayのシュートのボールの軌跡
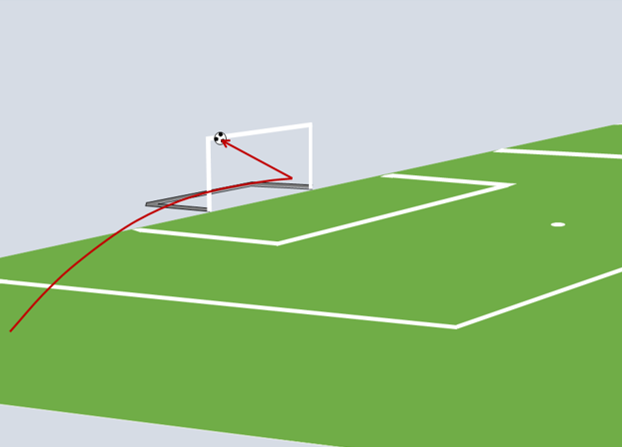
図 3. Santiniのヘッディングのボールの軌跡
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
1976年の欧州サッカー選手権決勝戦(バイエルンミュンヘン対サンテティエンヌ)で、BathenayのシュートとSantiniのヘディングが、ドイツチームのゴールの正方形断面のフレームに跳ね返されました。このデモの目的は、正方形断面と円形断面の両方のケースの影響を特定することにあります。
両方のシュートの間の違いは、発生率、速度とボールのバーへの衝撃位置(鉛直位置)です。
- 初期密度
- 2.01x10-3
- ヤング率(方向1、2)
- 20000
- せん断弾性係数(12、23、31)
- 10000
- ポアソン比
- 0.29
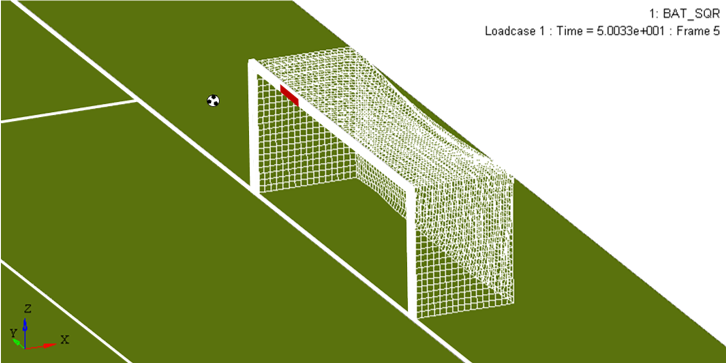
図 4. 問題の形状
モデリングの方法
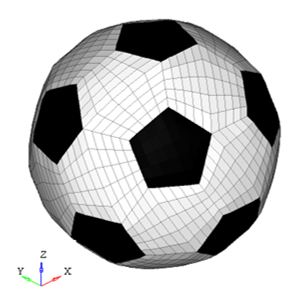
図 5. ボールのメッシュ
使用されるRadiossオプション
- ボールの全ての節点を含む1つの剛体が生成されます。これはバーに衝突する直前に非アクティブにされます。
- 回転および並進初速が/INIVEL/AXISを用いて剛体のメイン節点に与えられます。速度は、/FRAME/FIXを用いて局所座標系で定義されます。
- ゴールポストは、丸いポストに対しては円筒剛壁が、四角いポストに対しては2つの剛な平行四辺形が用いられます。
- 重力荷重を用いて重力が考慮されます。
- ボールはエアバッグとして考慮され、剛体が非アクティブ化されたときにアクティブ化されます。
複数のEngineファイルが使用されます。2つ目のEngineは、/RBODY/OFFを用いてボール剛体を非アクティブ化します。時間のアニメーション出力は1 ms毎に増やされるため、ボールがゴールにぶつかる詳細を見ることができます。3つ目のEngineファイルは、アニメーション出力を12.5 ms毎に戻します。
結果
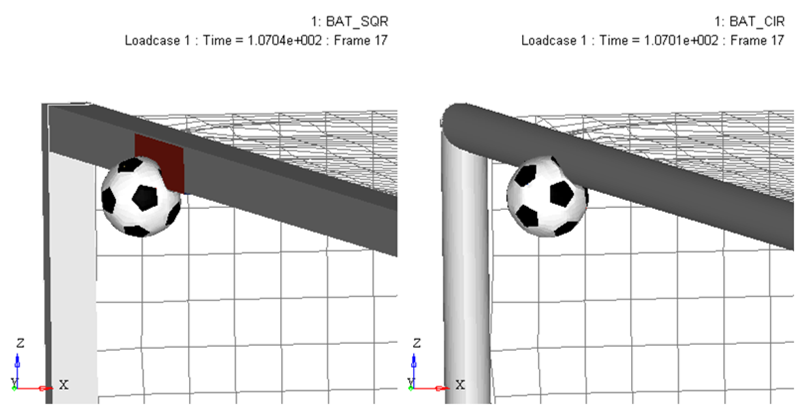
図 6. 正方形断面と円形断面へのサッカーボールの衝撃
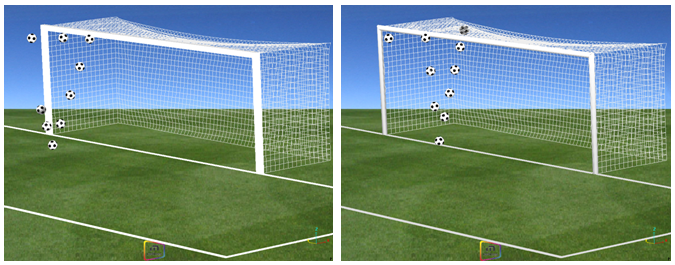
図 7. Bathenayのシュートのボールの軌跡. (それぞれ四角いバーと丸いバーへの衝撃)
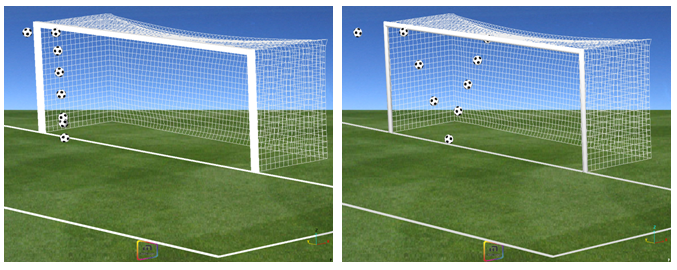
図 8. Santiniのヘッディングのボールの軌跡. (それぞれ四角いバーと丸いバーへの衝撃)
まとめ
衝撃の単純なモデル化を用いているにも関わらず(バーはパートの代わりに剛壁でモデル化)、正方形断面のケースの結果のシミュレーションは実際と比較した時に非常に正確な結果をもたらしています。円形断面のバーで得られた結果は、両方のシュートがゴール内に入ることを示しています。しかしながら、摩擦や回転速度といった多くの衝撃のパラメータは正方形断面ケースのキャリブレーションで推定されています。