RD-E:1000: 曲げ
3節点および4節点シェル定式化での純曲げテスト

図 1.
使用されるオプションとキーワード
梁の1つの端部は全ての自由度が拘束されます。反対側に置かれた剛体のメイン節点に回転速度が課されます。
図 2. 梁のメッシュ
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
この例題の目的は、純曲げ問題を検討することです。端部へのモーメントの片持ち梁が検討されます。自由端への一定強制速度でモーメント変化がモデル化されます。
以下の単位系が用いられます: mm, ms, g, N, MPa
複数の種類の要素定式化が用いられます。
- 材料特性
- 初期密度
- 0.01
- 参照密度
- .01
- ヤング率
- 1000
- ポアソン比
- 0
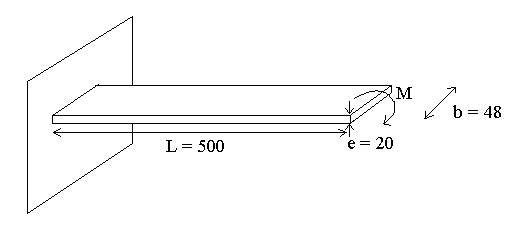
図 3. 問題の形状
モデリング手法
- Belytshcko&Tsay定式化でのQ4メッシュ(Ishell=1, アワグラスタイプ 1, 2, 3)
- QEPH定式化でのQ4メッシュ(Ishelll=24)
- QBAT定式化でのQ4メッシュ(Ishelll=12)
- DKT18定式化でのT3メッシュ(Ishell=12)
結果
数値結果と解析解との比較
図 3に示すように、自由端のX軸周りの回転とY方向変位が検討されます。
以下の表に異なる定式化で得られた結果をまとめます。解析的視点から、純曲げを受ける梁は一定の曲率で = の条件を満足する必要があり、梁は閉じた輪を形成するはずです。しかしながら、用いた要素定式化によっては、以下の表に示したような多少の誤差が見受けられます。これは主に、非常にフレキシブルであるための梁の変形の間の振動によるものです。良い結果は、それぞれQBAT、QEPH と DKT18 要素で得られています。これは主に、これらの要素定式化での曲率の良い見積もりによるものです。低減積分要素の BT ファミリーの精度は低くなっています。タイプ3アワグラス定式化では、モデルは = 6radまで安定を保っています。しかし、モーメント-回転の曲線は期待された応答に一致していません。
全体の計算誤差を減らすため、より小さい時間ステップが/DTでのスケールファクターを減らすことにより用いられます。最後の表で報告された結果は、BT要素での発散の問題は避けられないものの、時間ステップの減少が誤差の累積の減少を可能にすることを示しています。
| BATOZ | QEPH | BT | DKT | |
|---|---|---|---|---|
| スケールファクター | 0.6 | 0.9 | 0.9 | 0.2 |
| 強制回転速度 | 0.005 rad/ms | 0.005 rad/ms | 0.005 rad/ms | 0.005 rad/ms |
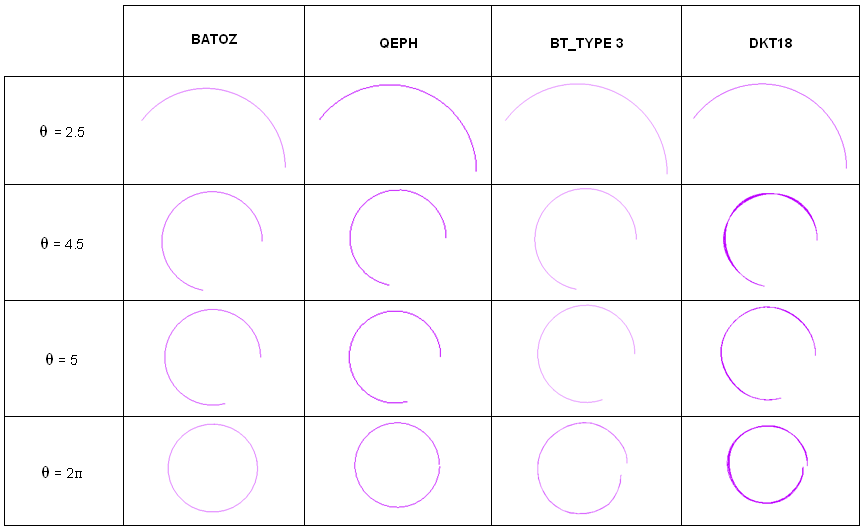
図 4.
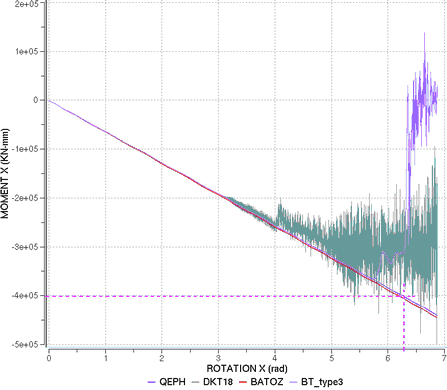
図 5. モーメント対X軸周りの回転
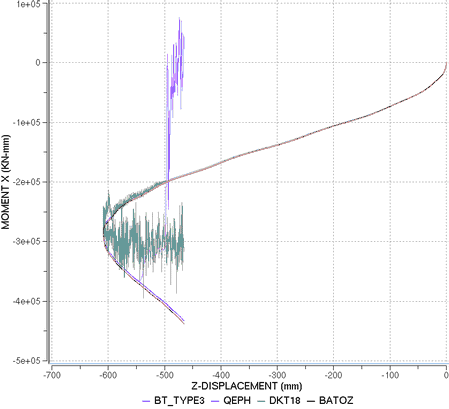
図 6. モーメント対Z方向変位
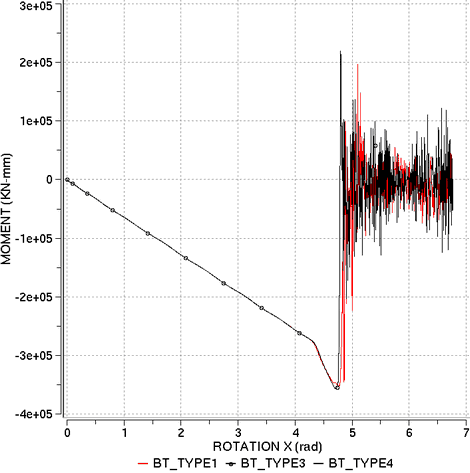
図 7. モーメント対X軸周りの回転
| BATOZ | QEPH | BT | DKT | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sf=0.9 | Sf =0.8 | Sf =0.6 | Sf =0.9 | Sf =0.8 | TYPE1 | TYPE3 | TYPE4 | Sf =0.3 | Sf =0.2 | Sf =0.1 | ||||
| Sf =0.9 | Sf =0.1 | Sf =0.9 | Sf =0.1 | Sf =0.9 | Sf =0.1 | |||||||||
| CPU (正規化) # サイクル |
2.18 97600 |
2.43 109800 |
3.14 146400 |
1.23 95800 |
1.34 107800 |
42.64 59100 |
7.07 552600 |
2.62 182300 |
108.60 -- |
1.03 59100 |
7.17 552600 |
5.44 364100 |
8.21 621600 |
16.21 1243200 |
| 誤差 = 2 (%) |
0% | 0% | 0% | 0% | 0% | 55.3% | 99% | 0% | 0% | 55.9% | 99.9% | 3.4% | 28.88% | 3.7% |
| err =20% (rad) 発散 |
6.91 396° |
6.89 395° |
-- | -- | -- | 4.36 250° |
4.53 260° |
6.06 347° |
5.98 343° |
4.38 251° |
4.51 258° |
6.37 365° |
-- | -- |
| Dz = 2 (mm) |
-500.5 | -500.5 | -500.5 | -500.5 | -500.5 | -491.2 | -525.8 | -518.333 | -506.0 | -529.8 | -433.8 | -476.5 | -496.5 | -499.4 |
| Mx = 2 (x10+5kN-mm) |
-4.04 | -4.05 | -4.06 | -4.01 | -4.01 | -0.21 | -0.11 | -3.13 | -2.38 | -0.07 | -0.02 | -3.09 | -3.02 |
-3.08 |
まとめ
- QBAT要素
- この定式化では梁の-回転をエネルギーエラーなしで与えます。しかし、 = 384度で20%の誤差に達しています。
- QEPH要素
- この定式化はこの問題を取り扱うには最も良いかと思われます。これは、-回転を得ることを可能にしています。誤差は = 400°まで0になっています。
- BT定式化
- この定式化は、どのアンチアワグラス定式化を用い場合でも満足する結果を与えず、このシミュレーションには適していません。これは主に平板の定式化を用いていることによるものと、要素が低減積分されている事実によるものですTYPE3アワグラス定式化が他よりも良いと思われます。
- DKT定式化
- 曲げは正確にシミュレートされています。しかし、要素のコストが高く、CPU 時間がずっと長くなっています。