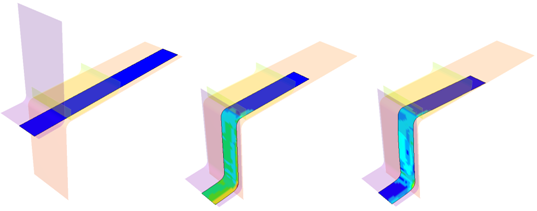
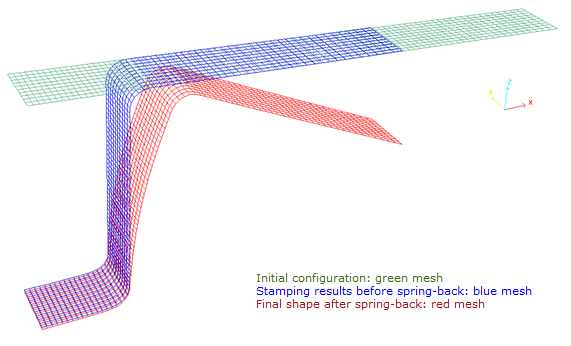
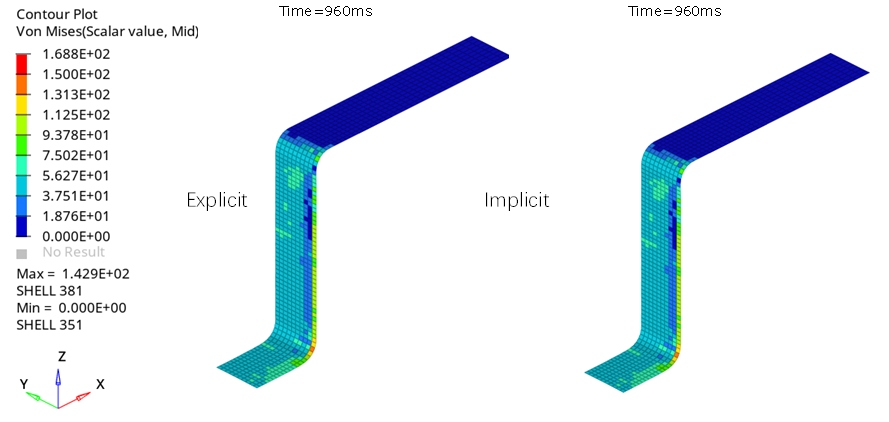
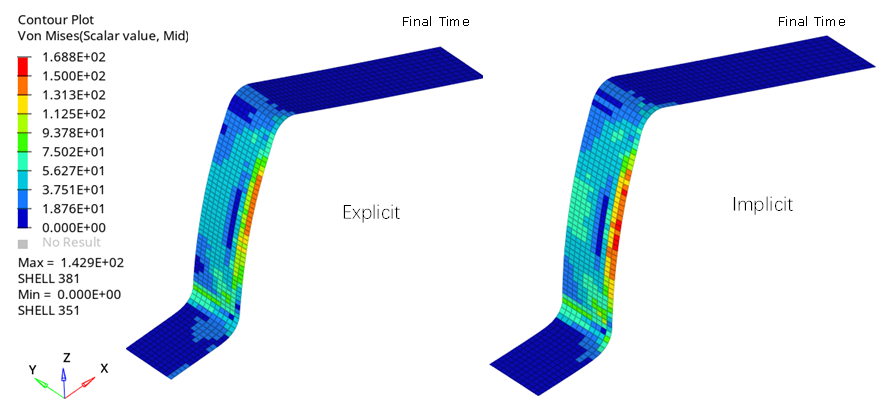
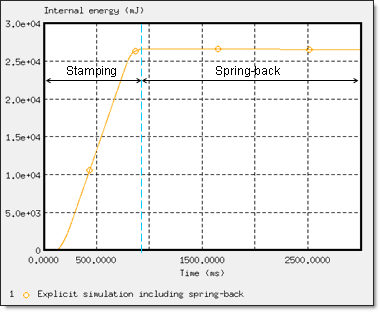
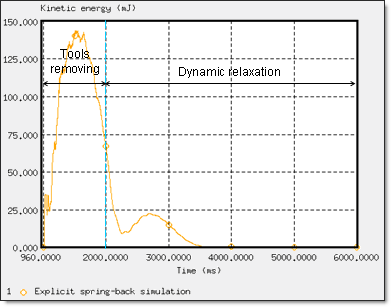
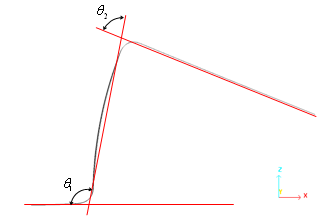
この例題ではスプリングバックを含むスタンピングプロセスの数値シミュレーションを扱います。
これは、Numisheet’93で示されている金属シートスンピングテストの1つである”2D Draw Bending”を指します。ブランクシート上の全ての拘束が解放された後の、形成された金属シートの最終形状が検討されます。スプリングバックシミュレーションの間、陽解法から陰解法への連続解法が用いられ、最初に動的な成形では陽解法が、続く成形の応力を静的に取り除くスプリングバック変形では陰解法でのモデル化が用いられます。
2つの解析がパフォーマンスと解析精度を比較するために実行されます:
- 陽解法スタンピングと陰解法スプリングバックシミュレーション
- 陽解法スタンピングと(動的緩和を用いた)陽解法スプリングバックシミュレーション
金属シート成形のスプリングバックシミュレーションでは弾塑性非線形アプローチが用いられます。陰解法入力オプションと用いられた増分ストラテジーはモデリングのセクションで記述されます。
スタンピングの数値シミュレーションは960 msまで実行されます。スプリングバック計算は960 msから1000 msが陰解法(静解析アプローチ)で、6000 msまで陽解法(準-静的アプローチ)で実行されます。
標準的なスタンピング工程が検討されます。スタンピングツールにはパンチ、ダイとフランクフォルダが含まれます。
単位: mm、ms、g、N、 MPa。
金属シートをダイに対して固定するために荷重1225 Nがブランクフォルダに鉛直に与えられます。荷重はスプリングバックシミュレーションの前に取り除かれます。
金属シートスタンピング工程は最大0.1 ms
-1に設定されたパンチに作用する変化する強制速度を用いて管理されます。ツールはスタンピングフェーズの後で観察するスプリングバックが可能になるように取り払われます。
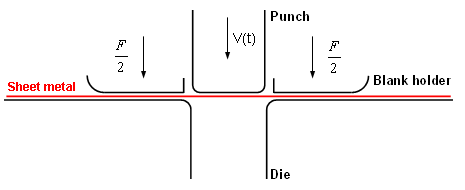
図 2. 問題の概要
パートの主な寸法は:
- ダイのコーナーの半径
- 5 mm
- パンチのコーナーの半径
- 5 mm
- パンチ幅
- 50.4 mm
- 金属シートの寸法
- 35 mm x 175 mm
金属シートの板厚は0.74 mmで定義されます。 金属シートとダイの間のCoulomb摩擦係数は0.129で定義されます。
スタンピングツールの材料は以下の線形則の下で行われます:
- 材料特性
- 初期密度
- 8x10-3
- ヤング率
- 206000
- ポアソン比
- 0.3
圧延を受ける金属シートの材料は特別な異方性の特性を持っています。異方性弾塑性挙動はHillモデル(/MAT/LAW43)で導入できます。この材料則は、von Mises降伏条件の異方性降伏挙動への一般化と考えることができます。
降伏応力はユーザー関数により定義され、降伏応力は相当応力と比較されます:(1)
係数が、Lankford異方性パラメーターの範囲を用いて決められます。ランクフォードパラメータの角度は、直交異方性方向1に対して定義されます。
|
|
|
|
|
|
硬化係数が硬化モデルを完全な等方性(値を0にセット)またはPrager-Ziegler移動硬化モデル(値を1にセット)として記述するために用いられます。係数の値が0と1の間の場合には硬化は2つのモデルの間で補間されます。
- 材料特性
- 初期密度
- 8x10-3
- モデルで80を使用すると計算が速くなります。
- ヤング率
- 206000
- ポアソン比
- 0.3
- 0°のランクフォード
- r00 = 1.73
- 45°のランクフォード
- r45 = 1.34
- 90°のランクフォード
- r90 = 2.24
用いられた降伏曲線を
図 3に示します:破壊は考慮されません。
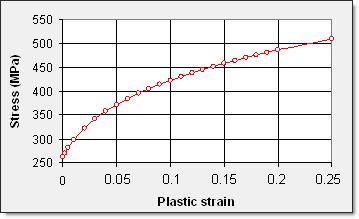
図 3. ユーザー降伏関数
シミュレーションの反復
対称性を考慮して、構造の1/4がモデル化されます。対称平面は軸y = 17.5 mmとx = 0 mmです。
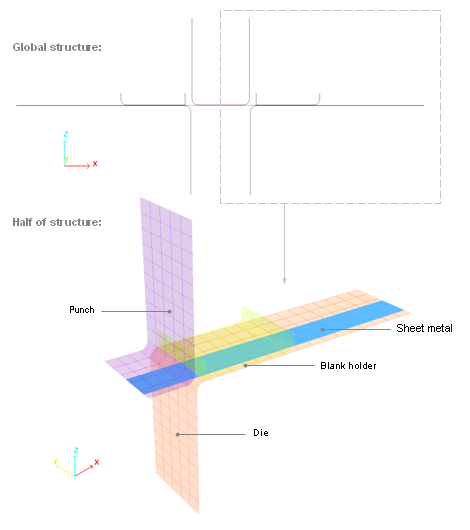
図 4. 検討された問題の有限要素メッシュ
パンチは紫で、ブランクフォルダは緑で、ダイは赤で示されています。金属シート(青)は4節点シェル要素を用いてモデル化されています。
金属シートは非均一なメッシュで離散かされ、塑性変形するパートに対して細かいメッシュが用いられます。シェル要素の最小メッシュサイズは1.5 mmです。

図 5. 金属シートの漸変メッシュ
精度の良いシミュレーション結果を達成するため、QEPHシェル要素定式化が陽解法と陰解法解析に用いられます。Lagrange定式化が適用されます。
材料則の弾塑性Hillモデルに対応して、金属シートは直交異方性プロパティ(TYPE9)を用いたシェル要素で記述されます。シェルの特性は:
- 5 積分点(漸進塑性化)
- 3 Newton反復での反復塑性(Iplas = 1)
- 応力計算に板厚変化を考慮(Ithick = 1)
- 初期板厚は0.74mmの一定値
- 直交異方性の角度: 0 度。
- 参照ベクトル: (1 0 0)
参照ベクトルの入力成分は直交異方性の局所座標系の方向1の定義に用いられます。度単位の直交異方性角度は直交異方性の方向1とシェルへの投影ベクトルとの間の角度を定義します。
ペナルティ法を用いた3つのTYPE7インターフェースがスタンピングツールと金属シートの間に使用されます。接触を定義するパラメーターは:
- 材料特性
- Coulomb摩擦
- 0.129
- Gapmin
- 0.37
- 面剛性の臨界減衰係数
- 1
- インターフェース摩擦の臨界減衰係数
- 1(デフォルト)
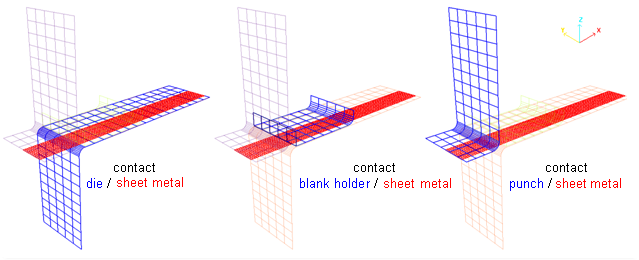
図 6. ペナルティ法のタイプ 7インターフェースを用いた接触のモデル化(マスター / スレーブ側)
陰解法アプローチでは、ペナルティ法の仮想スプリングを用いた接触はメインとは別の剛性マトリックスに保存されます。したがって、追加のメモリが必要で、接触がアクティブになった時に2番目の接触剛性の情報が印刷されます。
臨界減衰係数(入力)の記述:
- 法線方向力計算は次のように示されます: (2)
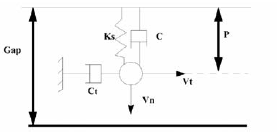
図 7.
ここで、
- 初期インターフェーススプリング剛性
- インターフェース剛性の臨界減衰係数(デフォルト値: 0.05)
- 接線方向力計算は次のように示されます:(3)
ここで、
- インターフェース摩擦の臨界減衰係数(デフォルト値: 1)
陰解法でのスプリングバック計算ではスタンピングツールの除去を、次のような2番目の
*_0002.rad Engineファイルの入力においての全てのインターフェースの削除で考慮します:
/DEL/INTER
1 2 3
インターフェースID 1、2、3が削除されます。
シミュレーションは以下で取り扱われます:
- 陽解法によるスタンピングシミュレーション:最初から960 msまで。
- スプリングバックシミュレーション:
- 陽解法を使用(動的アプローチ):960 msから6000 msまで。
- 960 msから6000 msまで: スプリングバック時の動的効果を最小化するために準-静的解析が必要なために、スタンピングツールはゆっくりと取り除かれます。ここでは、インターフェースは削除されません。オプションは*_0002.rad Engineファイルで定義されます。
- 2000 msから6000 msまで:準-静的つり合いに収束させるため動的緩和(/DYREL)が*_0003.rad Engineファイルでアクティブ化されます。
- 陰解法を使用(静的アプローチ):960 msから1000 msまで:
- 入力の陰解法オプションは *_0002.rad Engineファイルに加えられます。応力緩和は/IMPL/SPRBACKキーワードを用いてアクティブ化されます。全てのインターフェースは削除され、スタンピングツール上に特定の境界条件が加えられます。ツールは取り払われません。
シミュレーションでは、
図 8に示すように、ツールは剛体(
/RBODY)を用いてモデル化されます。
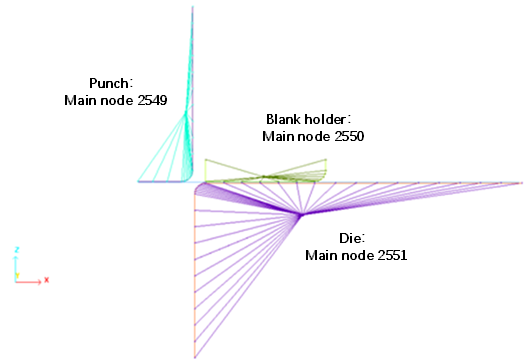
図 8. スタンピングツールの剛体要素でのモデル化
自動メイン節点が選択されています。重心がメイン節点とセカンダリ節点の座標から計算され、メイン節点は質量と慣性が置かれる重心位置に移動されます(ICoGは1にセット)。質量と慣性は剛体には付加されません。
モデルサイズを制限し、陰解法計算での剛体モードをなくすため、構造の1/4がモデル化されます。対称平面がy 軸 = 0に沿って定義されます。
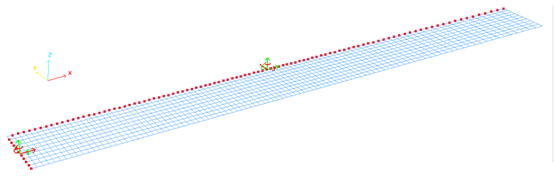
図 9. 対称条件による金属シートの境界条件(/BCS)
長さ方向平面上の節点はY並進方向とX、Z軸周りの回転が拘束されます。
他の対称平面では、X並進方向とY、Z軸周りの回転が拘束されます。
スタンピングツールは移動がZ軸に沿ってのみに制限されます。境界条件は、パートを含む剛体のメイン節点に与えられます(図 9)。
陰解法スプリングバックの数値シミュレーションでは、陰解法アプローチでは許されない剛体モードを除去するため付加的な条件が
*_0002.rad Engineファイルに追加される必要があります。スタンピングツールは完全に拘束されます(X、Y、Z並進方向とX、Y、Z軸周り回転)。節点ID 427のZ軸に方向の並進の拘束で金属シートは最終形状に剛体モード無しに移動できるようになります。
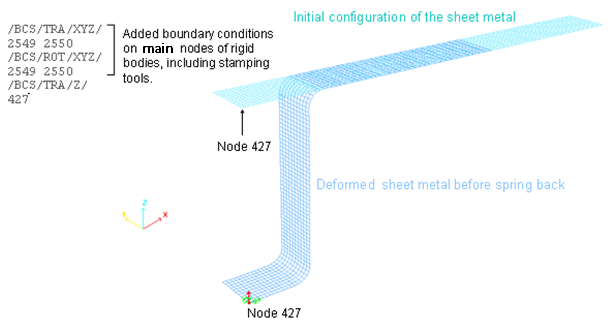
図 10. 陰解法スプリングバックでの節点 427 への付加的境界条件
スタンピングツールへの強制速度が剛体のメイン節点を通して与えられます。パンチの速度は、
図 11と
図 12に示した特定の入力曲線で制御されます。陰解法スプリングバックの間は全ての速度は0に設定されます。6000 msまでの陽解法スプリングバック計算では1000 msでツールを取り除くための強制速度がツールに課されます。
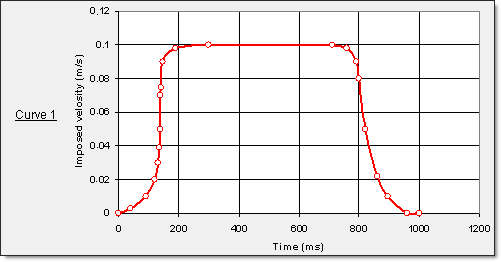
図 11. 剛体のマスター節点を通して与えられるパンチの強制速度
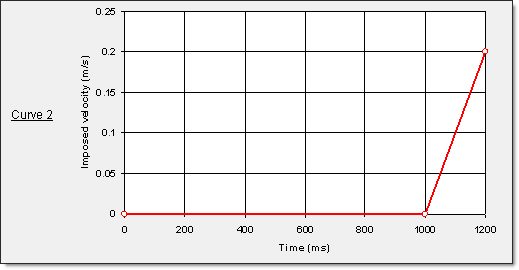
図 12. 剛体のマスター節点を通して与えられるダイとブランクフォルダの強制速度
" パンチパート・・・曲線 1、スケールファクターは-1に設定。
" ダイパート・・・曲線 2、スケールファクターは1に設定。
" ブランクフォルダパート・・・曲線 2、スケールファクターは-1に設定。
スタンピングは、曲線1を用いて960msまで陽解法シミュレーションによって実行されます。陰解法シミュレーションは、960 msから1000 msまでのスプリングバックステージのみについて実行されます。このため曲線2は、陽解法スプリングバックシミュレーションに対してのみ定義されています。
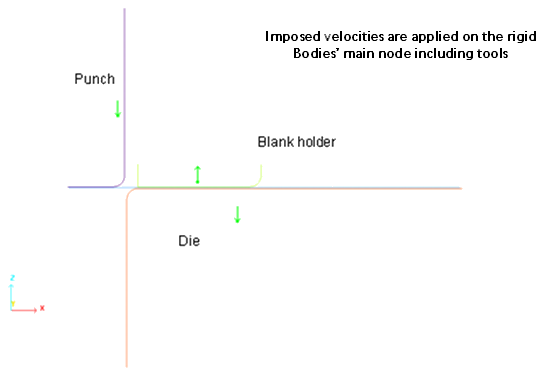
図 13. スタンピングおよびツールの除去という2つのフェーズにおけるツールに対する強制速度
対称性を考慮して、一定の集中荷重612.5 Nが鉛直に剛体のメイン節点を通してブランクフォルダに与えられます。荷重はスプリングバックが検討される前の0から960 msに設定されます。
陰解法スプリングバック解析は /IMPL/SPRBACKキーワードを用いて起動されます。
用いられた非線形陰解法パラメーターは:
/IMPL/NONLIN/1
#L_A Itol Toli Tolj Tolk
2 0 0.025
|
- 陰解法タイプ
- 静的非線形
- 非線形ソルバー
- N=1
- 修正Newton
- 収束判定基準
- Toli=0.025
- 剛性マトリックスの更新
- L_A=2
- 最大反復回数
|
/IMPL/DTINI
0.08
|
- 初期時間ステップ
- 0.08 ms
|
/IMPL/DT/STOP
# DT_MIN DT_MAX
1e-5 0.0
|
- 最小時間ステップ
- DT_MIN=10-5 ms
- 最大時間ステップ
- なし
|
/IMPL/DT/2
#lt_w L_arc L_dtn dt_sca dt_sca_max
6 0.0 20 0.67 0.0
|
- 時間ステップコントロール法
- 変位のノルム(孤長)
- 望ましい収束の反復回数
- It_w=6
- 収束の最大反復回数
- L_dtn=20
- 時間ステップ減少係数
- dt_sca=0.67
- 最大時間ステップ増加係数
- dt_sca_max=0.0
- 孤長
- L_arc=0
- 自動計算
|
/IMPL/SPRBACK
|
- スプリングバックオプション
- アクティブ
|
それぞれの非線形反復サイクルでAx=bを解くソルバーの手法が必要です。これはオプション/IMPL/SOLVERで定義されます。
入力の陰解法オプションは
*_0002.rad Engineファイルに加えられます。
/IMPL/SOLVER/2
# Iprec It_max Itol Tol
5 0 0 0.
|
- 線形ソルバーの解法
- N=2
- 直接法ソルバーMUMPS
- 前処理法
- Icpre=5
- 因子化された近似逆行列
- 最大反復回数
- It_max=0
- 系の次元(NDOF)
- 終了基準
- Itol=0
- マトリックスの相対残差
- 終了基準の収束判定
- Tol=0
- マシンの精度
|
陰解法オプションの詳細についてはRadioss Starter入力をご参照ください。
陽解法スプリングバック解析は*_0003.rad Engineファイルで2000 msから動的緩和を用います。
陽解法積分スキームは節点加速度の計算から始まります。これは動的荷重のシミュレーションには効率的です。しかし、動的解法を通した準-静的解析では、静的つり合いの解に収束させるために動的効果を最小化することが必要で、これによりスプリングバック後の最終形状が達成されます。
動的緩和では、質量マトリックスに比例する対角減衰マトリックスを導入することにより、動的効果が減衰されます。
(4)
(5)
ここで、
- 推奨されるデフォルト値を擁する緩和の値
- 減衰される期間(系の最長期間以下)
動的緩和の入力値は:
- リラクゼーション係数
- 1
- 減衰時間
- 1000 ms
このオプションは/DYRELキーワードでアクティブになります(入力: および)。
/ADYRELキーワードを使用した場合、パラメータは自動的にRadiossで計算されるため、入力は不要です。