この例題の目的は、Altair Radiossを使用した摩擦メカニズムのシミュレーションの紹介です。
単位: kg、mm、ms、GPa
このブレーキシステムは、2つのブレーキパッドに挟まれた1枚のディスクで構成されています。このディスクの半径は100mm、幅は50mm、厚みは5mm、質量は0.914kgであり、各ブレーキパッドの厚みは5mm、重さは0.06kgです。これらのパートは、HEPH(Isolid=24)要素定式化を使用した3次元ソリッド要素でモデル化します。
このディスクの初期回転速度はです。この初期回転速度は、/INIVEL/AXISキーワードを使用して定義します。この結果、慣性として5712.5kg/mm2が得られます。このディスクの内径の内側に1つの剛体を作成します。この剛体のメイン節点は回転の中心であり、Y軸を中心とした回転を除くすべての自由度が拘束されています。
各ブレーキパッドの外面上に1つの剛体を作成します。ブレーキ操作をシミュレートするために、2つのブレーキパッドに結合した各剛体のメイン節点に0.3kNの集中荷重が作用するようにします。その結果、これらのブレーキパッドがディスクの各面と接触します。
ディスクとパッド間の接触は、サーフェス間接触
/INTER/TYPE19を使用してモデル化されます。ここでは、摩擦によって生じた熱をエネルギーに変換することを可能にする熱接触フラグがアクティブ化されます。0.3というクーロン摩擦係数が接触インターフェースで設定されます。
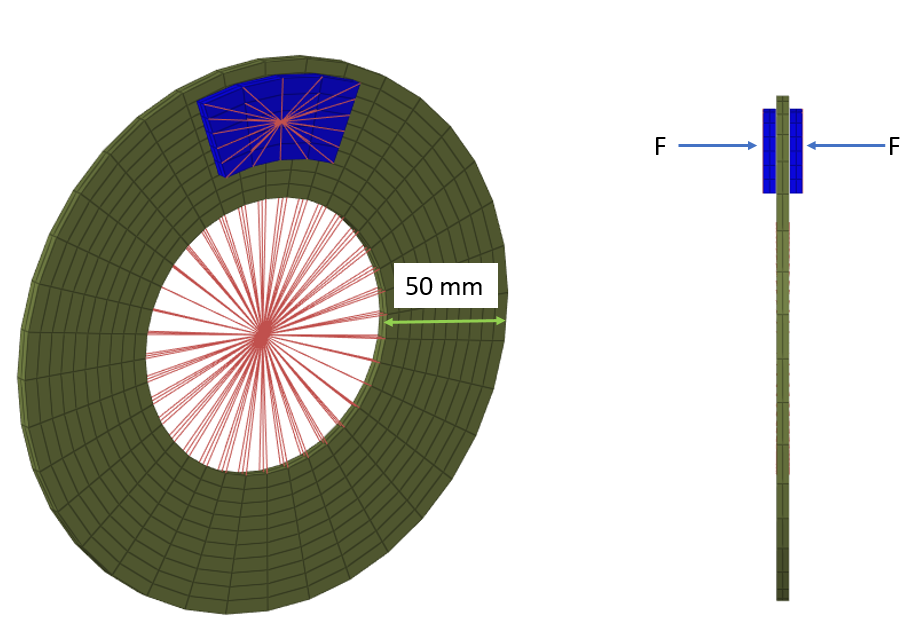
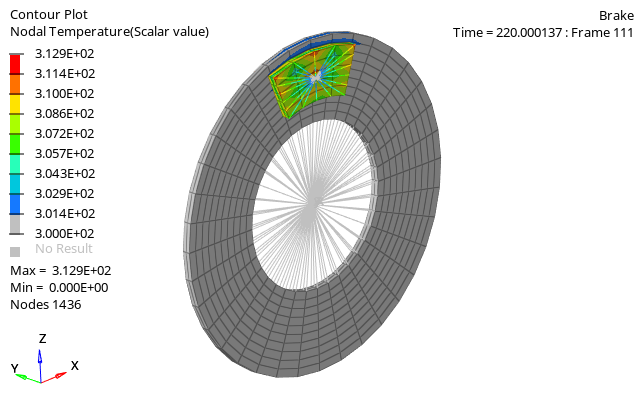
図 2. ブレーキモデル
ディスクとブレーキパッドに使用している材料モデルは、Johnson-Cook塑性モデルを使用した等方性弾塑性則(/MAT/LAW2)です。ディスクとブレーキパッドの間の熱伝導をモデル化するには、材料の熱パラメータを/HEAT/MATで設定して、/MAT/LAW2材料と同じmat_IDを使用する必要があります。材料で/HEAT/MATを使用する場合は、/MAT/LAW2に設定した熱パラメータではなく、/HEAT/MATに入力したパラメータを使用します。
このディスクは、次の熱パラメータにより、一般的なスチール材料のプロパティを使用してモデル化されています:
- 材料特性
- 初期温度
- 300
- 単位体積あたりの比熱()
- 0.00244
- 固体相の熱伝導係数A
- 0.02
- Lagrange熱伝導定式化
- Iform=1
- 溶融温度
- 2000
ブレーキパッドの材料プロパティと熱プロパティは次のとおりです:
- 材料特性
- 初期密度
- 7.3 e-06
- ヤング率
- 160
- ポアソン比
- 0.3
- 初期温度
- 300
- 単位体積あたりの比熱()
- 0.004
- 固体相の熱伝導係数A
- 0.02
- Lagrange熱伝導定式化
- Iform=1
- 溶融温度
- 2000