表面状態 (仕上げと処理)
疲労破壊が表面から発生するとき、表面状態は疲労強度に影響を与える極端に重要な因子となります。表面仕上げと処理係数が疲労解析結果の補正として考慮されます。
表面仕上げ係数
が、表面の粗さを特性化するために用いられます。これは、研磨、機械加工、鍛造といった定性的な条件でカテゴリー分けされた仕上げの図に表されています。
1

図 1. 鋼材の表面仕上げ補正係数
表面処理は部材の疲労強度を改善させることができます。NITRIDED(窒素化)、 SHOT-PEENED(ショットピーニング)、COLD-ROLLED(冷延)は表面処理補正として考慮されます。値を入力して表面処理係数
を指定することもできます。
一般的な場合、全補正係数は
処理タイプがNITRIDEDの場合、全補正整数は、
。
処理タイプがSHOT-PEENEDまたはCOLD-ROLLEDの場合、全補正整数は、
= 1.0。これは表面仕上げの効果を無視する事を意味します。
疲労耐力限界FLは、
により
。2セグメントのS-N曲線では、遷移点の応力も、
を掛けることにより修正されます。
表面状態は、PFATバルクデータエントリで定義することができます。続いて、表面状態は、モデル部分にFATDEFバルクデータエントリを通して関連付けられます。
疲労強度減少係数
上で述べた係数に加えて、様々な他の因子が構造の疲労強度に影響を与える可能性があります。例えば、切欠き効果、寸法効果、荷重タイプ等です。疲労強度減少係数
はこのような補正を一体化して考慮するものとして導入されます。疲労耐力限界FLは、
により
疲労強度減少係数は、PFATバルクデータエントリで定義することができます。続いて、モデル部分にFATDEFバルクデータエントリを通して関連付けられます。
と
の両方が指定された場合、疲労耐久限界FLは、
と
は、その弾性部分がS-N定式化上にあることを通して、E-N定式化でも同様の影響を持ちます。E-N定式化の弾性部分では、公称疲労耐力限界FLがNcの弾性限界から内部的に計算されます。FLは、
と
がある場合には修正されます。その弾性部分は送信された公称疲労限界とともに修正されます。
疲労材料データにおけるばらつき
S-NおよびE-N曲線 (およびその他の疲労特性) は、完全反転の回転曲げ試験を通して、実験から得られます。通常実験結果には大きなばらつきを伴うため、データの統計的な特徴づけが必要になります(曲線の標準
誤差による平均 log(N) の最も悪い値の推定には耐久確実性が用いられ、より高い信頼性レベルにはより大きな耐久確実性を必要とします)。
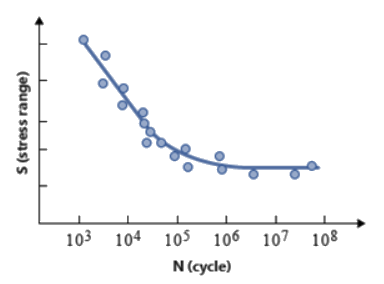
図 2. ばらつきデータのあるS-N曲線
これらのパラメータを理解するために、1つの例としてS-N曲線を考えましょう。S-N実験データが、公称応力の大きさSaまたは範囲SRのどちらかに対する破壊のサイクル数Nが共に対数でプロットされると、そのSとNの関係は直線のセグメントで記述できます。通常、1つまたは2つのセグメントでの理想化が用いられます。
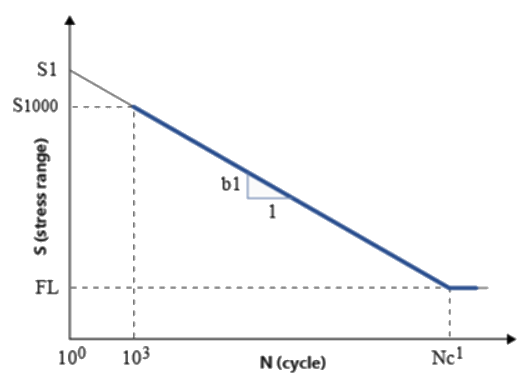
図 3. 両対数スケールでの1セグメントS-N曲線
S-Nのばらつきにより、同じ材料の同じサンプル試験体で、見込まれるS-N曲線に差が生じる状況について考えましょう。自然なばらつきにより、完全反転の回転曲げ試験の結果は、通常、応力範囲(S)と寿命(N)の両方のデータポイントでばらつきが生じます。対数スケールで見ると、Log (S)とLog (N)にばらつきがあります。具体的には、同じ応力範囲が与えられた場合の寿命のばらつきを見ると、データポイントは次のようになります。
| S |
2000.0 |
2000.0 |
2000.0 |
2000.0 |
2000.0 |
2000.0 |
| Log (S) |
3.3 |
3.3 |
3.3 |
3.3 |
3.3 |
3.3 |
| Log (N) |
3.9 |
3.7 |
3.75 |
3.79 |
3.87 |
3.9 |
多くのプロセスと同様に、Log (N)の分布は正規分布とみなされます。
log (S)の特定の値には、 log (N)の可能な値がすべて含まれています。この完全な母集団セットの平均は真の母集団の平均であり、未知です。したがって、サンプルの(MATFATのSN カーブ)およびStandard Error(MATFATのSE)のユーザー入力サンプル平均 SN カーブに基づいて、log(N)の最悪の真の母集団平均値を統計的に推定します。MATFATエントリに入力される SN 材料データは、データの生成に使用される特定のユーザーサンプルにおけるばらつきの通常分布の平均に基づいています。
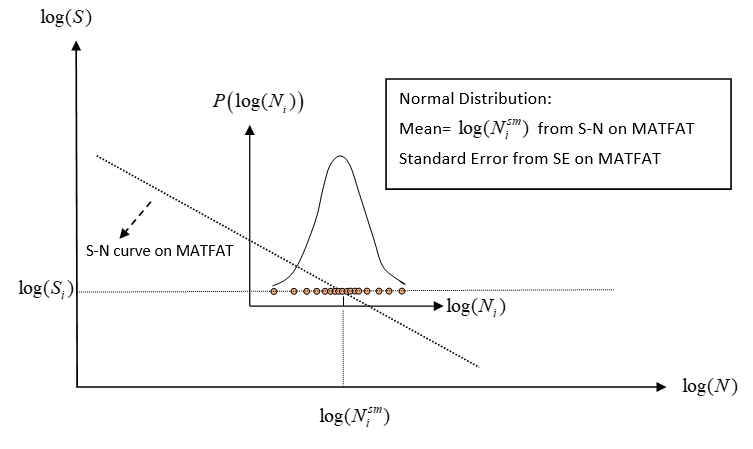
図 4. S-NのばらつきのLog (N)分布の確率関数. 特定のユーザー定義サンプルデータ
応力範囲と寿命の両方のデータに実験的なばらつきが存在します。MATFATエントリでは、log(N)のばらつきの標準誤差が入力(S-N曲線のSEフィールド)として必要です。サンプル平均は、 S-N曲線により
として与えられ、MATFATエントリのSEフィールドを使用して入力されます。
指定されたS-N曲線が摂動なしに直接使用される場合、各データポイントでの正規分布の平均値が使用されるものとみなされ、デフォルトでは耐久確実性が50%となります。これは、
OptiStructは、
MATFATエントリでユーザーが指定したサンプル平均を変更しないことを意味します。耐久確実性50%という値は、すべての用途で十分な値とは限らないため、
OptiStructでは、ユーザーが定義した必要な耐久確実性となるように内部的にS-N材料データに摂動を与えることができます。このためには、次のデータが必要となります。
- log (N)の正規分布の標準偏差(標準誤差)(MATFATのSE)
- 本解析に要するCertainty of Survival(FATPARMのSURVCERT)。
正規分布またはガウス分布は確率密度関数であり、曲線の下の全面積は常に1.0になります。
ユーザー定義のSN曲線データは、正規分布であると想定されます。一般的には、次の確率密度関数表されます。
(1)
ここで、
-
- データ値
はユーザーサンプル。
-
- サンプル平均
。
-
- 不明なサンプルの標準偏差(MATFAT標準誤差(SE)のみのユーザー入力)。
で。
上記の分布はユーザー定義サンプルの分布であり、完全な母集団空間ではありません。真の母集団平均は未知であるため、サンプル平均とサンプルSE から真の母集団の平均値の推定範囲を求め、その後ユーザーが指定した耐久確実性(SURVCERT)を使用して、サンプル平均を抽出します。
標準誤差は、全母集団から抽出されたサンプルのすべてのサンプル手段によって作成される正規分布の標準偏差です。1つのサンプル分布データから、標準誤差は通常、
と推定されます、ここで
は、サンプルの標準偏差で、
はサンプルのデータ数です。すべてのサンプル平均におけるこの分布の平均は、実際には真の母集団の平均と同じです。ユーザーにより与えられる耐久確実性は、すべてのサンプル平均のこの分布に適用されます。
一般的には、正規分布関数を標準正規分布曲線(平均=0.0、標準誤差=1.0の正規分布)に変換します。これにより、Zテーブルを介して耐久確実性を直接利用することができます。
注: 耐久確実性は、確率密度関数の必要なサンプルポイント間の曲線の下の面積に等しくなります。正規分布曲線の下の面積を直接(標準正規分布曲線に変換せずに)計算することは可能ですが、参照用の標準正規分布表に比べて計算の負荷が大きくなります。したがって、一般的に使用されている方法では、まず現在の正規分布を標準正規分布に変換してから、標準正規分布表を使用して入力した耐久確実性をパラメータ化します。
すべてのサンプル平均の通常の分布では、この分布の平均
は実際の母集団の平均と同じであり、その範囲が推定対象となります。
統計的に、真の母集団の平均の範囲を次のように推定できます。
(2)
つまり、
(3)
左側の値はより保守性が高いので、次の式を使用してSN曲線を変化させます。
(4)
ここで、
-
- 摂動値
-
- ユーザー指定のサンプル平均( MATFATのSN曲線)
-
- 標準誤差( MATFATのSE)
の値は耐久確実性の入力値に基づいて標準正規分布Zテーブルから求められる。以下に、該当する耐久確実性の典型的なZの値をいくつか示します。
- Z値(計算値)
- 耐久確実性(入力値)
- 0.0
- 50.0
- 0.5
- 69.0
- 1.0
- 84.0
- 1.5
- 93.0
- 2.0
- 97.7
- 3.0
- 99.9
上記の例(S-N)に基づいて、S-N曲線が必要な耐久確実性と標準誤差の入力に変更される様子がわかります。このテクニックにより、統計的手法を使用して疲労材料データのばらつきを処理し、必要な耐久確率値のデータを予測することができます。



