応力勾配効果は、FKMガイドライン法または臨界距離法のいずれかの方法で考慮することができます。
これは、シェル要素およびソリッド要素の両方でサポートされています。ソリッド要素の場合、静解析結果を用いた疲労解析では節点応力でしか応力勾配効果が得られません。応力勾配効果がアクティブになっている際、ソリッド要素の場合、 FATPARMのSURFSTSフィールドは自動的にGPに設定されます。
応力勾配法は、単一軸および多軸SN、EN、FOS疲労に対応しています。溶接、振動および過渡疲労解析ではサポートされていません。
FKMガイドライン法
FKMガイドライン法では、FKMガイドラインのルールを用いて計算した係数で疲労強度を増加させることで応力勾配効果が考慮されます。FKMガイドライン法のOptiStruct実装では、各時間ステップにおける応力テンソルの6成分をFKMガイドラインで規定された係数で低減しています。
FKMガイドライン法を用いて応力勾配効果をアクティブにするには、FATPARMのGRDフィールドをGRDFKMに設定する必要があります。
応力勾配効果を考慮してサーフェスの応力を低減するためには、以下の手順を踏む必要があります。
- 応力テンソル
の6成分の応力勾配を、応力履歴の線形結合後の各時間ステップで計算します。z方向は外向きの面法線です。ソリッド要素の場合、サーフェスの応力とサーフェスから1mm下の応力との有限差分で勾配を計算します。サーフェスから1mm下の応力は、対象とする要素の節点応力から補間された応力です。2次ソリッド要素の場合、コーナー部の節点応力のみが補間に使用されます。シェル要素の場合は、両層の応力とその板厚から勾配が計算されます。
- Step 1で得られた応力勾配を用いて、各時間ステップでサーフェス法線方向の等価応力勾配
が解析的に計算されます。等価応力は、フォンミーゼス応力または絶対最大主応力のいずれかです。
- 関連する応力勾配
は、以下の正規化を用いて計算されます。(1)
- 補正係数
を計算します。補正係数の計算をご参照ください。
- 補正係数
をサーフェス応力テンソルに適用し、サーフェス応力を低減します。非線形解析でEN疲労解析を行う場合、対応するひずみテンソルに同じ
を適用することで、低減されたひずみテンソルを得ることができます。(2)
補正係数の計算
補正係数の計算は、FKMに記されている
と
の間の関係に基づいています。
FKMガイドラインによると、応力補正係数
は次のように計算されます:
-
-
-
表 1. 値の例 -- 定数
および
| 定数 |
ステンレススチール |
その他のスチール |
GS |
GGG |
GT |
GG |
展伸アルミニウム合金 |
鋳造アルミニウム合金 |
|
|
0.40 |
0.50 |
0.25 |
0.05 |
-0.05 |
-0.05 |
0.05 |
-0.05 |
|
|
2400 |
2700 |
2000 |
3200 |
3200 |
3200 |
850 |
3200 |
ここで、
- GS
- 鋳鋼と熱処理可能な一般用鋳鋼
- GGG
- ノジュラー鋳鉄
- GT
- 可鍛鋳鉄
- GG
- ラメラグラファイト鋳鉄(グレー鋳鉄)
は MPaでUTS、
の寸法はmmです。OptiStructは、 MATFATで定義された応力単位とFATPARMで定義された応力単位と長さ単位を介して、
と
の単位系を管理します。
と
の値は、キーワードSTSGRDの後にMATFATでユーザーが入力した値です。応力勾配はmmの長さ寸法で計算しなければならないため、OptiStructがサーフェスから1mm下の点を正しく見つけることができるように長さの単位を定義します。
が負である場合、
は1.0に設定されます。
が100 mm-1より大きい場合、
は1.0に設定され、警告メッセージが示されます。
ユーザー定義の関係
と
の間のユーザー定義の関係は、 TABLES1バルクデータを介して指定することができます。ペア(xi,yi) = (
,
)は、TABLES1エントリで定義できます。
と
の間の関係を定義するTABLES1は、キーワードSTSGRDの後にMATFATで参照されなければなりません。
がxiの範囲外にある場合、外挿の挙動は通常のTABLES1の挙動に従います。つまり、
は、
が負である際に
が負または100mm-1以上であるときにどのように扱われるかによって、1.0よりも低くなることがあり得ます。ユーザー定義の関係は、FKMガイドラインのものよりも優先されます。
臨界距離法
臨界距離法を用いて応力勾配効果をアクティブにするには、FATPARMのGRDフィールドをGRDCDに設定する必要があります。
微小応力集中フィーチャーまたは高い応力勾配を持つ形状は、同じ最大応力を持つより大きなフィーチャーまたはより小さい勾配よりも疲労に効果を及ぼしません。たとえば0.1mmほどの小さな穴のあるプレートは、同じ応力集中係数と最大応力を持っているにもかかわらず、10mmの大きな穴のあるプレートよりもはるかに長い疲労寿命を示します。従来の疲労解析では、応力集中係数
Ktではなく、経験的な疲労ノッチ係数
Kfを用いて応力勾配効果を考慮しています。有限要素モデルには
Ktや公称応力の概念がないため、応力勾配の影響を直接考慮します。すべての穴には同じ最大応力があり、公称応力の3倍です。
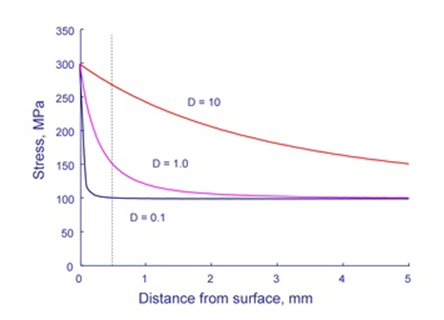
図 1. 穴の大きさが異なる3種類のプレートの応力分布
図 1 に示すように、応力は穴の端部のみで大きさに依存せず、穴から遠く離れたところで変化しています。図中の破線は0.5mmで描いています。ここでは、穴の大きさが大きくなるにつれて応力が大きくなります。亀裂核生成メカニズムにより、大きさ0.5mmの亀裂が発生したとします。最小の0.1mmの穴では、成長を続けるために利用可能な応力は公称応力である100MPaしかありません。同じ大きさの亀裂には、大きい方の穴に275MPaの応力がかかり、最大応力とほぼ同等です。
大きさの異なる穴の周りの亀裂の核生成には、亀裂核生成のためのプロセスゾーンを考えることが有用です。材料は、亀裂核生成メカニズムが作用するサイズスケールでは連続的かつ均質ではありません。材料の粒度は、疲労プロセスゾーンを可視化するのに便利な方法です。
図 2 は、
図 1からの応力分布に粒子サイズを重ね合わせたものです。プロセスゾーンの応力は何でしょうか?簡単な第一近似では、粒の中心部の応力を取ることになります。したがって、10mm穴の場合は275MPaの応力で、0.1mm穴の場合は100MPaの応力で疲労寿命を計算することになります。
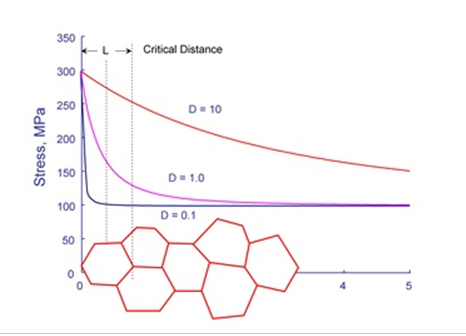
図 2.
現代の疲労の考えでは、材料が疲労限界で応力を受けると、マイクロ亀裂は形成されるが、プロセスゾーンの外では成長しないとされています。応力勾配効果は、非常にシンプルでわかりやすい方法で疲労解析に含まれています。臨界距離法では、サーフェスの応力とひずみではなく、サーフェスからの距離L/2(ポイント法)での応力とひずみを使用します。ソリッド要素の場合、サーフェス下L/2での応力とひずみは、対象の要素の節点応力とひずみから補間した応力、ひずみです。2次ソリッド要素の場合、コーナー部の節点応力のみが補間に使用されます。
臨界距離は、しきい値応力強度
と疲労限界範囲
で次のように表すことができます:
(3)
臨界距離は材料固有の特性です。使用中の材料の臨界距離がわかっている場合は、キーワード
STSGRDの後に
MATFATに臨界距離を入力することができます。臨界距離を入力する際には、
MATFATでも長さの寸法を定義することが重要です。しかし、特に微小なマイクロ亀裂の場合、しきい値応力強度が未知の場合が多いため、しきい応力強度からの臨界距離を計算することは困難となります。幸いなことに、臨界距離と疲労との間には良好な直接の相関関係があります。
(4)
臨界距離を直接入力しない場合、OptiStructはSN疲労解析で式 4を使用して臨界距離を推定します。疲労限界
は、SN曲線調整後に取得します。Lの寸法はmmです。
EN疲労解析では、疲労限界
は次のように近似しています。
(5)
(6)
ここで、
-
- 疲労強度係数。
-
- 反転耐久限界。
-
- ヤング率。
が0、または
が0.2mmより大きい場合、
は0.2mmに設定されます。シェル要素の場合、計算される最大値
は、板厚/4です。
応力勾配効果を有効にするための入力
FATPARMのキーワードSTRESSの後のGRDフィールドで使用する方法(FKMガイドライン法または臨界距離法)を選択します。FKMガイドライン法を選択した場合は、FATPARMのSCBFKMフィールドに、応力勾配を計算するための等価応力
法を指定する必要があります。応力勾配効果に必要な材料特性は、MATFATのキーワードSTSGRDの後に入力します。

