軌跡の検討
ボールの挙動は、
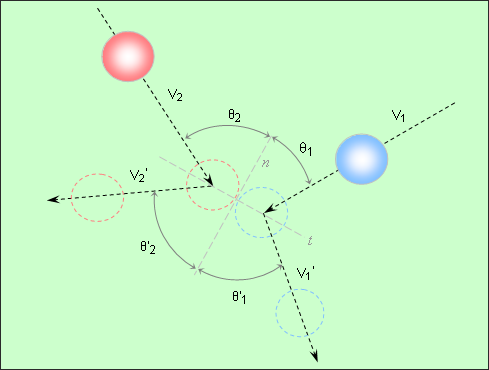
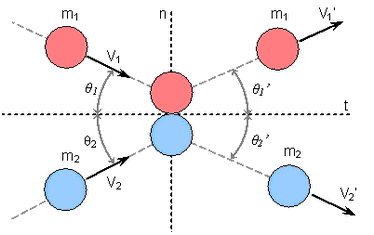
図 1 に示すパラメーター(角度と速度)を用いて表現されます。数値結果は、完全な弾性反発を前提として(反発係数は1)、解析解と比較されます。
図 1. 問題のデータ
初期値 V1
0.7m.s-1
V2
1m.s-1
θ
1 40°
θ
2 30
massball
44.514g
モデリング手法
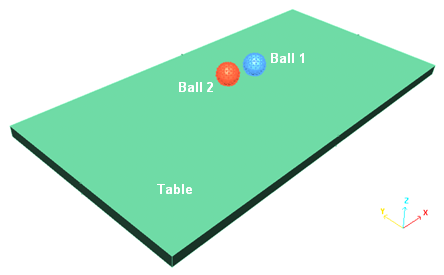
ボールとテーブルは前のプールゲームの定義と同じプロパティを持ちます。テーブルの寸法は 900 mm x 450 mm x 25 mmでボールの直径は50.8 mmです。 ボールとテーブルはTYPE16 Lagrangeインターフェースを用いるために16節点厚肉シェル要素でメッシングされます。
図 2. 問題のメッシュ(16節点厚肉シェル)
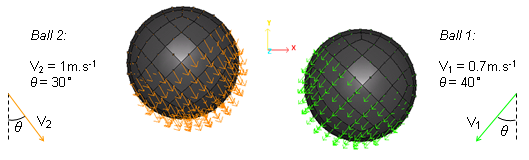
初期並進速度がボールに
/INIV Engine オプションを通して与えられます。速度はXとY軸に投影されます。
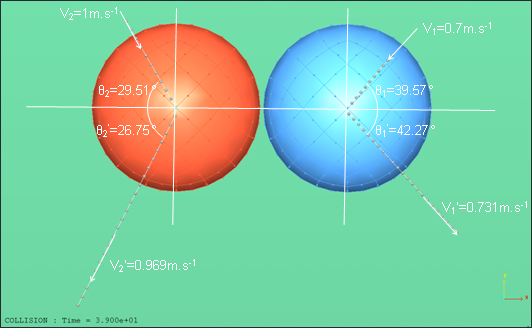
図 3. ボールに与えられた初速度(初期位置)
ボールには重力が考慮されます(0.00981 mm.ms-2 )。
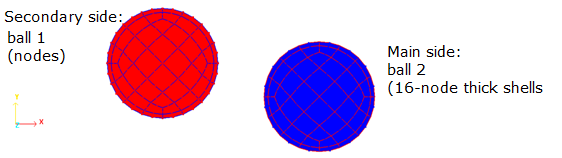
ボール-ボールとボール-テーブルの接触はTYPE16インターフェース(セカンダリ節点 / メイン16節点厚肉シェル接触)を用いてモデル化されます。ボール / ボール接触のインターフェース定義を
図 4 に示します。
図 4. TYPE16 Lagrangeインターフェースのメインとセカンダリ側
解析解
1と2の2つのボールを置き、質量は
m
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGTbWaaSbaaSqaaiaaigdaaeqaaaaa@3AB0@
と
m
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGTbWaaSbaaSqaaiaaigdaaeqaaaaa@3AB0@
とし、同じ平面内を移動してそれぞれが衝突のコースで速度
V
1
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGTbWaaSbaaSqaaiaaigdaaeqaaaaa@3AB0@
と
V
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGTbWaaSbaaSqaaiaaigdaaeqaaaaa@3AB0@
で、に示すように接近します。
図 5. 2つのボールの衝突の一般的問題
速度は局所軸
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGUbaaaa@39CA@
と
t
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGUbaaaa@39CA@
に投影されます。速度と、衝突後の速度の方向を取得するために、運動量保存則が2つのボールについて記録されます:
(1)
−
m
1
V
1
n
+
m
2
V
2
n
=
m
1
V
1
n
'
−
m
2
V
2
n
'
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqGHsislcaWGTbWaaSbaaSqaaiaaigdaaeqaaOGaamOvamaaBaaa
leaacaaIXaGaamOBaaqabaGccqGHRaWkcaWGTbWaaSbaaSqaaiaaik
daaeqaaOGaamOvamaaBaaaleaacaaIYaGaamOBaaqabaGccqGH9aqp
caWGTbWaaSbaaSqaaiaaigdaaeqaaOGaamOvamaaDaaaleaacaaIXa
GaamOBaaqaaiaacEcaaaGccqGHsislcaWGTbWaaSbaaSqaaiaaikda
aeqaaOGaamOvamaaDaaaleaacaaIYaGaamOBaaqaaiaacEcaaaaaaa@5073@
または
(2)
−
m
1
V
1
sin
θ
1
+
m
2
V
2
sin
θ
2
=
m
1
V
1
'
sin
θ
1
'
−
m
2
V
2
'
sin
θ
2
'
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqGHsislcaWGTbWaaSbaaSqaaiaaigdaaeqaaOGaamOvamaaBaaa
leaacaaIXaaabeaakiGacohacaGGPbGaaiOBaiabeI7aXnaaBaaale
aacaaIXaaabeaakiabgUcaRiaad2gadaWgaaWcbaGaaGOmaaqabaGc
caWGwbWaaSbaaSqaaiaaikdaaeqaaOGaci4CaiaacMgacaGGUbGaeq
iUde3aaSbaaSqaaiaaikdaaeqaaOGaeyypa0JaamyBamaaBaaaleaa
caaIXaaabeaakiaadAfadaqhaaWcbaGaaGymaaqaaiaacEcaaaGcci
GGZbGaaiyAaiaac6gacqaH4oqCdaqhaaWcbaGaaGymaaqaaiaacEca
aaGccqGHsislcaWGTbWaaSbaaSqaaiaaikdaaeqaaOGaamOvamaaDa
aaleaacaaIYaaabaGaai4jaaaakiGacohacaGGPbGaaiOBaiabeI7a
XnaaDaaaleaacaaIYaaabaGaai4jaaaaaaa@63FD@
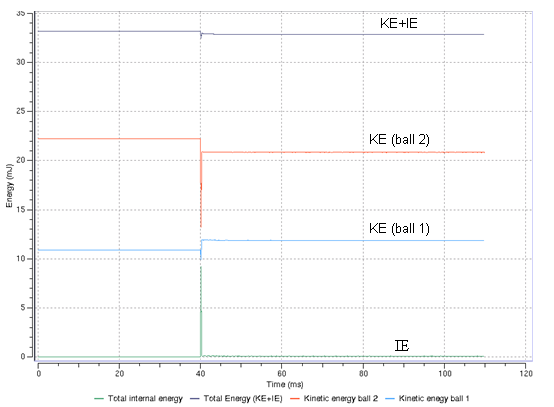
衝撃波弾性で摩擦無しと仮定されます。並進運動エネルギーの維持が尊重され、回転エネルギーは考慮されないとすると:
(3)
1
2
m
1
(
V
1
n
'
2
+
V
1
t
'
2
)
+
1
2
m
2
(
V
2
n
'
2
+
V
2
t
'
2
)
=
1
2
m
1
(
V
1
n
2
+
V
1
t
2
)
+
1
2
m
2
(
V
2
n
2
+
V
2
t
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaWcaaqaaiaaigdaaeaacaaIYaaaaiaad2gadaWgaaWcbaGaaGym
aaqabaGcdaqadaqaaiaadAfadaqhaaWcbaGaaGymaiaad6gaaeaaca
GGNaGaaGOmaaaakiabgUcaRiaadAfadaqhaaWcbaGaaGymaiaadsha
aeaacaGGNaGaaGOmaaaaaOGaayjkaiaawMcaaiabgUcaRmaalaaaba
GaaGymaaqaaiaaikdaaaGaamyBamaaBaaaleaacaaIYaaabeaakmaa
bmaabaGaamOvamaaDaaaleaacaaIYaGaamOBaaqaaiaacEcacaaIYa
aaaOGaey4kaSIaamOvamaaDaaaleaacaaIYaGaamiDaaqaaiaacEca
caaIYaaaaaGccaGLOaGaayzkaaGaeyypa0ZaaSaaaeaacaaIXaaaba
GaaGOmaaaacaWGTbWaaSbaaSqaaiaaigdaaeqaaOWaaeWaaeaacaWG
wbWaa0baaSqaaiaaigdacaWGUbaabaGaaGOmaaaakiabgUcaRiaadA
fadaqhaaWcbaGaaGymaiaadshaaeaacaaIYaaaaaGccaGLOaGaayzk
aaGaey4kaSYaaSaaaeaacaaIXaaabaGaaGOmaaaacaWGTbWaaSbaaS
qaaiaaikdaaeqaaOWaaeWaaeaacaWGwbWaa0baaSqaaiaaikdacaWG
UbaabaGaaGOmaaaakiabgUcaRiaadAfadaqhaaWcbaGaaGOmaiaads
haaeaacaaIYaaaaaGccaGLOaGaayzkaaaaaa@719F@
この等式はその変形の傾向に一致する2つのボールの回復能力を示唆します。
この条件はエネルギー損失のない弾性衝撃の1つに等しくなります。系のエネルギーの維持は次のように与えられます:
(4)
(
V
2
n
'
−
V
1
n
'
)
=
−
(
V
2
n
−
V
1
n
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aadaqadaqaaiaadAfadaqhaaWcbaGaaGOmaiaad6gaaeaacaGGNaaa
aOGaeyOeI0IaamOvamaaDaaaleaacaaIXaGaamOBaaqaaiaacEcaaa
aakiaawIcacaGLPaaacqGH9aqpcqGHsisldaqadaqaaiaadAfadaWg
aaWcbaGaaGOmaiaad6gaaeqaaOGaeyOeI0IaamOvamaaBaaaleaaca
aIXaGaamOBaaqabaaakiaawIcacaGLPaaaaaa@4C0C@
この関係は、相対速度の法線方向成分は弾性衝撃の間に、その逆に変化することを意味しています(反発係数値は単位の値に等しいため)。
法線方向成分に対して以下の式がチェックされる必要があります:
(5)
V
2
n
'
=
V
1
n
'
=
−
(
V
2
n
−
V
1
n
)
m
2
V
2
n
'
+
m
1
V
1
n
'
=
m
2
V
2
n
+
m
1
V
1
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaakq
aabeqaaiaadAfadaqhaaWcbaGaaGOmaiaad6gaaeaacaGGNaaaaOGa
eyypa0JaamOvamaaDaaaleaacaaIXaGaamOBaaqaaiaacEcaaaGccq
GH9aqpcqGHsisldaqadaqaaiaadAfadaWgaaWcbaGaaGOmaiaad6ga
aeqaaOGaeyOeI0IaamOvamaaBaaaleaacaaIXaGaamOBaaqabaaaki
aawIcacaGLPaaaaeaacaWGTbWaaSbaaSqaaiaaikdaaeqaaOGaamOv
amaaDaaaleaacaaIYaGaamOBaaqaaiaacEcaaaGccqGHRaWkcaWGTb
WaaSbaaSqaaiaaigdaaeqaaOGaamOvamaaDaaaleaacaaIXaGaamOB
aaqaaiaacEcaaaGccqGH9aqpcaWGTbWaaSbaaSqaaiaaikdaaeqaaO
GaamOvamaaBaaaleaacaaIYaGaamOBaaqabaGccqGHRaWkcaWGTbWa
aSbaaSqaaiaaigdaaeqaaOGaamOvamaaBaaaleaacaaIXaGaamOBaa
qabaaaaaa@6147@
V'
1 とV'
2 を未知量として用いる系の方程式は、簡単に解くことができます:
(6)
V
2
n
'
=
(
m
2
−
m
1
m
2
+
m
1
)
V
2
n
+
(
2
m
1
m
1
+
m
2
)
V
1
n
V
1
n
'
=
(
m
1
−
m
2
m
1
+
m
2
)
V
1
n
+
(
2
m
2
m
1
+
m
2
)
V
2
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaakq
aabeqaaiaadAfadaqhaaWcbaGaaGOmaiaad6gaaeaacaGGNaaaaOGa
eyypa0ZaaeWaaeaadaWcaaqaaiaad2gadaWgaaWcbaGaaGOmaaqaba
GccqGHsislcaWGTbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaamyBamaa
BaaaleaacaaIYaaabeaakiabgUcaRiaad2gadaWgaaWcbaGaaGymaa
qabaaaaaGccaGLOaGaayzkaaGaamOvamaaBaaaleaacaaIYaGaamOB
aaqabaGccqGHRaWkdaqadaqaamaalaaabaGaaGOmaiaad2gadaWgaa
WcbaGaaGymaaqabaaakeaacaWGTbWaaSbaaSqaaiaaigdaaeqaaOGa
ey4kaSIaamyBamaaBaaaleaacaaIYaaabeaaaaaakiaawIcacaGLPa
aacaWGwbWaaSbaaSqaaiaaigdacaWGUbaabeaaaOqaaiaadAfadaqh
aaWcbaGaaGymaiaad6gaaeaacaGGNaaaaOGaeyypa0ZaaeWaaeaada
Wcaaqaaiaad2gadaWgaaWcbaGaaGymaaqabaGccqGHsislcaWGTbWa
aSbaaSqaaiaaikdaaeqaaaGcbaGaamyBamaaBaaaleaacaaIXaaabe
aakiabgUcaRiaad2gadaWgaaWcbaGaaGOmaaqabaaaaaGccaGLOaGa
ayzkaaGaamOvamaaBaaaleaacaaIXaGaamOBaaqabaGccqGHRaWkda
qadaqaamaalaaabaGaaGOmaiaad2gadaWgaaWcbaGaaGOmaaqabaaa
keaacaWGTbWaaSbaaSqaaiaaigdaaeqaaOGaey4kaSIaamyBamaaBa
aaleaacaaIYaaabeaaaaaakiaawIcacaGLPaaacaWGwbWaaSbaaSqa
aiaaikdacaWGUbaabeaaaaaa@7628@
これらの関係は質量の比に依存することにご留意ください。
ボールはt方向については速度変化に悩まされることはないので、それぞれの球の速度の接線成分は維持され、以下が得られます:
(7)
V
1
t
'
=
V
1
t
=
V
1
cos
θ
1
V
2
t
'
=
V
2
t
=
V
2
cos
θ
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaakq
aabeqaaiaadAfadaqhaaWcbaGaaGymaiaadshaaeaacaGGNaaaaOGa
eyypa0JaamOvamaaBaaaleaacaaIXaGaamiDaaqabaGccqGH9aqpca
WGwbWaaSbaaSqaaiaaigdaaeqaaOGaci4yaiaac+gacaGGZbGaeqiU
de3aaSbaaSqaaiaaigdaaeqaaaGcbaGaamOvamaaDaaaleaacaaIYa
GaamiDaaqaaiaacEcaaaGccqGH9aqpcaWGwbWaaSbaaSqaaiaaikda
caWG0baabeaakiabg2da9iaadAfadaWgaaWcbaGaaGOmaaqabaGcci
GGJbGaai4BaiaacohacqaH4oqCdaWgaaWcbaGaaGOmaaqabaaaaaa@57E8@
衝撃の後の速度のノルムはその結果以下の関係式となります。
(8)
V
1
'
=
(
(
V
1
n
'
)
2
+
(
V
1
t
'
)
2
)
1
/
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbWaa0baaSqaaiaaigdaaeaacaGGNaaaaOGaeyypa0ZaaeWa
aeaadaqadaqaaiaadAfadaqhaaWcbaGaaGymaiaad6gaaeaacaGGNa
aaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaey4kaSYa
aeWaaeaacaWGwbWaa0baaSqaaiaaigdacaWG0baabaGaai4jaaaaaO
GaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOGaayjkaiaawMca
amaaCaaaleqabaGaaGymaiaac+cacaaIYaaaaaaa@4CEB@
(9)
V
2
'
=
(
(
V
2
n
'
)
2
+
(
V
2
t
'
)
2
)
1
/
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbWaa0baaSqaaiaaikdaaeaacaGGNaaaaOGaeyypa0ZaaeWa
aeaadaqadaqaaiaadAfadaqhaaWcbaGaaGOmaiaad6gaaeaacaGGNa
aaaaGccaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaOGaey4kaSYa
aeWaaeaacaWGwbWaa0baaSqaaiaaikdacaWG0baabaGaai4jaaaaaO
GaayjkaiaawMcaamaaCaaaleqabaGaaGOmaaaaaOGaayjkaiaawMca
amaaCaaaleqabaGaaGymaiaac+cacaaIYaaaaaaa@4CEE@
この例題では、ホールは同じ質量を持ち: m1 = m2
したがって、
V
2
'
=
V
1
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbWaa0baaSqaaiaaikdaaeaacaGGNaaaaOGaeyypa0JaamOv
amaaBaaaleaacaaIXaGaamOBaaqabaaaaa@3F0B@
V
1
n
'
=
V
2
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbWaa0baaSqaaiaaigdacaWGUbaabaGaai4jaaaakiabg2da
9iaadAfadaWgaaWcbaGaaGOmaiaad6gaaeqaaaaa@3FFE@
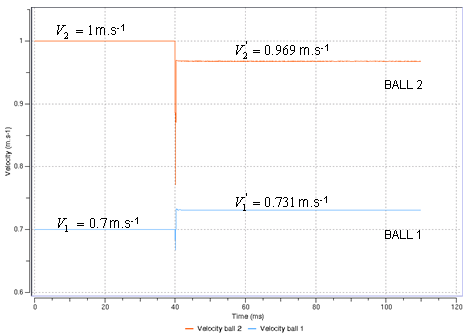
速度のノルムは以下の関係を用いて与えられ、初速度と角度に依存します。解析解を決めるために用いられます(衝突後の角度と速度):
(10)
V
1
'
=
(
(
V
2
)
2
sin
2
θ
2
+
(
V
1
)
cos
2
θ
1
)
1
/
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbWaa0baaSqaaiaaigdaaeaacaGGNaaaaOGaeyypa0ZaaeWa
aeaadaqadaqaaiaadAfadaWgaaWcbaGaaGOmaaqabaaakiaawIcaca
GLPaaadaahaaWcbeqaaiaaikdaaaGcciGGZbGaaiyAaiaac6gadaah
aaWcbeqaaiaaikdaaaGccqaH4oqCdaWgaaWcbaGaaGOmaaqabaGccq
GHRaWkdaqadaqaaiaadAfadaWgaaWcbaGaaGymaaqabaaakiaawIca
caGLPaaaciGGJbGaai4BaiaacohadaahaaWcbeqaaiaaikdaaaGccq
aH4oqCdaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaadaahaaWc
beqaaiaaigdacaGGVaGaaGOmaaaaaaa@5595@
(11)
V
2
'
=
(
(
V
1
)
2
sin
2
θ
1
+
(
V
2
)
cos
2
θ
2
)
1
/
2
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacaWGwbWaa0baaSqaaiaaikdaaeaacaGGNaaaaOGaeyypa0ZaaeWa
aeaadaqadaqaaiaadAfadaWgaaWcbaGaaGymaaqabaaakiaawIcaca
GLPaaadaahaaWcbeqaaiaaikdaaaGcciGGZbGaaiyAaiaac6gadaah
aaWcbeqaaiaaikdaaaGccqaH4oqCdaWgaaWcbaGaaGymaaqabaGccq
GHRaWkdaqadaqaaiaadAfadaWgaaWcbaGaaGOmaaqabaaakiaawIca
caGLPaaaciGGJbGaai4BaiaacohadaahaaWcbeqaaiaaikdaaaGccq
aH4oqCdaWgaaWcbaGaaGOmaaqabaaakiaawIcacaGLPaaadaahaaWc
beqaaiaaigdacaGGVaGaaGOmaaaaaaa@5596@
速度の投影を記録することにより、衝撃後の方向は関係式(9)を用いて評価できます。解析解を決めるために用いられます(衝突後の角度と速度):
(12)
θ
1
'
=
arcsin
(
V
2
V
1
sin
θ
2
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqaH4oqCdaqhaaWcbaGaaGymaaqaaiaacEcaaaGccqGH9aqpciGG
HbGaaiOCaiaacogacaGGZbGaaiyAaiaac6gadaqadaqaamaalaaaba
GaamOvamaaBaaaleaacaaIYaaabeaaaOqaaiaadAfadaWgaaWcbaGa
aGymaaqabaaaaOGaci4CaiaacMgacaGGUbGaeqiUde3aaSbaaSqaai
aaikdaaeqaaaGccaGLOaGaayzkaaaaaa@4D7C@
(13)
θ
2
'
=
arcsin
(
V
1
V
2
sin
θ
1
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbwvMCKf
MBHbqefqvATv2CG4uz3bIuV1wyUbqedmvETj2BSbqefm0B1jxALjhi
ov2DaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY=Hhbbf9v8
qqaqFr0xc9pk0xbba9q8WqFfea0=yr0RYxir=Jbba9q8aq0=yq=He9
q8qqQ8frFve9Fve9Ff0dmeaacaGacmGadaWaaiqacaabaiaafaaake
aacqaH4oqCdaqhaaWcbaGaaGOmaaqaaiaacEcaaaGccqGH9aqpciGG
HbGaaiOCaiaacogacaGGZbGaaiyAaiaac6gadaqadaqaamaalaaaba
GaamOvamaaBaaaleaacaaIXaaabeaaaOqaaiaadAfadaWgaaWcbaGa
aGOmaaqabaaaaOGaci4CaiaacMgacaGGUbGaeqiUde3aaSbaaSqaai
aaigdaaeqaaaGccaGLOaGaayzkaaaaaa@4D7C@