RD-E:0901 ビリヤード(プール)
プールゲームがモデル化され、1個のボールが15個のボールに衝突する間の運動量の伝達が示されます。
この例題の目的は、複数のボール間の運動量の伝達について調査することにあります。ペナルティ法とLagrange乗数法を用いた様々なインターフェースでの接触が解析されます。
使用されるオプションとキーワード
- 16節点厚肉シェルと球形メッシュ(/PROP/TYPE20 (TSHELL))
- Lagrange乗数法とペナルティ法を用いたTYPE7インターフェース(/INTER/TYPE7)
- TYPE16スライディングとライドインタオーフェース、2次曲面接触(/INTER/LAGMUL/TYPE16)
- 弾性衝撃
- 運動量伝達と衝撃波
- 初速度(/INIVEL)
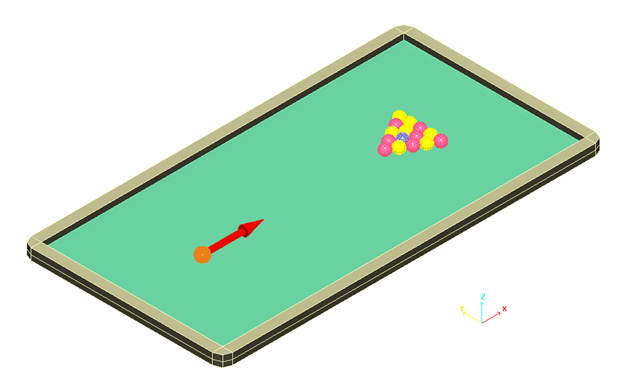
図 1. 衝突するボールの初期並進速度
テーブルの下側の面の全ての節点は完全に拘束されます(並進と回転)。
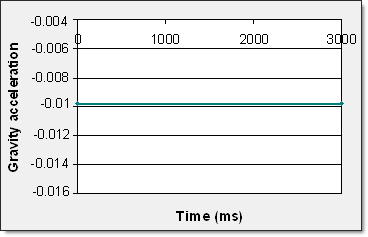
図 2. 重力関数(-0.00981 mm.ms-2)
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
本例題で使用されるモデルファイルは下記のとおり:
BILLIARD_*.rad
モデル概要
図 3. プールゲーム
単位: mm、g、N、MPa。
- 材料プロパティ:ボール(フェノール樹脂)
- 初期密度
- 0.00137 g.mm-3
- ヤング率
- 10500
- ポアソン比
- 0.3
- 材料プロパティ:フレーム(ポリマー)
- 初期密度
- 0.001 g.mm-3
- ヤング率
- 1000
- ポアソン比
- 0.49
- 材料プロパティ:板(スレート)
- 初期密度
- 0.0028 g.mm-3
- ヤング率
- 62000
- ポアソン比
- 0
モデリング手法

図 4. プールゲームメッシュ
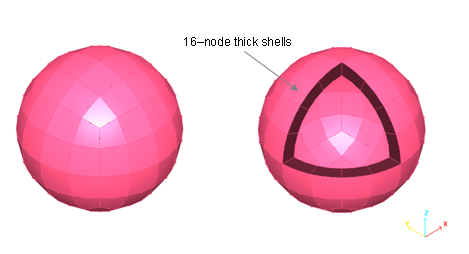
図 5. ボールのメッシュ
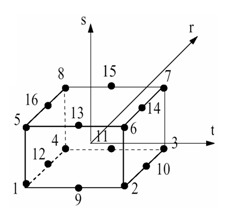
図 6. 16節点厚肉シェル要素
図 7. TYPE16インターフェース: セカンダリのSHEL16がボールでメインのSHEL16がテーブル

図 8. ボール間の接触のために定義されるTYPE16インターフェースの例
セカンダリ節点(赤)はパートのサーフェスから取り出されます。
結果
曲線とアニメーション

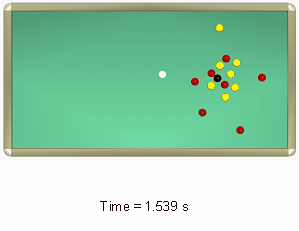
図 9.
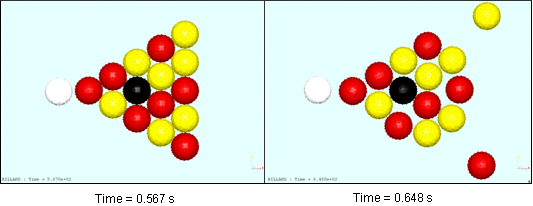
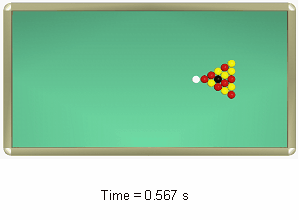
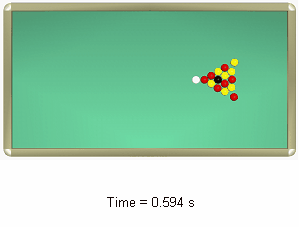
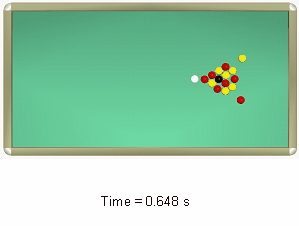
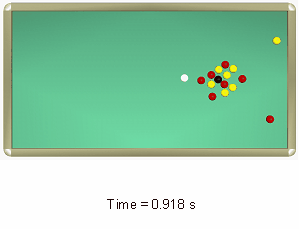
図 10. ボールの衝突
 |
 |
 |
 |
 |
 |