トポロジー最適化 - 製造可能性
トポロジー最適化での懸念は、開発された設計概念が製造可能なものにならないことがよくあるという点です。もう1つの問題は、適切な手段を取らない場合、トポロジー最適化の問題の解がメッシュ依存になることがあるという点です。
OptiStructでは、トポロジー最適化を行う際に製造可能性を扱う方法が以下のようにいくつか用意されています。
部材寸法制御
最終的なトポロジーでの部材寸法および最終設計の簡潔さの度合いを制御できます。
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DOPTPR | MINDIM | VALUE |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) |
|---|---|---|---|---|---|---|---|---|---|
| DTPL | ID | PTYPE | PID1 | PID2 | PID3 | PID4 | PID5 | PID6 | |
| PID7 | 同様 | 同様 | 同様 | ||||||
| MEMBSIZ | MINDIM | MAXDIM | MINGAP |
ここでは、部材の望ましい最小直径MINDIM、および最大直径MAXDIMの両方を、MEMBSIZ継続行で定義できます。このようにして、DTPLごとに異なる部材寸法を定義できます。MINGAPは、形成される構造部材間の最小間隔を定義します。これは、MAXDIMと併せてのみ使用されます。MAXDIMの使用は、MAXDIMと同じ値のMINGAP制約が適用されることを意味します。したがって、MINGAPが効果を持つためには、MAXDIMよりも大きい値にする必要があります。
最小部材寸法制御
最小部材寸法制御では小さな部材の形成にペナルティが科されますが、それでもなお、指定の最小部材寸法より著しく小さい部材を含む結果が得られる場合があります。
これは、その構造では小さな部材が荷重の伝達で非常に重要となる可能性があり、ペナルティを科しても削除されないためです。最小部材寸法制御は、量の制御より質の制御として機能します。
離散解は2つの反復ステップで得られます。最初のステップでは、中間密度の要素を多く含む解に収束します。次のステップでは、この解を密度が1である部材の解に改善します。それぞれのステップが、何回も反復されます。最初のステップは、2度の全収束フェーズで構成されます。最初は初期離散値(DOPTPRMバルクデータエントリ上のDISCRETEおよびDISCRT1Dパラメータにより定義)で実行され、次に、離散値を1.0増やして実行されます。この手順は、明確に定義された部材による解を得るためのものです。明確に定義された部材による解をこのステップで生成できなかった場合、望ましい最小部材寸法は2番目のステップには保持されません。この場合は、離散パラメータを大きくするか、収束トレランス(DOPTPRMバルクデータエントリのOBJTOLパラメータにより定義)を小さくするか、またはその両方の措置をとり、最初のフェーズの解を改善する必要があります。デフォルトの離散パラメータは、1次元要素、プレートおよびシェルに対しては1.0に、3次元ソリッドに対しては2.0に設定されています。
一般に、MINDIMがアクティブになると、チェッカーボード処理はこの機能に適用された方法により制御され、CHECKERパラメータは不要となります。まれに、上記の2度目のフェーズでも、3次元ソリッドに対してチェッカーボードが導入される場合があります。この場合には、MMCHECKパラメータにより、追加のチェッカーボード制御アルゴリズムをアクティブにできます(CHECKERパラメータおよびMMCHECKパラメータは、DOPTPRMバルクデータエントリを使用して定義します)。
このカードを使用することによって、チェッカーボードが使用されない解を得ることができます。ただし、CHECKER=1と設定した場合のように、中間密度の要素を多く含む解に達するという望ましくない副次的な影響があります。したがって、このカードは必要な場合にのみ使用してください。
MINDIMは、DTPLから参照するすべての要素(DOPTPRMで要素を定義している場合は、設計可能なすべての要素)の平均要素寸法の少なくとも3倍以上かつ12倍以下とすることをお奨めします。2次元要素の平均要素寸法は、要素の面積の平方根の平均として計算され、3次元要素の平均要素寸法は、要素の体積の立方根の平均として計算されます。
この推奨事項は、他の製造用制約条件と組み合わされる場合が対象となります。定義されたMINDIMがこの値より小さい場合、平均要素寸法の3倍に等しいデフォルトの値にリセットされます。同様に、定義されたMINDIMが平均要素寸法の12倍より大きい場合、平均要素寸法の12倍に等しい値にリセットされます。この制限は、MINDIMの制約を満足させるために必要な非常に多くの要素数を追跡しなければならないために、大きくなり過ぎ得るメモリ使用量を削減するために設定されています。メッシュが型抜き方向または押し出し方向に合わせて並んでいる構造では、DTPLカードのMESH継続行にMTYPをALIGNとして設定することで、この制約条件は適用されなくなります。
- Michellトラスの例
- MBB梁の例
- アーチの例
- 3次元橋梁モデルの例
最大部材寸法制御
大きな部材の形成にペナルティを科します。この制御では、部材の寸法の方向は考慮されません。つまり、部材の厚みがいずれかの方向でMAXDIMより薄ければ、この制約条件は満足されたことになります。これは、鋳造部品に設けるリブの厚みを制御する際の要求に一致します。
MAXDIMは、MINDIMの2倍以上とする必要があります。したがって、該当のDTPLから参照する要素すべての平均要素寸法の6倍以上の値をMAXDIMに設定することが、最小限のメッシュ要件となります。この制約条件の強制力は強く、この基準が満たされない場合はエラーが発生して処理が終了します。さらに、MAXDIMは、設計領域で最も薄い部分の幅の半分未満の値とする必要があります。
上記の制約条件によれば、この製造用制約条件でよい結果を得るには、細かいメッシュが必要となります。
最大部材寸法制御を使用すると、実現可能な設計領域に対する制限が増えるので、本当に必要な場合にのみ使用するようにします。また、この機能は新たに研究開発されたものであり、改善の途上にあります。適用例によっては、最終的な解に多くの中間密度が含まれるという副次的な効果が見られます。したがって、技術的に確立されるまで、この機能の使用には慎重を期すことをお奨めします。
MAXDIMもまた同じ寸法の部材の配置を強制しますが、体積率として評価した場合、最大で0.5までです。構造の応答について制約を含む問題では、これは制約条件を満たす妨げとなる場合があります。MAXDIMの使用に利点があるか、また、ターゲットの体積が適用可能かどうかを確認するためにまず、MAXDIMなしで設計問題の挙動を十分検討することを強く推奨します。
次の例では、最大部材寸法制御が設計結果に及ぼす影響を示しています。
例:エンジンブラケット

図 1. 型抜き方向制約条件のあるエンジンブラケット設計

図 2. 型抜き方向制約条件および最大部材寸法制約条件のあるエンジンブラケット設計
例:ハンドルブラケット
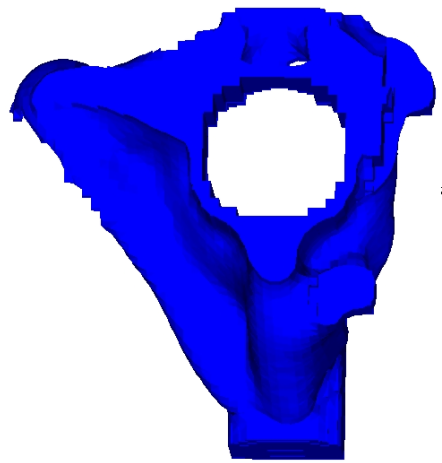
図 3. 型抜き方向制約条件のあるハンドルブラケット設計

図 4. 型抜き方向制約条件および最大部材寸法制約条件のあるハンドルブラケット設計
型抜き方向制約条件
鋳造プロセスでは、ダイのスライド方向に開かずに並んでいる空洞状の形状というものは実現不可能です。トポロジー最適化により得られた設計には、しばしば、鋳造不能な空洞が発生します。
このような設計案を製造可能な設計に変換するのは、不可能ではなくても、非常に困難です。この変換が行われる場合、設計の最適性に甚大な影響を与える可能性が高くなることもあります。
OptiStructでは、得られたトポロジーでダイが指定の方向にスライドできるよう、型抜き方向制約条件を設定できます。これらの制約条件は、DTPLカードを用いて定義されます。PSOLID IDで指定した構造部分ごとに、異なる制約条件を適用できます。2つのDRAWオプションが使用可能です。オプションSINGLEでは、1つのダイを使用し、指定の型抜き方向にスライドするものとします。対象となる鋳造部品の底面は、ダイと一対一で対応するように事前定義された部分です。オプションSPLITは、与えられた型抜き方向に分割した2つのダイを使用して、このDTPLカードで指定されたパートを鋳造することを前提とします。2つのダイの分割面を、最適化プロセスで最適化します。
一部の設計では、貫通穴が存在しないことがしばしば1つの要件となります。このような穴は、NO HOLEオプションの使用によって、型抜きの方向に形成されることを阻止できます。このパラメータはDTPLカードで定義されます。NO HOLEオプションを使うと、トポロジーは境界から一度に1つの層ずつだけ徐々に展開することができ、場合によっては1つの層を削除するのに数度の繰り返し計算を要することもあります。
SINGLE型抜きオプションで使用可能なのが、成形またはシートメタル製造可能性です。このオプションは、3次元設計領域からの3次元シェルとして解釈可能な結果を出力します。これにより、2次元シェルまたは成形されたパートの3次元設計領域からの設計が可能となり、設計にさらなる柔軟性が与えられます。STAMPオプションも、結果のシェルまたは成形されたパートの希望する板厚を表す板厚値と共に、DTPLカードで指定されます。
鋳造には、設計可能領域のほかに、非設計領域を含むこともできます。これらの非設計領域は、部品を記述したDTPLカード上で、鋳造プロセスの障害物として定義する必要があります。これにより、最終的な構造で鋳造可能性を維持できます。
また、型抜き方向制約条件の下で使用するデフォルトの最小部材寸法が存在します。これは、内部的に、関連するコンポーネントの平均メッシュ寸法の3倍と決められます。したがって、デフォルトの最小寸法の部材を十分に満たすことができる材料が得られるように、モデルのメッシュ密度と目標の体積率を選択する必要があります。DTPLカードで定義した設計部分ごとに、希望の最小部材寸法を指定できます。この値は、デフォルト値より大きくする必要があります。デフォルト値以下に設定すると、デフォルト値に置き換えられます。
例:ねじりを受ける梁
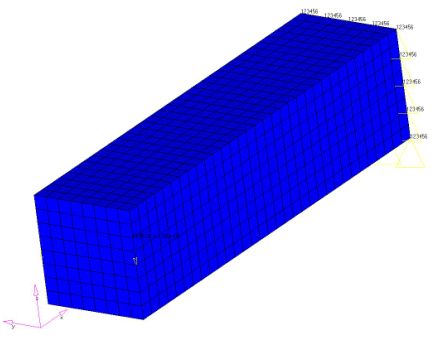
図 5. ねじりを受けているビームの有限要素モデル
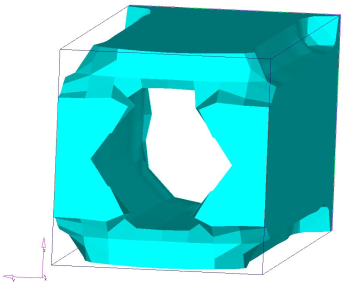
図 6. 型抜き方向について製造用制約条件のない設計
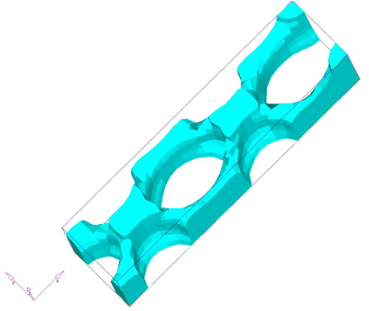
図 7. 型抜き方向がZ軸方向で、ダイオプションがSINGLEの設計
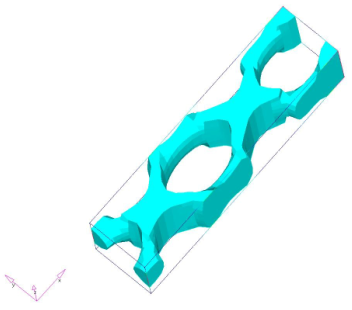
図 8. 型抜き方向がZ軸方向で、ダイオプションがSPLITの設計
予想通り、製造用制約条件がない場合の結果は、ねじり荷重に対する最適トポロジーであるチューブ状の構造となります。ただし、この設計では、Z軸方向にダイをスライドできません。鋳造においてダイのスライドを可能とした結果は、わかりやすいものではありません。この結果では、ねじり荷重が固定端に達するまで、ねじり荷重と交差する周期的なパターンをX軸方向に形成します。交差する点に材料が非常に多いのは、この点でせん断力が2倍になることを反映しているためです。上向きのCチャネルの解と比較すると、この交差パターンではすべてのXセルで応力が周期的にかかるため、システムレベルの曲げ作用を持つ解に対して、ビームの長さが及ぼす影響を排除できるという利点があります。
例:エンジンブラケット
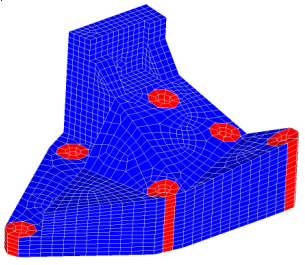
図 9. ブラケットの有限要素モデル
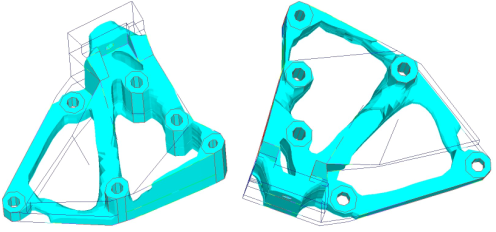
図 10. 型抜き方向がZ軸方向で、ダイオプションがSINGLEの設計
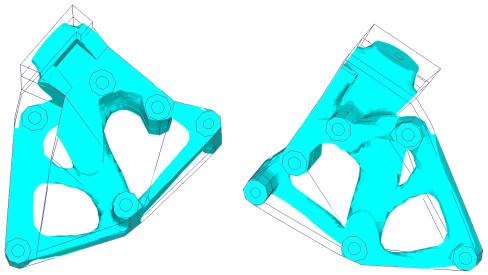
図 11. 型抜き方向がZ軸方向で、ダイオプションがSPLITの設計
例:コンプレッサのマウンティングブラケット
この例では、コンプレッサのマウンティングブラケットにトポロジー最適化を実行し、NO HOLE製造性制約条件の効果が示されます。有限要素モデルを図 12に示します。赤で示されている領域は非設計空間、青は設計空間を示します。操作条件を表す4つの異なる荷重条件が考慮され、モデルは約90,000の要素で構築されています。設計問題は、設計の体積率を制約条件とし、コンプライアンスを目的関数として最小化するよう定式化されました。
図 13 は、NO HOLE製造制約条件使用なしのコンプレッサのマウンティングブラケットの設計案を示しています。図から分かるとおり、設計には貫通穴が含まれています。

図 12. コンプレッサのマウンティングブラケットの設計領域と非線形領域を表す有限要素モデル
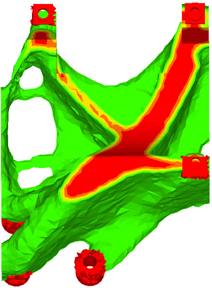
図 13. NO HOLEオプションを使用しない設計案
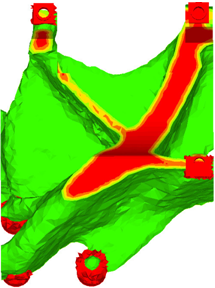
図 14. NO HOLEオプションを使用した設計案
例:自動車のブラケット
この例のブラケットは、NO HOLE制約条件とSTAMP制約条件を組み合わせて設計されたものです。スタディの目的は、貫通穴を有さない設計案を構築し、同時にシートメタル設計として解釈可能とすることです。ここではSTAMP制約条件は、シートメタル設計を表す3次元シェル解釈可能構造の形成を強制します。4つの異なる荷重条件を表す4つのサブケースが考慮され、モデルは約20,000要素で構成されています。最適化問題は、制約されている設計体積率について重み付きのコンプライアンス(サブケース毎に1つのコンプライアンス値)を最小限にするよう定式化されます。これにより、指定された材料の分量に対して最もスティフな設計が展開されます。
図 15 は、ブラケットの設計空間および非設計空間の有限要素モデルを表しています。赤で示される領域は非設計空間、青は設計空間です。
図 16 は、STAMPおよびNO HOLE製造要件を考慮しない設計提案です。そのような設計を鋳造するのは可能ですが、そのようなパートを成形することは実現不可能です。
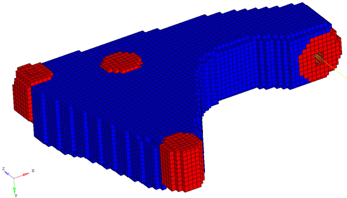
図 15. ブラケットの設計領域と非線形領域を表す有限要素モデル
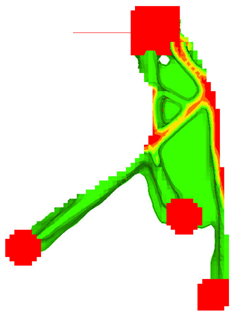
図 16. 'STAMP'および'NO HOLE'を使用しない設計案
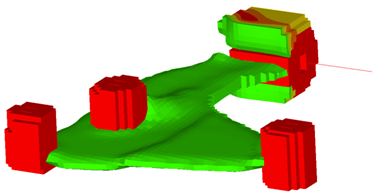
図 17. 'STAMP'および'NO HOLE'を使用した設計案(view 1)
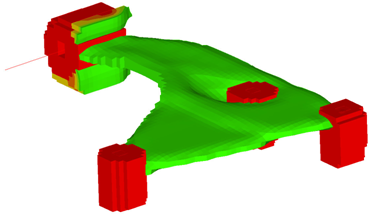
図 18. 'STAMP'および'NO HOLE'を使用した設計案(view 2)
押し出し制約条件
トポロジー最適化で押し出しの製造用制約条件を適用することにより、初期メッシュ、境界条件、荷重に関係なく、一定の断面を持つソリッドモデルの設計が可能です。
指定したパスに沿って一定の断面を持つような設計を生成することが必要な場合があります。特に、押し出しプロセスで製造する部品がこの状況に該当します。
押し出し制約条件は、特に押し出し手順を使用して製造する必要のない、構造の概念設計スタディにも使用できます。これらの要件は、特定の形状制約条件と見なすことができ、このような特徴が必要なあらゆる設計で使用できます。たとえば、リブがソリッド領域の深さ全体に及ぶような構造にすることが必要な場合があります。
他の製造性制約条件のように、押し出し制約条件もコンポーネントレベルで適用でき、DTPLカードを使用して、最小部材寸法制御と同時に定義できます。
問題の設定

図 19. ねじれのない断面とねじれのある断面
押し出しパスの定義

図 20. 押し出しパスを定義するための4節点
上の例で、押し出しパスを定義するために4つの節点が使用されています(左図)。ここで、OptiStructで計算されたこのパスは不正確です。さらに正確に近似するには、押し出しパスにもっと多くの節点を使用します(右図)。
ねじれのある断面では、上記と同じ手順により、EPATH2フィールドで2次押し出しバスを定義する必要があります。
例:湾曲した梁
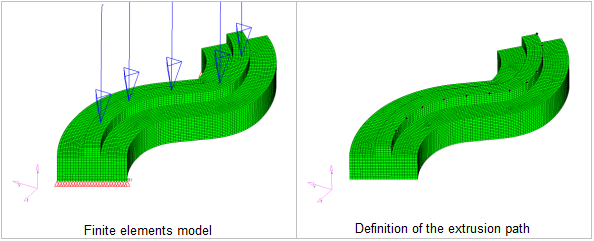
図 21. 湾曲した梁
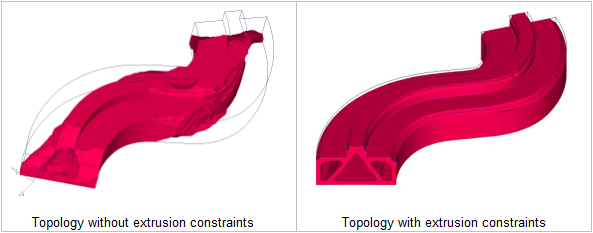
図 22. 押し出し制約条件
例:階段形状の構造
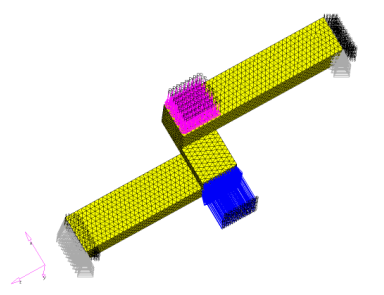
図 23. 階段形状の構造
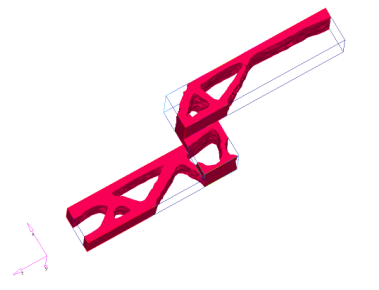
図 24. 結果の剛性パネル
例:押し出し制約条件
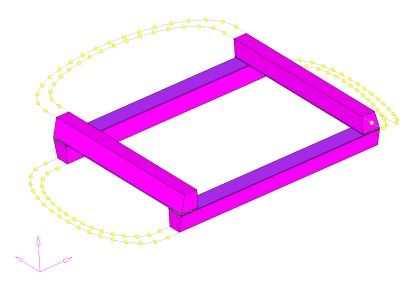
図 25.
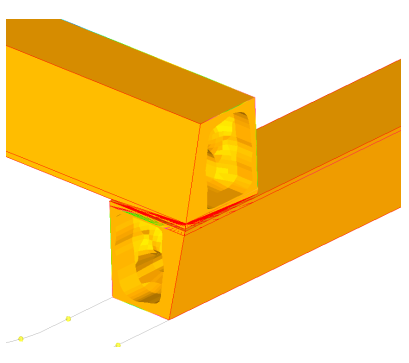
図 26. 非連続ソリッドメッシュ
パターン繰り返し
相似のトポロジーの配置を生成するために、異なる構造のコンポーネントをリンクできるようにする技法。
この目的を達成するには、メイン(旧称“マスター”)DTPLカードを定義し、このメインを参照する任意の数のセカンダリ(旧称“スレーブ”)DTPLカードを定義する必要があります。メインコンポーネントとセカンダリコンポーネントは、局所座標系(必須)およびスケーリング係数(オプション)で互いに関連付けられます。
最小部材寸法または最大部材寸法、型抜き方向制約条件、押し出し制約条件などの製造用制約条件は、meinn DTPLカードに適用します。これにより、これらの制約条件は自動的にセカンダリDTPL カードに適用されます。
- メインDTPLカードを作成します。
- その他の製造用制約条件を必要に応じて適用します。
- メインDTPLカードに関連付けられた局所座標系を定義します。
- セカンダリDTPLカードを作成します。
- セカンダリDTPLカードに関連付けられるた局所座標系を定義します。
- 必要に応じてスケーリング係数を適用します。
- 任意の数のセカンダリDTPLカードについて、手順4~6を繰り返します。
局所座標系
- CAID
- 局所座標系のアンカーポイントを定義します。
- CFID
- X軸の方向を定義します。
- CSID
- XY平面を定義し、Y軸の正方向を指定します。
- CTID
- Z軸の正方向を指定します。

図 27. 右手座標系と左手座標系
スケーリング係数

図 28.
型抜き方向制約条件のあるパターン繰り返し
型抜き方向制約条件を、パターン繰り返しと同時に適用できます。このためには、メインDTPL カードで型抜き方向を定義します。これにより、セカンダリの型抜き方向は局所座標系に基づいて自動的に生成されます。
本来は同一ではないコンポーネントがある場合でも、それぞれのコンポーネントの最適化された設計は、型抜き方向制約条件を満たします。特に、異なるコンポーネントに異なる障害物が含まれる場合には、すべての障害物の組み合わせが必ず考慮されます。
押し出し制約条件のあるパターン繰り返し
押し出し制約条件も、パターン繰り返しと併せて使用できます。これにより、同一断面を持つ部品を生成できます。コンポーネントは3方向に同一である必要はなく、部品ごとに独自の押し出しパスを持つことができます。
各コンポーネントが異なる押し出しパスを持つ場合、これらのパスは、該当のDTPL カードごとに明示的に定義する必要があります。ただし、コンポーネントが同一の押し出しパスを持つ場合、セカンダリの押し出しパスはメインの押し出しパスに基づいて自動的に計算されます。
例:ブロックモデル
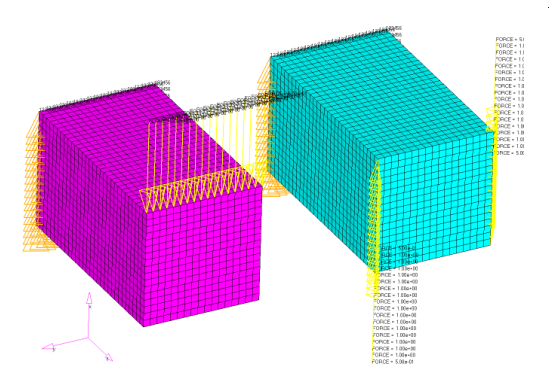
図 29. 2つの異なる方法で荷重を受ける類似したブロック
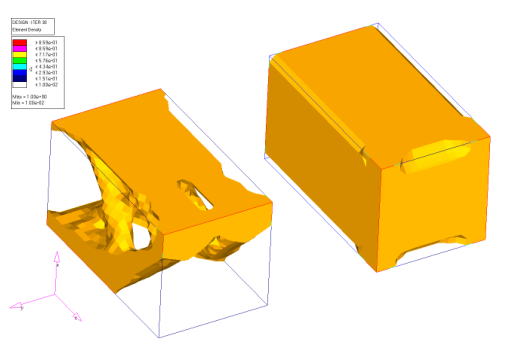
図 30. 最初の図と同じビュー
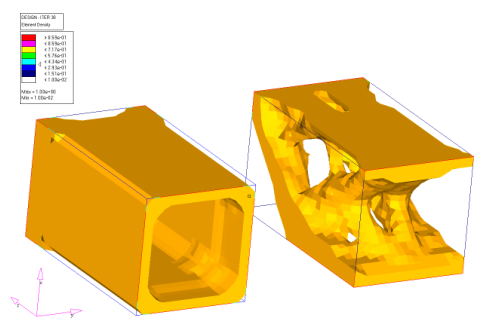
図 31. 青緑色のブロックが空洞になっていることを示す後方からのビュー

図 32.
例:簡素化した翼のモデル

図 33. 簡素化した翼のモデル
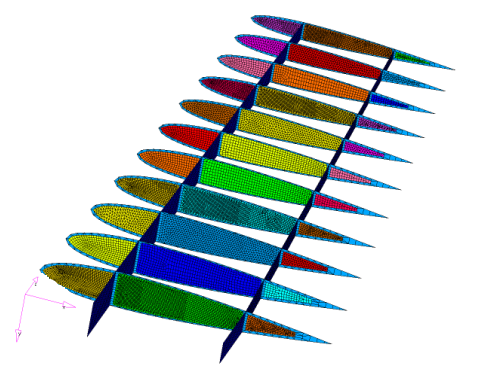
図 34.

図 35. 各領域が独立である場合の最適化されたトポロジー
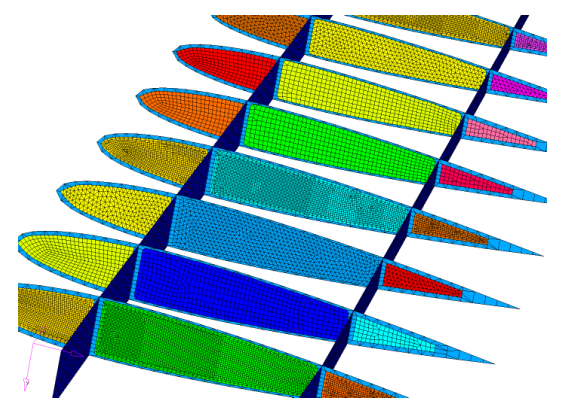
図 36.
パターングルーピング
パターングルーピングは、特定のパターンで設計することが必要なドメインの単一部分を定義できる機能です。
平面対称性
対称性のある設計を行うことが求められる場合がよくあります。設計空間および境界条件が対称的でも、従来のトポロジー最適化方法では、完全に対称な設計ができるとは限りませんでした。
トポロジー最適化に対称性制約条件を適用することにより、初期メッシュ、境界条件、荷重に関係なく、対称的な設計が可能になります。対称性は、1つの平面、2つの直交平面、または3つの直交平面に適用できます。OptiStructにより対称面全域でほぼ同じ値を持つ変数が生成されるので、対称メッシュは必要ありません。

図 39. 1平面対称性

図 40. 2平面対称性

図 41. 3平面対称性
均一な要素密度
パターングルーピングは、選択されたコンポーネント全体に均一な要素密度を要求するための可能性も提供します。
パターングループは、選択されたコンポーネントのすべての要素が互いに同じ要素密度を維持することを確実にします。
周期対称性
パターングルーピングを使用すれば、周期対称性も定義できます。
周期的パターングルーピングにより、設計が中心軸の周囲に、指定した回数だけ繰り返されます。さらに、周期的繰り返しは、それ自体が対称的となり得ます。このオプションを選択すると、OptiStructは各ウェッジをその中心線に対して対称とします。

図 42.

図 43.
型抜き制約条件
型抜き方向制約条件を、パターングルーピングと組み合わせることができます。

図 44. 1平面対称性
2平面および3平面に対する対称性、および周期対称性にも同じ考え方が適用されます。
製造可能な設計を得るためには注意が必要です。たとえば、周期対称性では、型抜き方向を対称軸に平行とする必要があります。
押し出し制約条件
現時点では、押し出し制約条件をパターングルーピングと同時に使用することはできません。
例:ソリッドブロック
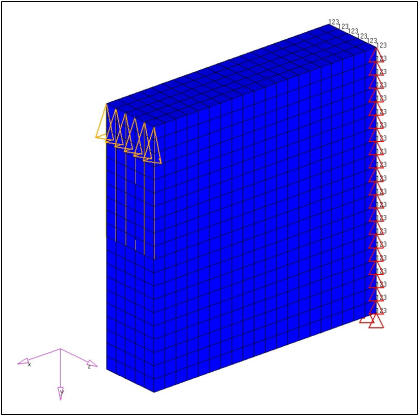
図 45. 材料のソリッドブロック
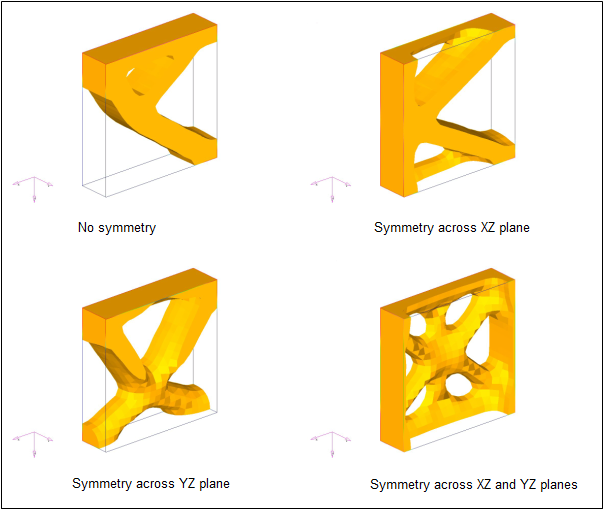
図 46. さまざまな対称性の組み合わせについて得られた結果
例:車の車輪モデル
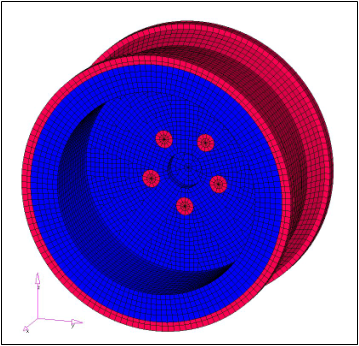
図 47. 車の車輪モデル
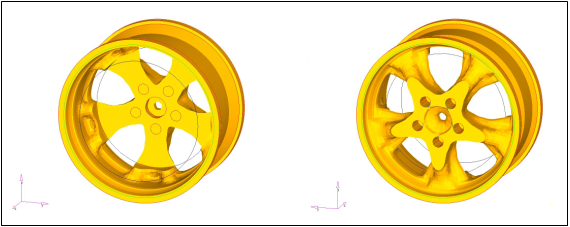
図 48.

