陽解法の例題
浅い円筒型ルーフの中央点に強制速度が与えられます。この例題では陽解法アプローチを用います。
この例題の目的は、1つの不安定性を持つスナップスルー問題を検討することにあります。したがって、構造は荷重の下で曲げられます。結果は参考文献の解と比較されます。 1
使用されるオプションとキーワード
節点時刻歴は、圧力の出力を示しません。このような出力を点Cで得るためには、この点に剛体を生成する必要があります。点Cには一定の強制速度-0.01 ms-1 がZ方向に与えられます。その変位は時間に比例します。
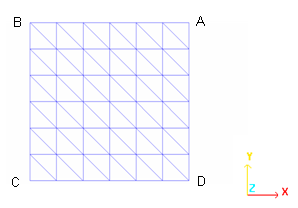
- 辺BCはX方向並進とYとZ軸周りの回転が拘束されます(対称条件)。
- 辺CDはY方向並進とXとZ軸周りの回転が拘束されます(対称条件)。
- 辺DAはX、Y、Z方向並進とXとZ軸周りの回転が拘束されます。
- 点CはX、Y方向並進と、X、Y、Z軸周りの回転が拘束されます。

図 1. 境界条件
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
本例題で使用されるモデルファイルは下記のとおり:
SNAP_EXP*.rad
モデル概要
真っ直ぐな辺がピン拘束された浅い円筒ルーフがその中央点に強制速度を受けます。
単位: mm、ms、g、N、 MPa
- l
- 254 mm
- R
- 2540 mm
- シェル厚
- t = 12.7 mm
- 0.1 rad
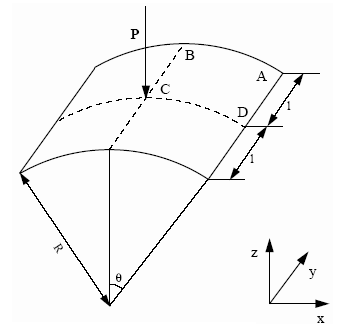
図 2. 問題の形状データ
- 材料特性
- 初期密度
- 7.85x10-3
- ヤング率
- 3102.75
- ポアソン比
- 0.3
モデリング手法
構造は完全で、欠陥はありません。対称性を考慮して、シェルの1/4のみがモデル化されます(面 ABCD)。
結果
曲線とアニメーション
対称性のため全荷重の1/4のみが与えられます。このため、時刻歴として示される剛体の力Fzは力Pを得るために4倍される必要があります。
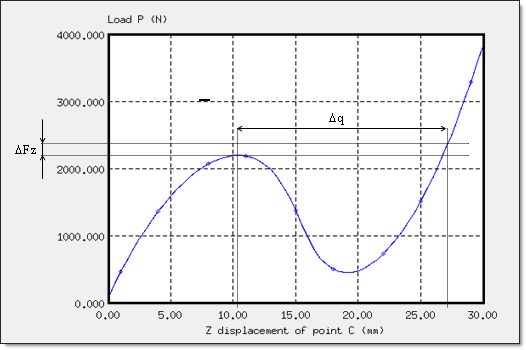
図 4. 点Cでの荷重P vs 変位: スナップスルーの不安定性
点Cの変位はその絶対値で示しています。曲線はスナップスルーの不安定性の特性を示しています。限界荷重を超えた後、シェルの崩壊のため、無限への荷重増加で大きな変位の増加を引き起こすことになります。
最初の極値が限界荷重=2208.5 N(点Cの変位 = 10.5 mm)を定義します。
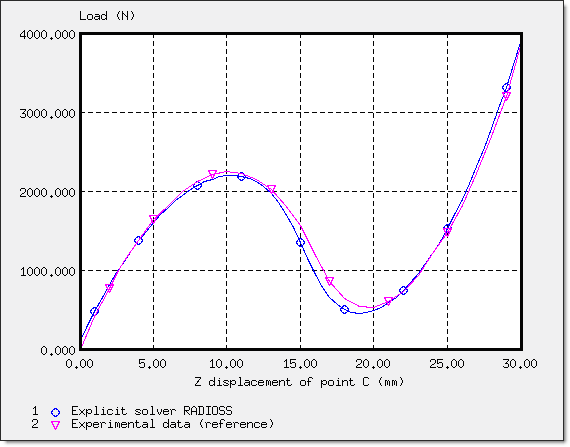
図 5. 参考文献の曲線とRadiossを用いて得られた曲線の比較
2つの曲線の違いは変位の少ない領域(5 mmまで)では約10%で、曲線の高い非線形の領域(5mmと20 mmの間)ではもう少し大きく(15%)なっています。変位が20 mmを超えた領域では、曲線はより近くなっていることが確認できます。
| 変形メッシュ(輪郭表示) – 変位ノルム |
|---|
 初期形状 |
 スナップスルーの開始 |
 大移動フェーズ |
 安定形状 |
 新しい剛な構造での載荷 |