陰解法の例題

浅い円筒ルーフがその中央点に強制速度を受けます。解析では陰解法アプローチを用います。

この例題の目的は、1つの不安定性を持つスナップスルー問題を検討することにあります。したがって、構造は荷重の下で曲げられます。結果は参照の解 と比較されます。1 孤長増分法を用いた陰解法のストラテジーが示されます。

使用されるオプションとキーワード

  • 陰解法ソルバー、弧長増分法による時間ステップコントロール
  • 非線形静解析
  • 安定性、スナップスルー、および限界荷重
  • T3シェル
  • 境界条件（/BCS）
  • 陰解法オプション（陰解法）
  • 強制速度（/IMPVEL）
  • 剛体（/RBODY）

限界点が主な非線形性を引き起こします。したがって、静的非線形解析が孤長変位のストラテジーを用いて実行されています。時間ステップが変位ノルム制御によって決められます。荷重変位曲線の0の接線で特性化される限界点を超え、非線形経路の増加と減少部分を表すため、小さな時間ステップが必要で、これは最大値の設定で保障されます。

それぞれの非線形反復サイクルでAx=b を解くソルバーの手法が必要です。これは/IMPL/SOLVERで定義されます。
線形陰解法オプション
線形ソルバー
直接法ソルバーMUMPS
前処理法
分解された近似逆行列
最大反復回数
系の次元（NDOF）
終了基準
力の相対残差
終了基準の収束判定
マシンの精度
*_001.radに設定される入力の陰解法オプションは：
/IMPL/PRINT/NONL/-1
非線形反復の出力間隔
/IMPL/SOLVER/2 5 0 0 0.0
ソルバー法（Ax=bを解く）
/IMPL/NONLIN 3 1 0.20e-3
非線形静解析の計算
/IMPL/DTINI 10
初期荷重時増分を決める初期時間ステップ
/IMPL/DT/STOP 0.5 10
時間ステップの最小と最大値
/IMPL/DT/2 6.0 20 0.8 1.05
時間ステップコントロール法 2 – 孤長増分 + ラインサーチが収束の加速と制御のために用いられます

陰解法オプションの詳細についてはRadiossStarter入力をご参照ください。

入力ファイル

必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。

本例題で使用されるモデルファイルは下記のとおり：

SNAP_IMP*.rad

モデル概要

真っ直ぐな辺がピン拘束された浅い円筒ルーフがその中央点に強制速度を受けます。

単位： mm、ms、g、N、 MPa

形状データの寸法は図 1のとおりです：
l
254 mm
R
2540 mm
シェル厚
t = 12.7 mm
θ
0.1 rad

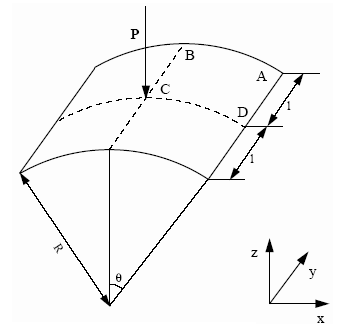
rad-ex-fig_2-6
図 1. 問題の形状データ
用いられた材料は線形弾性則に従い、以下の特性を持ちます：
材料特性
初期密度
7.85x10-3 [ g m m 3 ] MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9 vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaamWaaeaada WcaaqaaiaadEgaaeaacaWGTbGaamyBamaaCaaaleqabaGaaG4maaaa aaaakiaawUfacaGLDbaaaaa@3BBC@
ヤング率
3102.75 [ MPa ] MathType@MTEF@5@5@+= feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9 vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr 0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaadaWadaqaai Gac2eacaGGqbGaaiyyaaGaay5waiaaw2faaaaa@3BE6@
ポアソン比
0.3

モデリング手法

陽解法の検討で記述された問題のモデリングは変わっていません。

陰解法計算では特定の陰解法パラメータがEngineファイル*_001.radで/IMPLで始まるオプションを用いて定義される必要があります。

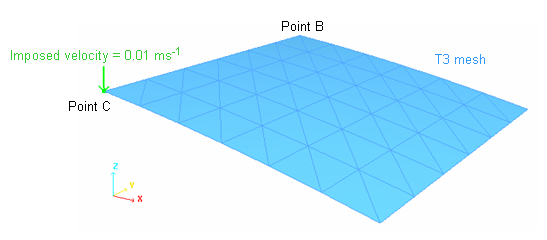
rad_ex_fig_2-7
図 2. 問題の概要（1/4のシェルがモデル化されています）
強制速度が陰解法を用いて考慮されます。ここで、一定の入力曲線が計算時間に一致する強制変位に変換されます。

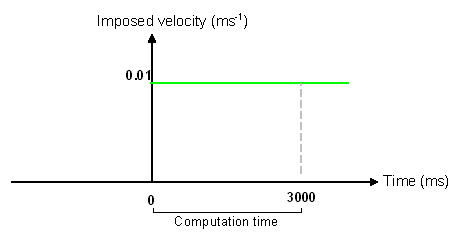
rad_ex_fig_2-8
図 3. 強制速度曲線

結果

曲線とアニメーション

対称性のため全荷重の1/4のみが与えられます。このため、時刻歴として示される剛体の力 Fzは力 Pを得るために4倍される必要があります。

図 4 はスナップスルーの荷重変位曲線の特性を表します。この図はシェルの点Cにおける反力を鉛直変位の関数としてプロットしたものです。陰解法の結果は実験データと比較されます。

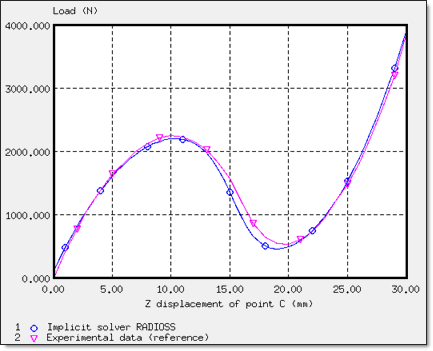
rad_ex_fig_2-9
図 4. 点Cでの荷重P vs 変位
10 ms以下の時間ステップで（最大値は陰解法/IMPL/DT/STOPオプションで設定されます）、参考文献で得られた良い結果と、Radiossとの一致が達成されます。精度は、CPU 時間は増加しますが、最大時間ステップを減らすことにより改良されます。

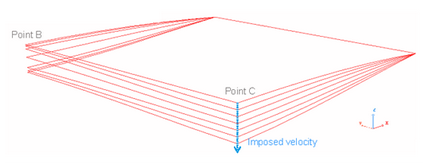
rad_ex_fig_2-10
図 5. スナップスルーの間の変形形状

陰解法と陽解法の比較結果

陰解法計算を通して得られた荷重変位曲線（時間ステップ限度を0 msに設定）と陽解法計算は非常に近くなっています。最大時間ステップ100 msでは荷重の非線形経路を正確に表現することはできません。しかし、最終静的荷重は正確です。

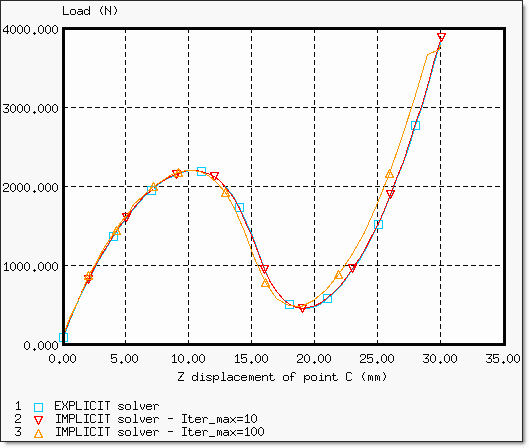
rad_ex_fig_2-11
図 6. 陰解法と陽解法で得られた荷重変位曲線
陽解法と陰解法（最大時間ステップを10 msに設定）アプローチの間の計算時間の比較を表 1に示します：
表 1. 計算時間
  陰解法ソルバー 陽解法ソルバー
正規化されたCPU 1 2.45
サイクル （正規化） 1 237

陰解法計算の比較で、最大時間ステップを10 msとした場合と、最大時間ステップを100 msに固定した場合で、節約されたCPU時間はおよそ4倍になっています。

参考文献

1 Finite Element Instability Analysis of Free Formed Shells.Report 77−2, 1977, Norwegian Institute Of Technology, Trondheim, HORRIGMOE G.