RD-E:1703 ゆがみ
スチール製のボックスビームが、一端を固定され、他端に無限の質量で衝撃を受けます。メッシュのゆがみによる結果の比較を行います。
スチール製のボックスビームが、一端を固定され、他端に無限の質量で衝撃を受けます。ボックスビームの寸法は203 mm x 50.8 mm x 38.1 mmであり、その板厚は0.914 mmです。対称性が考慮に入れられているため、構造の1/4のみがモデル化されます。4種類のメッシュと3種類の塑性定式化(グローバル塑性、 5積分点と反復塑性)が比較されます。
使用されるオプションとキーワード
- Q4シェル
- インターフェース(/INTER/TYPE7および/INTER/TYPE11)
構造の自己接触が構造全体でのTYPE7インターフェースを用いてモデル化されます。インターフェースのメインサーフェスはモデル全体を用いて定義されています。セカンダリ節点グループはメインサーフェスを用いて定義されます。
ビームの上部で、起こり得るエッジ-エッジ接触がTYPE11セルフインパクトインターフェースを用いて取り扱われます。そのエッジにはTYPE7インターフェースのメインサーフェスが入力のサーフェスとして用いられます。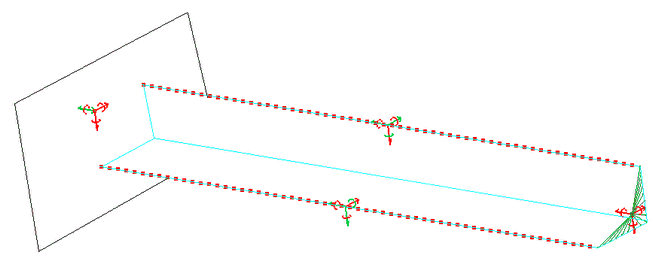
図 1. 境界条件 - グローバル塑性、反復塑性、可変板厚
- BT_TYPE1-3-4、QEPH、BATOZ、DKT18とC0定式化
- 境界条件(/BCS)
対称性を考慮して、Y-Z平面内の全ての節点はY方向並進とXとZ軸周りの回転が拘束されます。構造の1/4がモデル化されます。
- 剛壁(/RWALL)
インパクタはZ-方向の強制速度(13.3 m/s)を用いたスライド剛壁でモデル化され、他の並進と回転は固定されます。
- 強制速度(/IMPVEL)
- 剛体(/RBODY)
下(固定)端は、全ての下端の点(Z = 0.0)を結合する剛体を用いてモデル化されます。剛体は並進と回転が完全に拘束されます。
入力ファイル
必要なモデルファイルのダウンロードについては、モデルファイルへのアクセスを参照してください。
モデル概要
単位: mm、ms、g、N、 MPa
- 材料特性
- 初期密度
- 7.8 x 10-3
- ヤング率
- 210000
- ポアソン比
- 0.3
- 降伏応力
- 206
- 硬化パラメータ
- 450
- 硬化指数
- 0.5
- 最大応力
- 340
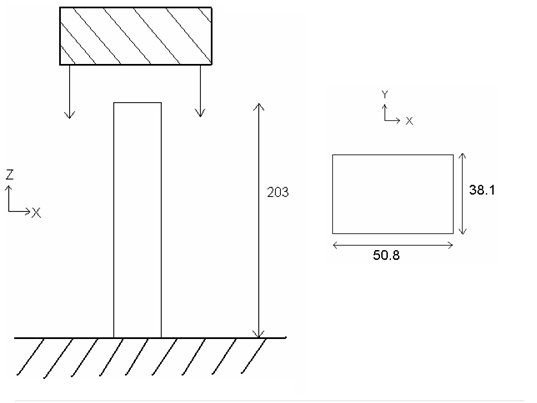
図 2. 検討された問題
モデリング手法
4つのビームが異なる周囲のメッシュでモデル化され、全て長さ方向に 56要素で高さ方向に8要素です。要素のレイアウトを図 3に示します。
- 要素定式化
- BT_TYPE1
- BT_TYPE3
- QEPH
- BATOZ
- C0
- DKT18
- 塑性:
- グローバル塑性
- 5積分点の漸進塑性
- 5積分点で反復塑性と可変板厚
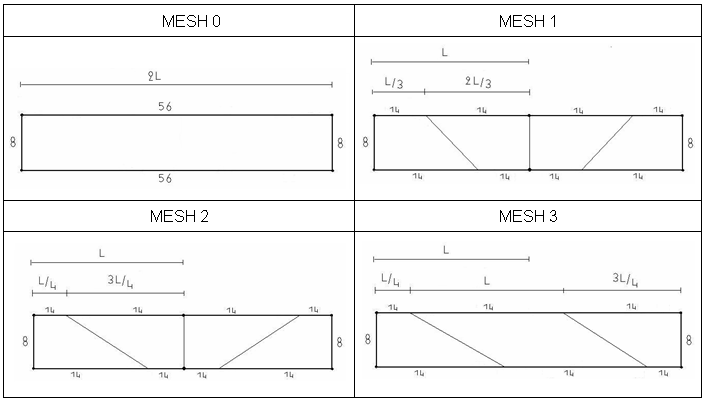
図 3. メッシュ
結果
- 与えられたタイプの要素定式化に対するメッシュの役割と影響。
- 与えられたメッシュに対するシェル要素定式化。
- 与えられたメッシュと要素定式化に対する塑性オプション。
- 圧壊力対変位
圧壊力はインパクタ(剛壁)のZ-方向の法線方向力に相当し、対称性から4倍されます。
比較では、剛壁のメイン節点のZ-方向移動が変位に相当します。
- アワグラスエネルギー
- 全エネルギー
全吸収エネルギーは内部エネルギーとアワグラスエネルギーの合計です。
グローバル塑性とBT_TYPE3定式化を用いて与えられたシェルのメッシュの影響
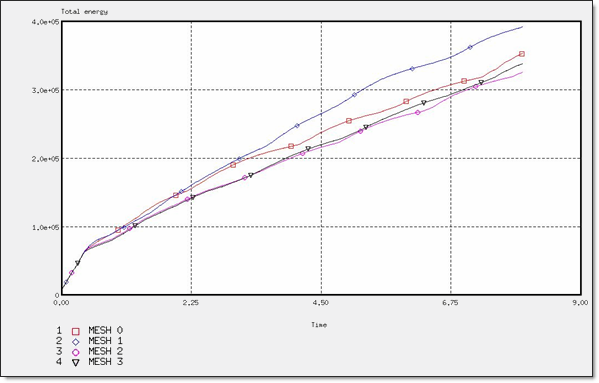
図 4. BT_TYPE3定式化での全エネルギー
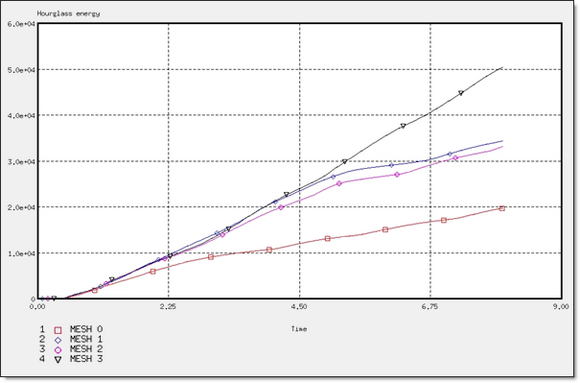
図 5. BT_TYPE3定式化でのアワグラスエネルギー
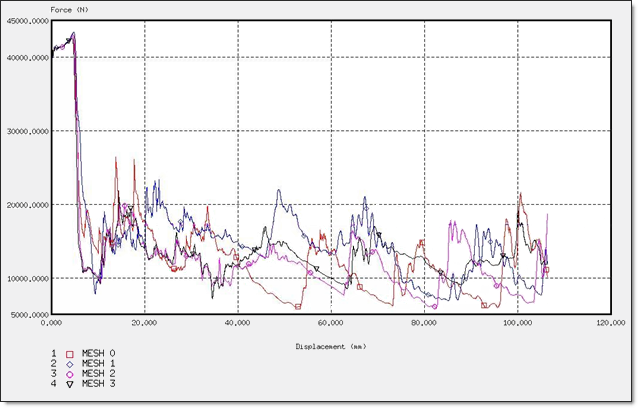
図 6. BT_TYPE3定式化での力
メッシュ1とグローバル塑性を用いた要素定式化の影響
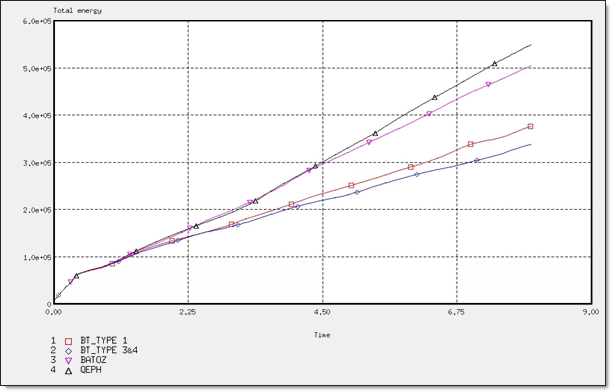
図 7. 異なる定式化での全エネルギー
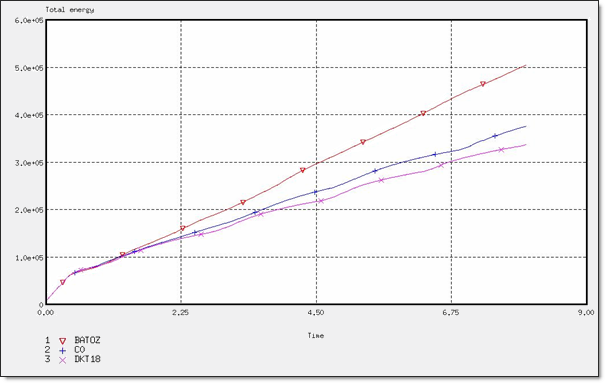
図 8. 異なる定式化での全エネルギー
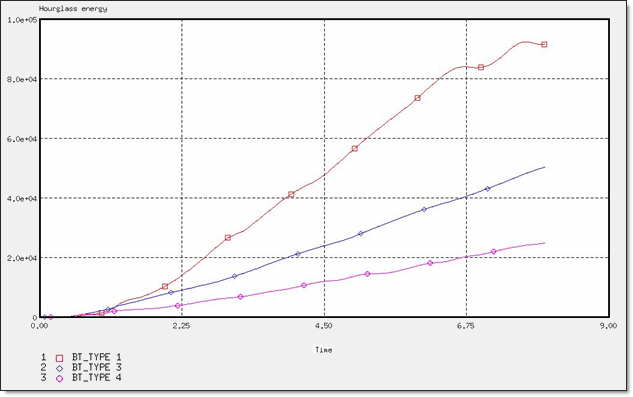
図 9. 異なるBT要素定式化でのアワグラスエネルギー
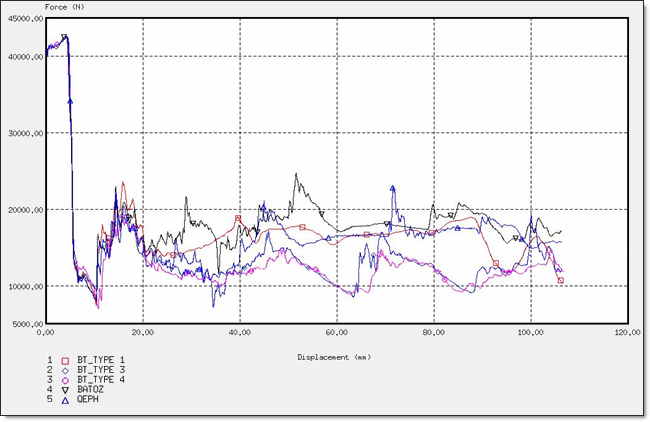
図 10. 異なる要素定式化での力
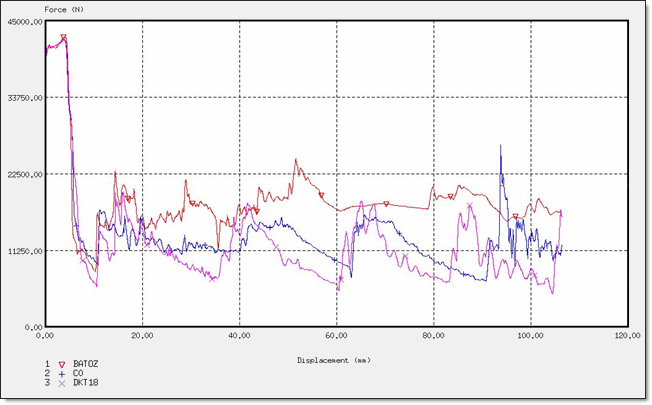
図 11. 異なる要素定式化での力
メッシュ0とBT_TYPE3定式化を用いた塑性オプションの影響
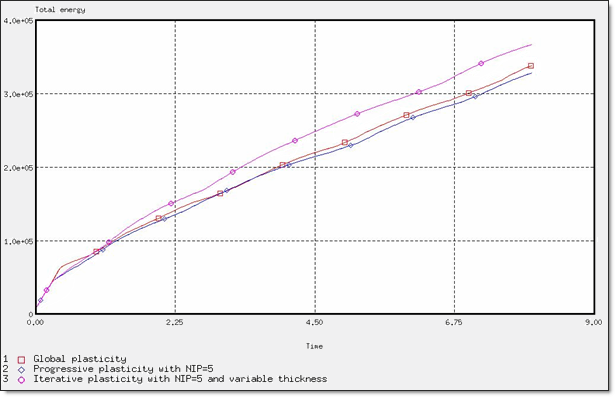
図 12. 全エネルギー
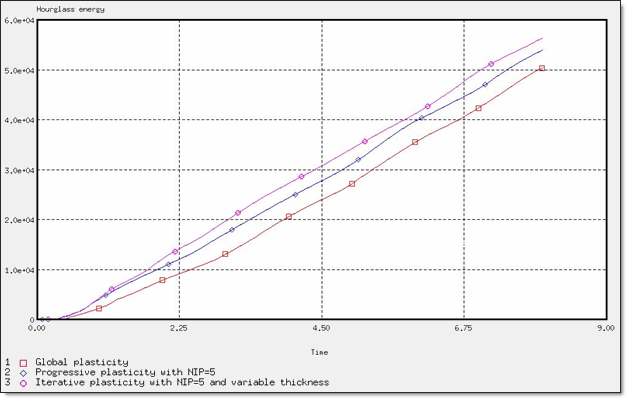
図 13. アワグラスエネルギー
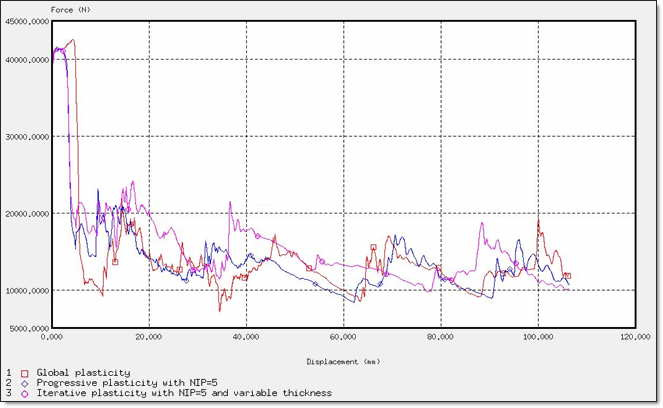
図 14. 圧壊力
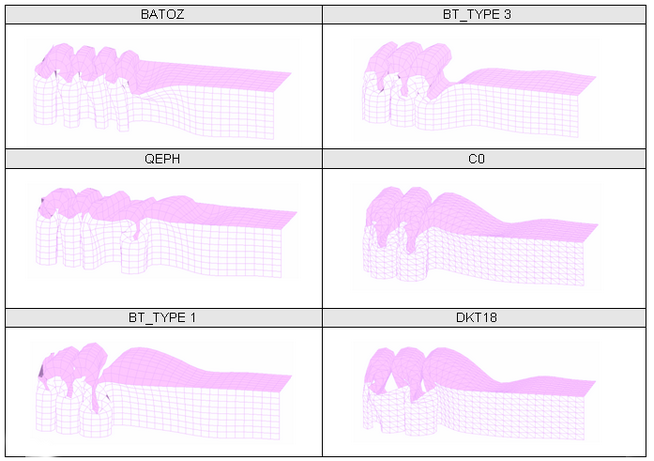
図 15. メッシュ 0
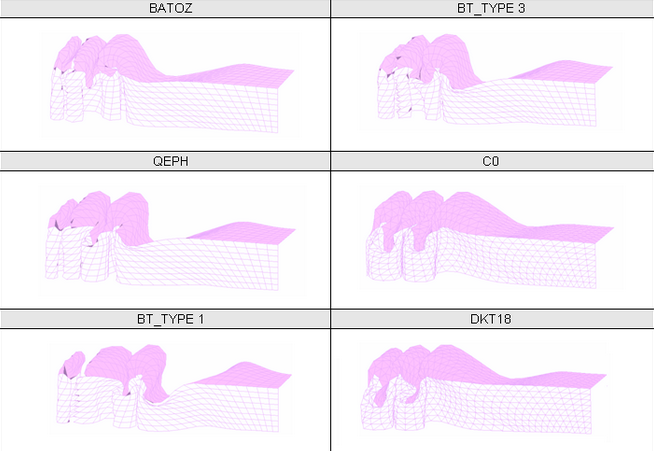
図 16. メッシュ 1
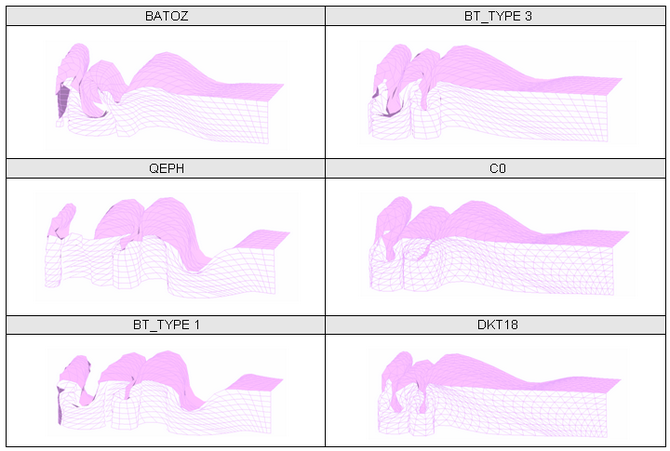
図 17. メッシュ 2
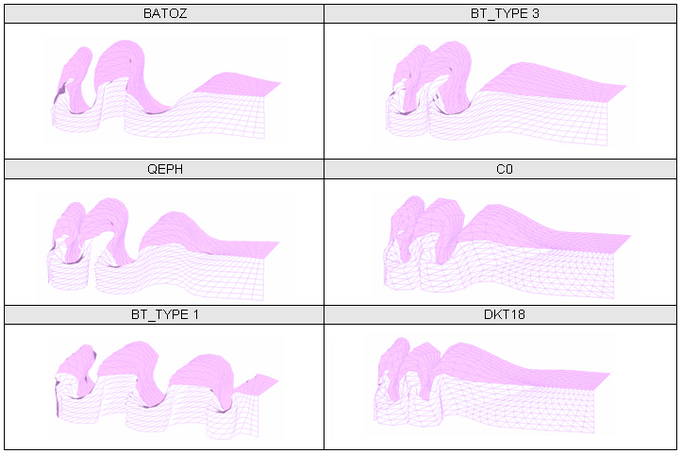
図 18. メッシュ 3
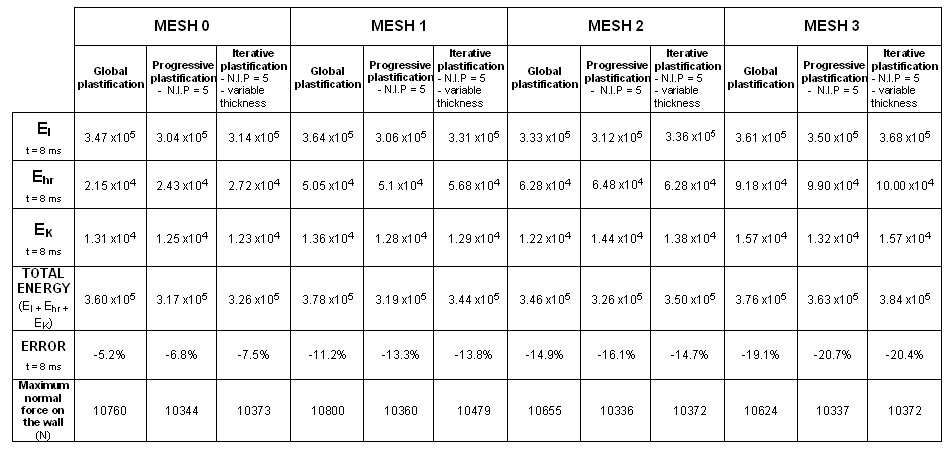
図 19. 定式化:BT_TYPE1
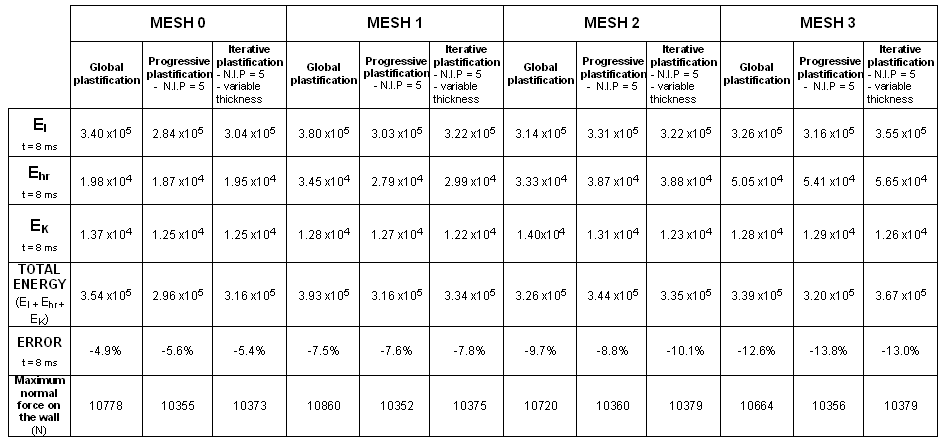
図 20. 定式化:BT_TYPE3
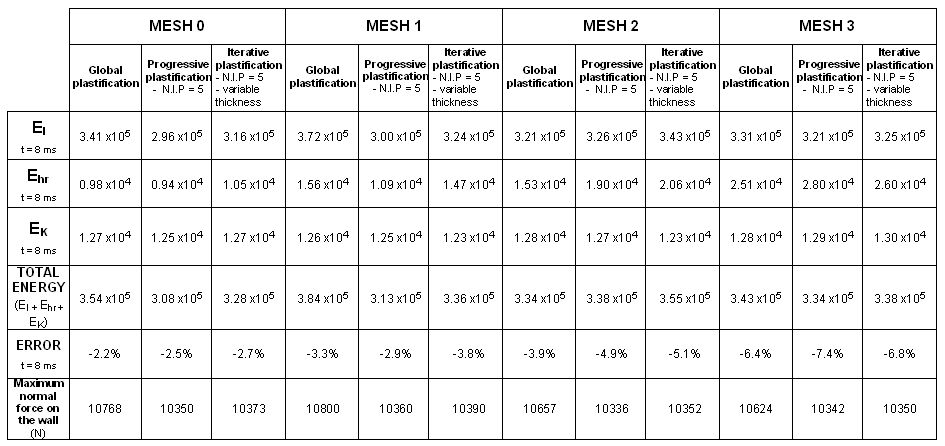
図 21. 定式化:BT_TYPE4
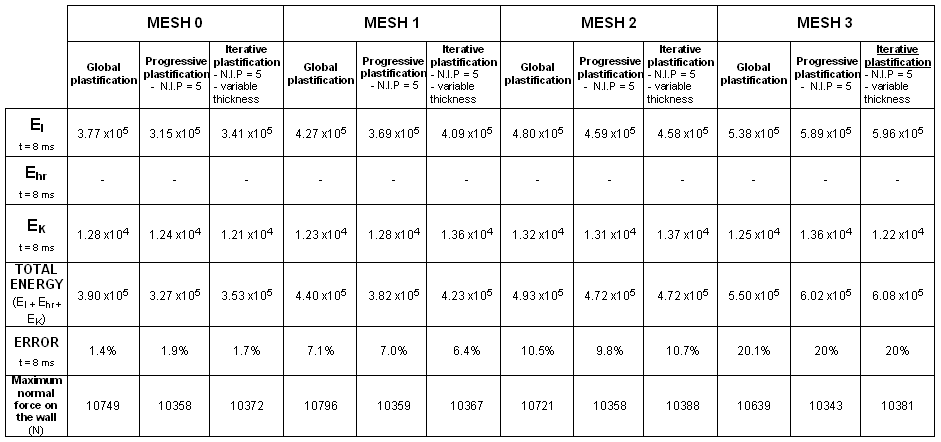
図 22. 定式化:QEPH
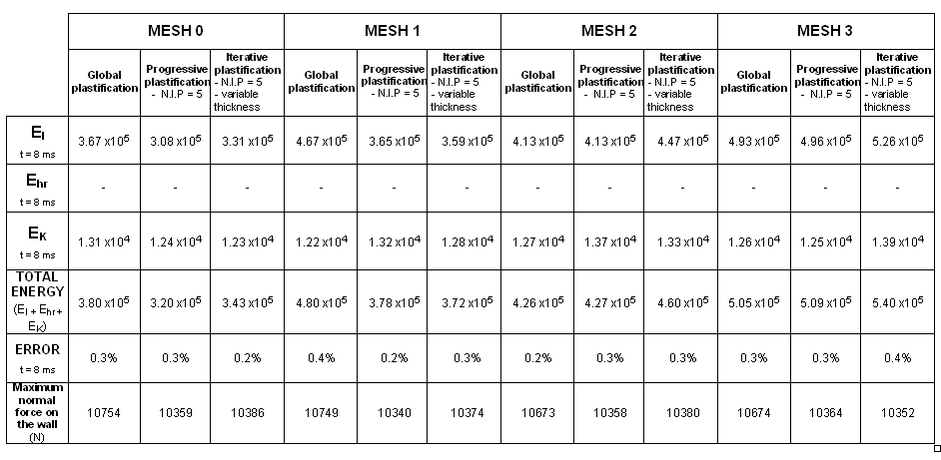
図 23. 定式化:BATOZ
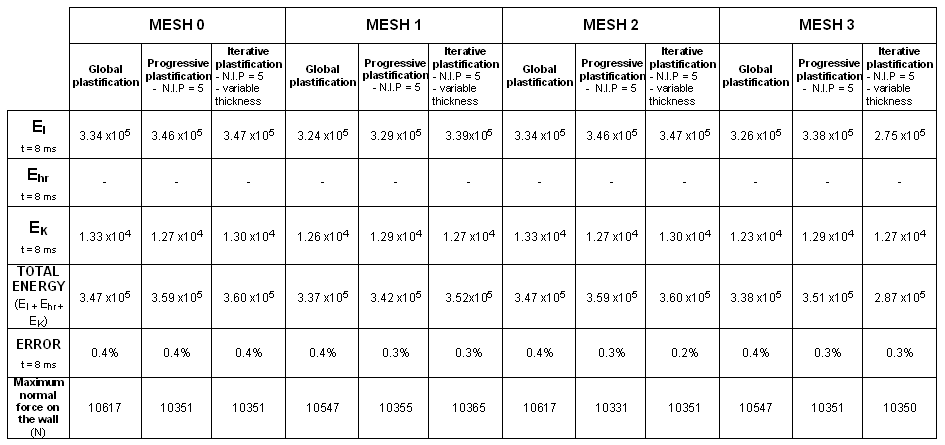
図 24. 定式化:DKT18
図 25. 定式化:C0
まとめ
ボックスビームの圧壊がいくつかのメッシュと要素定式化を用いて詳細に検討されました。一様、マッピングと遷移メッシュのシミュレーション結果が分類されそれぞれ異なる要素定式化に対して比較されています。得られた結果は、典型的な圧壊問題に対してのメッシュ品質に関するシェル要素の感度を示しています。