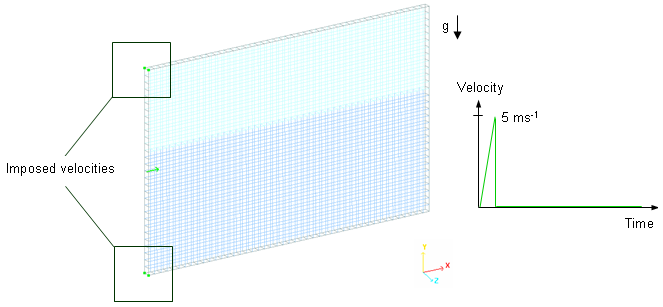
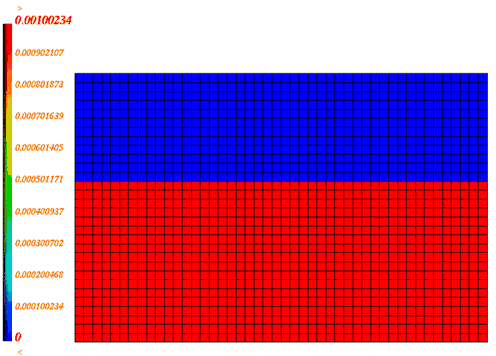
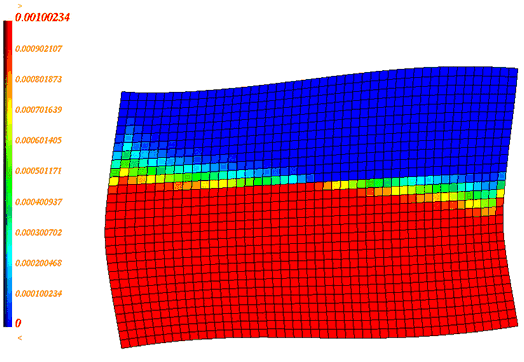
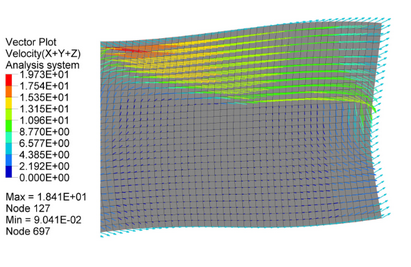
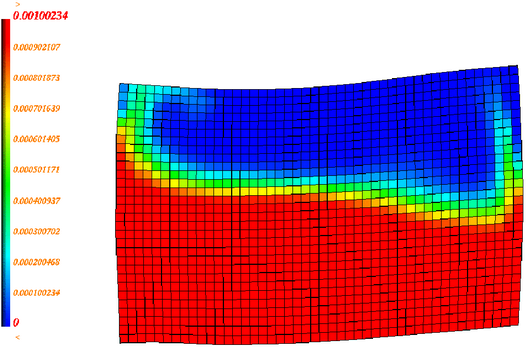
スチール製の矩形のタンクが部分的に水で満たされ、残りは空気で補充されています。初期の圧力分布は既知で一様であると仮定されます。タンクコンテナの寸法は460 mm x 300 mm x 10 mmで、板厚は2 mmです。
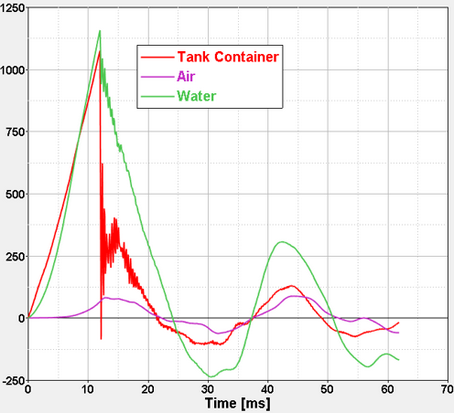
タンクコンテナの変形は、流体-構造連成を解析するためにタンクの左隅に与えられた衝撃により生じます。
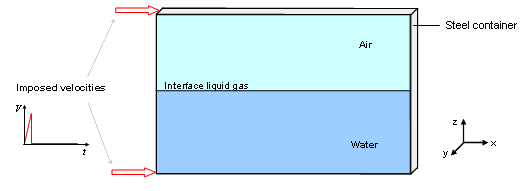
図 2. 問題の詳細
スチール製のコンテナはJohnson-Cook則の弾塑性モデル(
/MAT/LAW2)で以下のパラメーターを用いてモデル化されます:
- 材料特性
- 密度
- 0.0078
- ヤング率
- 210000
- ポアソン比
- 0.29
- 降伏応力
- 180
- 硬化パラメータ
- 450
- 硬化指数
- 0.5
気体-液体の2相の材料はALE RADIOSSドキュメントで利用可能な流体2相流体-気体則(/MAT/LAW37)で記述されます。材料則LAW37は流体-気体2相のモデル化に特化して設計されています。
粘性と圧力の状態を記述するために用いられる式は:
- 粘性
- 流体の状態方程式
- ここで、かつ
- 気体の状態方程式
- ここで、特定の体積として
つり合いは以下のように定義されます:
ここで、
- 偏差応力テンソル
- 偏差ひずみテンソル
- 材料パラメータ - 流体に対して
- 液体の基準密度
- 0.001
- 液体の弾性率
- 2089 N/mm2
- 初期液体質量比率
- 100%
- せん断動粘性、、
- 0.001 mm2/ms
- 材料パラメータ - 気体に対して
- 液体の基準密度
- 1.22x10-6
- せん断動粘性、、
- 0.00143 mm2/ms
- 完全気体定数
- 1.4
- 初期圧力参照気体、
- 0.1 N/mm2
空気 / 水パートの主なソリッドTYPE14プロパティは:
- プロパティ
- 2次体積粘性 / 線形体積粘性
- 10-20
- アワグラス体積係数
- 10-5
モデリング手法
空気と水はALE定式化と2相材料則(
/MAT/LAW37)を用いてモデル化されます。タンクコンテナはLagrange定式化を用い、弾塑性材料則(
/MAT/LAW2)が用いられます。
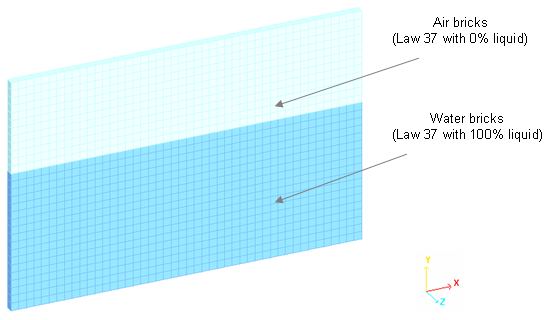
図 3. 空気と水のメッシュ(ALEソリッド要素)
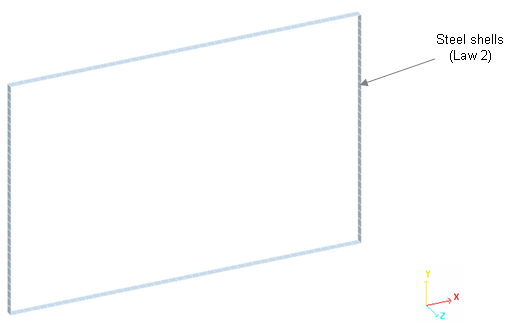
図 4. タンクコンテナのメッシュ(シェル要素)
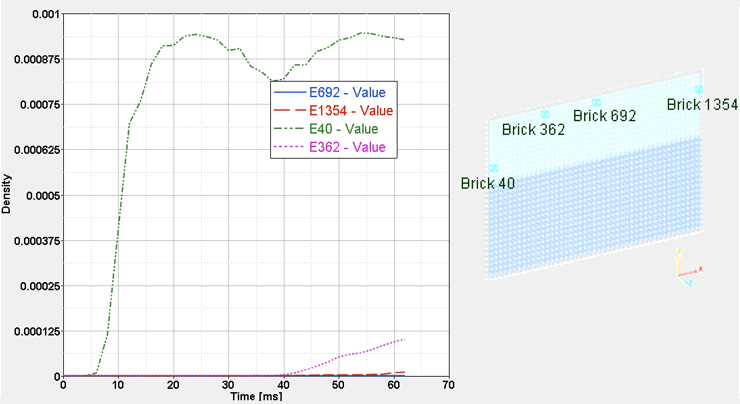
ALE定式化を用い、ソリッドメッシュはタンクの変形によってのみ変形し、水がメッシュ内を流れます。Lagrangeシェル節点は材料のポイントに一致し、要素は材料と共に変形します。これはLagrangianメッシュと呼ばれます。ALEメッシュでは、境界上の節点は境界に留まるために固定され、内部節点が移動します。