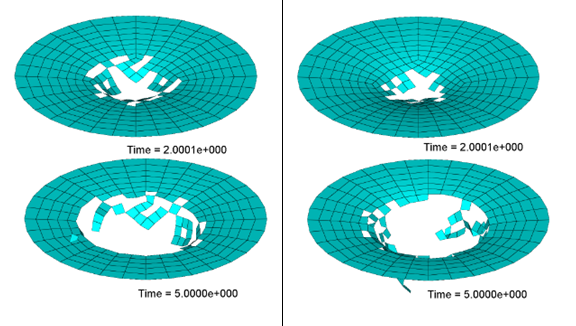
1つのシェル要素を使用して、この破断モデルを表現します。
このモデルの材料は、Johnson-Cookモデルで再現できる等方性弾塑性挙動を示します。
材料特性は:
- ヤング率
- 71000
- ポアソン比
- 0.3
- 密度
- 2.8 x 10-3 g/mm3
- 降伏応力
- 290
- 硬化パラメータ
- 562.3
- 硬化指数
- 0.63
- 最大応力
- 425
最大応力と破壊ひずみは破壊モデリングのセクションで考慮されます。この例題ではひずみ速度効果は考慮されません。LAW2とLAW27のいずれでも、弾塑性の挙動にJohnson-Cook材料モデルを使用していますが、材料で使用している破断定義はそれぞれ異なっています。
LAW2: 破断に塑性ひずみを使用
LAW2では、要素の破断に最大塑性ひずみ
を使用しています。したがって、材料のひずみが、モデルに定義された最大塑性ひずみに達すると、シェル要素が削除されます。LAW27と異なり、破断の前にダメージが始まることはなく、引張と圧縮の両方で破断が発生します。
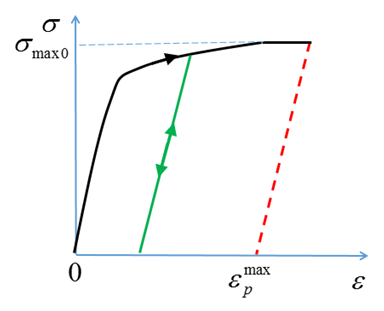
図 1. 最大塑性ひずみに達するLAW2の応力 / ひずみ曲線
LAW27: ダメージモデルを使用
LAW27は、Johnson-Cook則を使用した材料ダメージのシミュレートに使用します。ダメージモデルが材料則に導入され、要素の破断で応力が減少する時点までダメージの進行が考慮されます。LAW27に記述された材料破断を使用すると、破断とダメージは引張でのみ発生し、圧縮では発生しません。
主方向のダメージパラメータはで、値は次のようになります。
; ;
主ひずみが
に達すると、ダメージ面の
と
に基づいて材料のダメージが始まります。この2つの値は次の式で与えられます。
(1)
は方向を指定します。
つづいて、ダメージパラメータ.を使用することで応力が減少します。
第1の主方向のダメージ係数は、次のように主ひずみの関数になります。
(2)
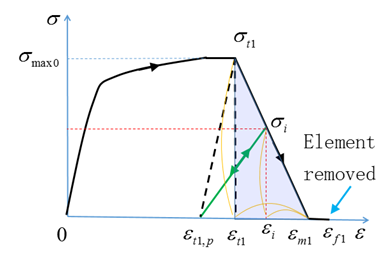
図 2. ダメージが材料に与えられた時の応力 / ひずみ曲線



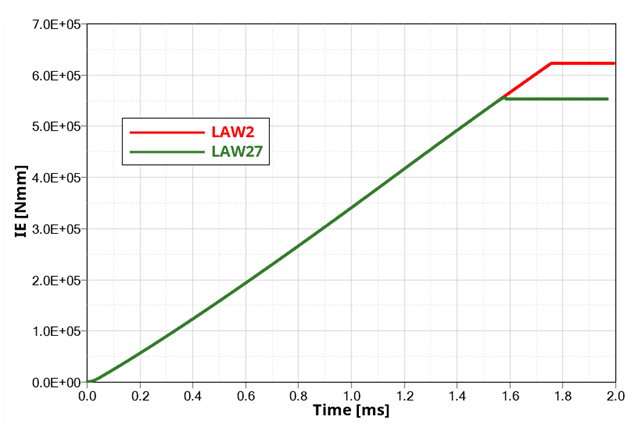
 等二軸負荷では、LAW2とLAW27で破断の処理が異なることから、それぞれで要素の削除時点が異なります。LAW2では、要素のひずみがに達すると要素が削除されます。塑性ひずみの変化は次のようになります。
等二軸負荷では、LAW2とLAW27で破断の処理が異なることから、それぞれで要素の削除時点が異なります。LAW2では、要素のひずみがに達すると要素が削除されます。塑性ひずみの変化は次のようになります。