Reference: Solver Variable
Model ElementReference_Variableは、MotionSolveで代数状態を定義します。
説明
- 直接システム状態と時間の明示的な関数として。
- 直接システム状態と時間の暗黙的な関数として。
- 拘束またはペナルティとして適用される代数方程式を介して間接的に。
- 式の積分として。
Reference_Variablesは非常に用途が広いため、マルチボディシステムのモデル化において、さまざまな用途に適用できます。これらは、シミュレーションで注目する信号の作成に使用されます。その後信号は、力の定義、テストデータへの補間のための独立変数の作成、一般的な制御要素への入力の定義、および複雑な出力信号の作成に使用されます。
フォーマット
<Reference_Variable
id = "integer"
[label = "string"]
{
type = "EXPRESSION"
expr = "motionsolve_expression"
type = "USERSUB"
usrsub_dll_name = "valid_path_name"
usrsub_fnc_name = "custom_fnc_name"
usrsub_param_string = "USER(par_1, ..., par_n)"
type = "USERSUB"
script_name = "valid_path_name"
interpreter = "PYTHON" | "MATLAB"
usrsub_fnc_name = "custome_fnc_name"
usrsub_param_string = "USER(par_1, ..., par_n)"
}
[[
is_implicit = "true" | "false"
autobalance = "default" | "conditional" | "disabled" | "penalty"
penalty = "double"
penalty1 = "double"
dot_form = "true" | "false"
[[ic = "real" ]]
[[static_hold = "true" | "false"]]
]]
/>属性
- id
- 要素識別番号（整数 > 0）を指定します。この番号は、すべてのReference_Variable要素の中で一意です。
- label
- この属性は、Reference_Variable要素の名前を説明します。この説明は、主に、入力を読みやすくするために使用します。
- type
-
EXPRESSIONまたはUSERSUBを選択します。変数式の定義方法を指定します。
- EXPRESSIONオプションは、Reference_Variableの値が実行時に評価できるMotionSolveの式であることを指定します。
- USERSUBオプションは、イベントの値がユーザー定義のサブルーチンで指定されることを示します。パラメータ“usrsub_param_string”および“usrsub_dll_name”は、このユーザー定義サブルーチンに関する詳細情報を提供するために使用されます。
- expr
- Reference_Variableを定義するMotionSolve式を指定します。このパラメータは、type = EXPRESSIONである場合にのみ使用します。任意の有効な実行時MotionSolve式を入力として指定できます。
- usrsub_dll_name
- ユーザーサブルーチンを含むDLLまたは共有ライブラリのパスと名前を指定します。MotionSolveはこの情報を使用して、実行時にDLL内のユーザーサブルーチンを読み込みます。このキーワードは、type = USERSUBの場合にのみ使用します。
- usrsub_fnc_name
- このパラメータにより、ユーザーサブルーチンの名前を指定できます。この属性が指定されない場合は、デフォルト名VARSUBが使用されます。このキーワードは、type = USERSUBの場合にのみ使用します。
- usrsub_param_string
- データファイルからユーザー定義のVARSUBに渡されるパラメータのリスト。このキーワードは、type = USERSUBの場合にのみ使用します。
- script_name
- usrsub_fnc_nameで指定された関数を含むユーザー作成スクリプトのパスと名前を指定します。このキーワードは、type = USERSUBの場合にのみ使用します。
- interpreter
- ユーザースクリプトが記述されたインタープリタ型言語を指定します。有効な選択肢は、MATLABまたはPYTHONです。
- is_implicit
- デフォルトで、すべてのReference_Variablesは明示的に指定されます。このキーワードは、変数が暗黙的に定義されることを示すために使用されます。この詳細については、コメント2および3をご参照ください。
- auto_balance
-
この属性は、変数が代数的な関係を定義する場合に、MotionSolveにLagrange乗数の処理方法を指示します。
- “Conditional”は、MotionSolveがハードな拘束を実装し、Lagrange乗数が解析プロセスの一部として計算されることを意味します。有限差分がGTCMAT内で実行される場合を除き、Lagrange乗数によって計算された拘束の反力および反トルクは自動的に適用されます。
- “Unconditional”は、MotionSolveがハードな拘束を実装し、Lagrange乗数が解析プロセスの一部として計算されることを意味します。Lagrange乗数によって計算された拘束の反力および反トルクは、自動的に例外なく無条件に適用されます。
- “Disabled”は、MotionSolveが拘束方程式を実装するのみであることを意味します。Lagrange乗数による一般化反力は運動方程式に適用されません。等価な力を適用してこれを行う必要があります。
- “Penalty”は、MotionSolveがペナルティ定式化を使用して拘束を実装することを意味します。詳細については、コメント3をご参照ください。
MotionSolveのデフォルトの挙動は、“conditional”です。
- penalty
- auto_balance=penaltyの場合にのみ使用されます。拘束の適用に使用される復元力の計算に使用するペナルティ係数を指定します。詳細については、コメント3をご参照ください。
- penalty1
- auto_balance=penaltyの場合にのみ使用されます。拘束の適用に使用される復元力の計算に使用する2番目のペナルティ係数を指定します。詳細については、コメント3をご参照ください。
- dot_form
- exprで定義された値の積分を、Reference_Variableの値として使用するように指定します。
- ic
- dot_form = “True”の場合のみ使用する必要があります。Reference_Variableが積分形式で定義されている場合は、初期値が必要です。IC属性を使用して、Reference_Variableの初期値を指定します。ICが指定されていない場合、デフォルトで0になります。
- static_hold
- dot_form = “True”の場合のみ使用する必要があります。Static_Holdは、静的平衡反復計算時に、Reference_Variableの値をICの値に固定するように指定します。指定されない場合、MotionSolveは必要に応じて変数の初期値を変更します。
例1
この例では、EXPRESSIONベースのReference_Variableを使用して、剛体の運動エネルギーを計算する方法を示します。下の例で、Reference_VariableのIDは3070です。1011は、質量4kg、主慣性モーメントIxx=0.006Kgm2、Iyy=0.005Kgm2、およびIzz=0.004Kgm2の剛体の質量中心を定義するMARKERです。Reference_Variable 3070は、剛体の総運動エネルギーです。
<Reference_Variable
id = "3070"
type = "EXPRESSION"
expr = "0.5*(4*VM(1011)**2 + 0.006*WX(1011)**2 + 0.005*WY(1011)**2 + 0.004*WZ(1011)**2)"
/>例2
2番目の例は、最初の例と同じことをしていますが、ユーザーサブルーチン内に実装されています。任意の剛体の運動エネルギーを計算できるユーザー定義サブルーチンVARSUBが最初に記述されています。VARSUBへの入力パラメータは、剛体の質量と慣性のプロパティ、および質量中心マーカーのIDです。VARSUBは、剛体の運動エネルギーを返します。これは、任意の剛体の運動エネルギーを計算できるジェネリック関数です。
<Reference_Variable
id = "3070"
type = "USERSUB"
usrsub_param_string = "USER (1011, 4, 0.006, 0.005, 0.004)"
usrsub_dll_name = "/Users/ms_test/ke.dll"
usrsub_fnc_name = "Kinetic_Energy"
/>Pythonで記述されたVARSUBを以下に示します。
from math import *
def VARSUB(id, time, par, npar, dflag, iflag):
# Get information from the par array
icm = 1*[0]
icm[0] = par[0]
mass = par[1]
ixx = par[2]
iyy = par[3]
izz = par[4]
# get the translational and rotational velocity states
[vm,errflg] = py_sysfnc ("VM", icm)
[w, errflg] = py_sysary ("RVEL", icm)
# Calculate the kinetic energy
if iflag:
KE = 0.0
else:
KE = 0.5 * (mass*vm**2 + ixx*w[0]**2 + iyy*w[1]**2 + izz*w[2]**2)
return KE例3
3番目の例は、システム内の1点に拘束が適用されているが、反力が別のポイントで要求される、単純な2Dの例を示しています。 図 1 は、地面に固定された2Dロボットを表しています。ロボットのエンドエフェクターTは、図のように2D空間内のパスをトレースする必要があります。Spline/1とSpline/2で、それぞれF(t)とg(t)が指定されます。パラメータtは、システムシミュレーション時間を表します。モデル内で、Reference_Marker 11は、エンドエフェクターの先端を表します。
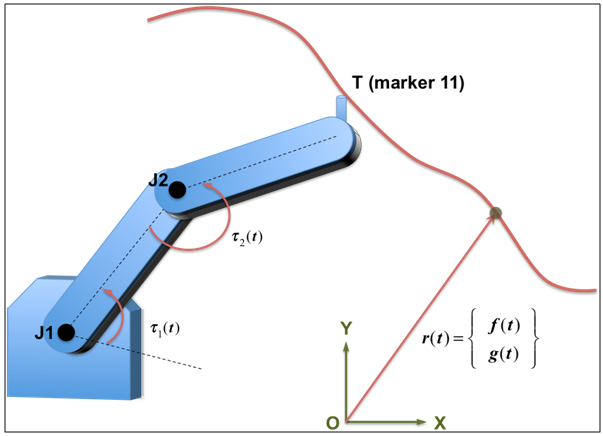
図 1. 空間内の複雑な2Dパスを辿る必要のある2Dロボット
さまざまなボディに質量と慣性のプロパティがあり、これらによって適切に形状が定義されています。この例では、これらに関係性はありません。ただし、これらはモデル内の別の場所で定義される必要があることに注意することが重要です。
ロボットの設計者は、システム内の回転ジョイントJ1およびJ2で作用するモーターのサイズを指定する必要があります。モーターのサイズを指定するには、これらのジョイントに適用されるトルクを把握する必要があります。拘束を定義するため、3つのMotion_Markersを作成する場合、MotionSolveは、J1およびJ2に適用されるトルクではなく、エンドエフェクターの先端での力を計算します。
- マーカー11のモーションを定義する2つの代数拘束を定義します。
<Reference_Variable |<Reference_Variable id = "1" | id = "2" type = "EXPRESSION" | type = "EXPRESSION" expr = "DX(2011) - cubspl(time, 0, 1)" | expr = "DY(2011) - cubspl(time, 0, 2)" is_implicit = "True" | is_implicit = "True" autobalance = "Disabled" | autobalance = "Disabled" /> |/> - ジョイントJ1とJ2にトルクとして内力を適用します。
J1はIマーカー=33、Jマーカー=44、J2はIマーカー=55、Jマーカー=66で定義されるとします。また、地面座標系はマーカーID=77で表されるとします。
<Force_Vector_TwoBody | <Force_Vector_TwoBody id = "1" | id = "2" type = "TorqueOnly" | type = "TorqueOnly" i_marker_id = "33" | i_marker_id = "55" j_floating_marker_id = "44" | j_floating_marker_id = "66" ref_marker_id = "77" | ref_marker_id = "77" tx_expression = "0" | tx_expression = "0" ty_expression = "0" | ty_expression = "0" tz_expression = "VARVAL(1)" | tz_expression = "VARVAL(2)" /> | /> - モーターのサイズを指定するジョイントに適用されるトルクを確認します。
Varval(1)およびVarval(2)が、それぞれジョイントJ1およびJ2に適用されるトルクです。
例4
この例は、Reference_Variablesを使用して、MATLABで定義した制御システムのPlant_Inputsを定義します。スライダーに取り付けられた倒立振り子を安定化するという制御問題について考えてみましょう。次の図は、その構成の一例を示しています。スライダー（緑のブロック）は、グラウンド（赤い細片）に対する並進ジョイントによって全体座標系のx軸に沿って動くように拘束されています。
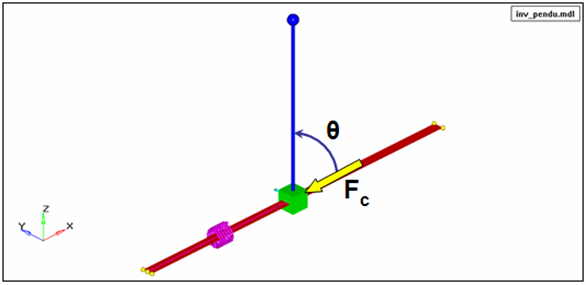
図 2. 倒立振り子モデル
- プラント入力：スライダーに作用する制御力Fc。これはMATLABにより計算され、MotionSolveに送信されます。
- プラント出力：振り子角度θおよび角速度ω。これらの信号はMATLABに送信されます。
プラント出力は次のように定義できます：
<Control_PlantOutput
id = "303001"
num_element = "2"
variable_id_list = "12", "13"
hold_order = "1"
/>Reference_Variable 12は振り子角度θを定義し、Reference_Variable 13は振り子の角速度ωを定義します。Reference_Variablesは、次のように定義されます。
<Reference_Variable |<Reference_Variable
id = "12" | id = "13"
type = "EXPRESSION" | type = "EXPRESSION"
expr = "-AY(1011,2011)" | expr = "-WY(1011,2011)"
/> |/>例5
この例は、自動車モデルでステアリングギア比を定義するために使用する変数を示しています。ステアリング比とは、ステアリングホイールの回転数とホイールの回転数の比率です。ステアリング比が高いと、特定のホイールの回転を得るためにステアリングホイールをより多く回転させる必要がありますが、ステアリングホイールを回転させることは容易になります。ステアリング比が低ければ、この逆になります。
この演習の目的は、ステアリングホイール角が指定されている場合に、Reference_Variableを使用してステアリング比を定義することです。この比率が定義されると、下流でこれを使用してホイールに適切なトルクを適用することができます。
ステアリングホイール上の回転ジョイントが、Iマーカー=6565、Jマーカー=7676で定義されるとします。ステアリング角とステアリングギア比を定義する変数を以下に示します。
<Reference_Variable | Reference_Variable
id = "1" | id = "2"
label = "Steering angle in degrees" | label = "Steering gear ratio"
type = "EXPRESSION" | type = "EXPRESSION"
expr = "RTOD * ABS(AZ(6565,7676))" | expr = "step(varval(1), 100, 1000, 150, 1500)"
/> | />
図 3. ステアリングギア比対ステアリング角
例6
Reference_Variableにより、ペナルティオプションを使用して“ソフト拘束”を定義します。これを説明するため、簡単な例をここに示します。
下の図 4に示すように、マーカー11のz軸とマーカー21のz軸の間の角度を60度に維持する状況について考えます。
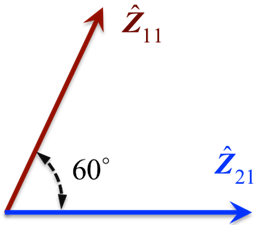
図 4. 2つのマーカーのz軸間の角度
General_Constraintを使用して、この拘束を定義できます。ただし、モデル内にシステムの弾性を組み込みたい場合は、一部の違反が許容されるように“ソフト拘束”として運動条件をモデル化します。
<Reference_Variable | The torque that is implemented
id = "1" |
label = "A soft constraint" |
type = "EXPRESSION" |
expr = "theta(21,11) - 60D |
is_implicit = "TRUE" |
autobalance = "PENALTY" |
penalty = "1000.0" |
penalty1 = "10.0" |
/> <Force_Penalty | The torque that is implemented
id = "1" |
label = "A soft constraint" |
type = "EXPRESSION" |
expr = "theta(21,11) - 60D" |
penalty = "1000.0" |
penalty1 = "10.0" |
/>コメント
- 直接的で明示的な変数は、varval = g(y,t)として定義されます。varvalは変数の値、yはシステム状態に依存する値の任意のセットです。式またはユーザーサブルーチンで、関数g(y,t)を定義します。
- 直接的で暗黙的な変数は、g(varval,y,t)=0として定義されます。繰り返しになりますが、varvalは変数の値、yはシステム状態に依存する値の任意のセットです。式またはユーザーサブルーチンで、関数g(varval, y,t)を定義します。このタイプの変数の場合、varvalは、関数g(...)で明示的に参照される必要があります。
- 代数拘束は、g(y,t)=0のように定義されます。yは、システム状態依存の変位値の任意のセットです。式またはユーザーサブルーチンで、関数g(y,t)を定義します。このタイプの変数の場合、varvalは、関数g(...)で明示的に参照されることはありません。varvalは、Lagrange乗数です。これは、拘束g(y,t)=0を維持するために必要な内力を表します。g(y,t)=0は、ハード拘束として適用できます。この場合、varvalはシステム未知数で、MotionSolveによって決定されます。代わりに、ペナルティ関数を介して、g(y,t)=0を“ソフト”拘束として適用することもできます。この場合、varvalは拘束値g(y,t)を返し、この拘束違反がMotionSolveによって強制されたり監視されたりすることはありません。人工的なLagrange乗数は、-penalty*g(y,t)-penalty1*ġ(ẏ,y,t)として計算されます。ここで、ġ(...)=
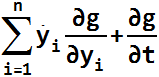です。また、このLagrange乗数によって計算された拘束の反力および反トルクは、自動的にマルチボディシステムに適用されます。auto_balance=penaltyの詳細については、Force_Penaltyをご参照ください。 - 変数は、積分形式で次のように定義できます：
ż = g(y,t); varval = zvarvalは変数の値（g(y,t))の積分）、yはシステム状態に依存する値の任意のセットです。式またはユーザーサブルーチンで、関数g(y,t)を定義します。
- 関数g(y,t)を定義するには、次の3つの手法を使用できます。
- XMLファイル内の関数式として：これは最も簡単な方法であり、関数式言語に組み込まれた関数と演算子で構成された式としてg(y,t)が定義されます。
- DLLで指定されるユーザー作成のコンパイルされたサブルーチンとして：任意の言語を使用できます。MotionSolveでは、Fortran、C、およびC++のインターフェースを用意しています。ユーザー作成のサブルーチンのデフォルト名はVARSUBです。ただし、この関数に任意の名前を付け、MotionSolveにその名前を伝えることができます。
- PythonまたはMATLABで記述されたスクリプトとして：この手法は、コンパイルされた言語でユーザー作成のサブルーチンを記述するより効率は下がりますが、次の2つの大きな利点があります：（A）関数g(y,t)を構成するために、関数式に比べてはるかに柔軟で強力な環境を提供します。（B）Fortran、C、またはC++を使用する場合に、コンパイラやリンカーが必要ありません。
- 積分器がABAM、VSTIFF、またはMSTIFFの場合、変数の再帰的な定義はできません。
- MotionSolveの入力言語では、Reference_Variablesを使用して次の要素を定義します：Control_PlantInput、Control_PlantOutput、Reference_Array。
- 一般に、関数式でReference_Variableを使用して、MOTIONモデリング要素を定義することはお勧めしません。
- ユーザーサブルーチンVARSUBを使用して、離散的な代数状態（言い換えると、特定のサンプル時間にのみ変化する状態）を定義できます。ただし、ユーザー定義サブルーチン内で、サンプリングおよび更新アクションを管理するためのロジックを実装する必要があります。