Control: State Equation
Model ElementControl_StateEqnは、一般的な動的システムを定義する抽象モデリング要素です。動的システムは、入力のベクトルu、動的状態のベクトルx、および出力のベクトルyによって表現されます。状態ベクトルxは、微分方程式のセットを通じて定義されます。
説明

図 1. 動的システムの入力、出力および状態
MotionSolveでは、2つのタイプのControl_StateEqn要素を使用できます。
- 線形動的システム:これらは4つのマトリクスA、B、C、Dで表現されます。これらは、次のように動的システムに関連付けられます:
(1) 4つのマトリックスA、B、C、Dはすべて定数値です。最初の式は状態を定義し、2番目の式は出力を定義します。
Aマトリクスは状態マトリクスと呼ばれ、システムの特性を定義します。“n”個の状態がある場合、Aマトリクスの次元はn x nとなります。AまたはBまたはA+Bのいずれかが正則である必要があります。
Bマトリクスは入力マトリクスと呼ばれ、入力が状態に与える影響を定義します。“m”個の入力がある場合、Bマトリクスのサイズはn x mとなります。
Cマトリクスは出力マトリクスと呼ばれ、状態が出力に与える影響を定義します。“p”個の出力がある場合、Cマトリクスのサイズはp x nとなります。
Dマトリクスは直接フィードスルーマトリクスと呼ばれ、入力が直接出力に与える影響を定義します。Dマトリクスのサイズはp x mとなります。
- 非線形動的システム:これらは、F()とG()の2つのベクトル関数で表現されます。これらは、次のように動的システムに関連付けられます:
(2) 関数F()は、x(t)とu(t)が与えられると、xの時間導関数を返します。関数G()は、x(t)とu(t)が与えられると、出力yを返します。F()とG()はどちらも、ユーザー定義のサブルーチンで定義する必要があります。
フォーマット
<Control_StateEqn
id = "integer"
[ label = "string" ]
x_array_id = "integer"
ic_array_id = { "integer" | "0" }
[ is_static_hold = { "TRUE" | "FALSE" } ]
[ y_array_id = "integer" ]
[ u_array_id = "integer" ]
{
type = "LINEAR"
a_matrix_id = "integer"
[ b_matrix_id = "integer" ]
[ c_matrix_id = "integer" ]
[ d_matrix_id = "integer" ]
| type = "USERSUB"
num_state = "integer"
num_output = "integer"
usrsub_param_string = "USER([[par_1[,...][,par_n]])"
usrsub_dll_name = "valid_path_name"
[ usrsub_fnc_name = "custom_fnc_name" ]
[ usrsub_der1_name = "custom_fnc_name" ]
[ usrsub_der2_name = "custom_fnc_name" ]
[ usrsub_der3_name = "custom_fnc_name" ]
[ usrsub_der4_name = "custom_fnc_name" ]
| type = "USERSUB"
num_state = "integer"
num_output = "integer"
script_name = valid_path_name
interpreter = "PYTHON" | "MATLAB"
usrsub_param_string = "USER([[par_1[,...][,par_n]])"
[ usrsub_fnc_name = "custom_fnc_name" ]
[ usrsub_der1_name = "custom_fnc_name" ]
[ usrsub_der2_name = "custom_fnc_name" ]
[ usrsub_der3_name = "custom_fnc_name" ]
[ usrsub_der4_name = "custom_fnc_name" ]
>
}
</Control_StateEqn>属性
- id
- 要素識別番号(整数 > 0)。これは、すべてのControl_StateEqn要素の中で一意の番号です。
- label
- Control_StateEqn要素の名前。
- is_static_hold
- 静的平衡解析および擬似静解析の間、動的状態の値xを固定するかどうかを指定するブール値。
"TRUE"は、静解析および擬似静解析の間、動的状態が一定に保たれることを意味します。
"FALSE"は、静的平衡解析または擬似静解析の間、動的状態が変化可能であることを意味します。 5
- x_array_id
- このControl_StateEqnの状態“x”を格納するために使用するREFERENCE_ARRAYのIDを指定します。このIDを持つARRAY()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの状態値にアクセスすることもできます。
- y_array_id
- このControl_StateEqnの出力“y”を格納するために使用するREFERENCE_ARRAYのIDを指定します。このIDを持つARRAY()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの出力値にアクセスすることもできます。
- u_array_id
- このControl_StateEqnの入力u を格納するために使用するREFERENCE_ARRAYのIDを指定します。このIDを持つARRAY()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの入力値にアクセスすることもできます。
- ic_array_id
- このControl_StateEqnの状態xの初期値を格納するために使用するReference_ArrayのIDを指定します。このIDを持つARYVAL()関数を使用することで、MotionSolveの式のこの状態にアクセスすることができます。また、SYSFNCおよびSYSARYでこのIDを使用することで、ユーザーサブルーチンの初期状態値にアクセスすることもできます。
- type
- モデル化する動的システムのタイプを指定します。"LINEAR"と"USERSUB"のいずれかを選択します。"LINEAR"は、モデル化される動的システムが線形であることを指定します。このシステム定義を行うには、A、B、C、DのマトリクスのIDを指定します。"USERSUB"は、モデル化される動的システムがユーザー定義のサブルーチンで定義されることを指定します。この動的システムは線形でも非線形でもかまいません。 2 3
- a_matrix_id
- 線形のControl_StateEqnの状態マトリクスを含むReference_MatrixオブジェクトのIDを指定します。Aマトリクスは、動的システムの固有のプロパティをカプセル化します。例えば、Aの固有値は、システムの固有値を表します。同様に、Aの固有ベクトルは、動的システムのモード形状を表します。Aは定数値のマトリックスです。これは正則である必要があります。n個の状態がある場合、Aマトリクスの次元はn x nです。type = "LINEAR"の場合にのみ使用します。
- b_matrix_id
- 線形のControl_StateEqnの入力マトリクスを含むReference_MatrixオブジェクトのIDを指定します。Bマトリクスは、入力uの状態方程式への寄与を決定します。
Bは定数値マトリクスです。m個の入力とn個の状態がある場合、Bマトリクスの次元はn x mとなります。
type = "LINEAR"の場合にのみ使用します。
- c_matrix_id
- 線形のControl_StateEqnの出力マトリクスを含むReference_MatrixオブジェクトのIDを指定します。Cマトリクスは、状態xの出力yへの寄与を決定します。Cは定数値マトリクスです。p個の出力とn個の状態がある場合、Cマトリクスの次元はとなります。 n x p
type = "LINEAR"の場合にのみ使用します。
- d_matrix_id
-
線形のControl_StateEqnのフィードスルーマトリクスを含むReference_MatrixオブジェクトのIDを指定します。Dマトリクスは、入力uの出力yへの寄与を決定します。 Dは定数値マトリクスです。p個の出力とm個の入力がある場合、Dマトリクスの次元はp x mとなります。
type = "LINEAR"の場合にのみ使用します。
- num_state
- Control_StateEqnの状態の数を指定する整数。num_state > 0。
type = "USERSUB"の場合にのみ使用します。
- num_output
- Control_StateEqnの出力の数を指定する整数。num_output > 0。
type = "USERSUB"の場合にのみ使用します。
- usrsub_param_string
- データファイルからユーザー定義のサブルーチンGSESUB、GSEXX、GSEXU、GSEYX、GSEYUに渡されるパラメータのリスト。type = "USERSUB"の場合にのみ使用します。この属性は、すべてのタイプのユーザーサブルーチンおよびスクリプトに共通です。 4
- usrsub_dll_name
- ユーザーサブルーチンを含むDLLまたは共有ライブラリのパスと名前を指定します。MotionSolveはこの情報を使用して、実行時にDLL内のユーザーサブルーチンGSESUB、GSEXX、GSEXU、GSEYX、GSEYUを読み込みます。type = "USERSUB"の場合にのみ使用します。
- usrsub_fnc_name
- ユーザーサブルーチンGSESUBの代替名を指定します。
- usrsub_der1_name
- ユーザーサブルーチンGSEXXの代替名を指定します。
- usrsub_der2_name
- ユーザーサブルーチンGSEXUの代替名を指定します。
- usrsub_der3_name
- ユーザーサブルーチンGSEYXの代替名を指定します。
- usrsub_der4_name
- ユーザーサブルーチンGSEYUの代替名を指定します。
- script_name
- usrsub_fnc_nameで指定されたルーチンを含むユーザー作成スクリプトのパスと名前を指定します。
- interpreter
- Specifies the interpreted language that the user script is written in. Valid choices are MATLAB or PYTHON.
例
摩擦は多くの場合、動的システムとしてモデル化されます。この例では、静摩擦と動摩擦の両方が組み込まれたLuGre(Lundt-Grenoble)摩擦モデルの実装を示しています。このモデルには入力、出力、状態があるため、これをControl_StateEqnとして実装することができます。
- σ0
- 摩擦スプリング剛性
- σ1
- 摩擦減衰係数
- σ2
- 粘性減衰係数
- Vs
- 静摩擦遷移速度
- Vd
- 動摩擦遷移速度
- Fc
- 最大クーロン摩擦力 = μd*N
- Fs
- 最大静摩擦力 =μs*N
z は、ブリッスルのたわみを示します。
μs とμdは、静摩擦係数と動摩擦係数です。 N は、垂直抗力の瞬間値です。
- 1入力(m=1):現在の滑り速度v。
- 1状態(n=1):“ブリッスル”のたわみz。
- 1出力(p=1):摩擦力F。
- 7つの設計パラメータ:σ0, σ1, σ2, vs, vd, Fc, Fs。
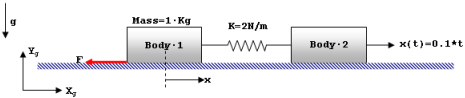
図 2. LuGre摩擦モデルのテスト装置
このモデルは1次元の問題を示しています。運動は全体座標系のX軸方向のみとなります。このシステムは、ボディ1とボディ2の2つの質点からなり、これらは剛性K = 2 N/m。のスプリングによって結合されています。各ボディの質量は1Kgです。これらのボディは全体座標系XY平面に配置されています。ボディ2の質量中心において、全体座標系のx軸方向に、0.1*timeというモーションが適用されます。ボディ1の質量中心はマーカー666で示されています。座標xによって、ボディ1のx方向の変位が定義されます。これは、MotionSolveの式DX(666)によって測定されます。ボディ1の滑り速度は、式VX(666)によって測定されます。
- ボディ1は最初は静止しています。
- ボディ2でのモーション入力を受けて、スプリングが伸びます。スプリング力が増大します。
- 摩擦力Fがスプリング力の反対に作用して、ブリッスルがわずかにたわみます。
- スプリング力が最大静摩擦力に達すると、ボディ1はスライドし始めます。
- ストライベック効果のために、摩擦力が急速に減少します。スプリングが縮んで、スプリング力が減少します。
- 質点が減速して、ストライベック効果のために摩擦力が増大し、モーションが停止します。
- この現象が繰り返されます。
- σ0
- 105N/m
- σ1
- 316.23Ns/m
- σ2
- 0.4Ns/m
- Vs
- 2*10-3m
- Vd
- 2*10-3m
- Fc
- μd*N = 1 N
- Fs
- μs*N = 1.5 N
この例で、Control_StateEqn要素は以下のようになります:
<Control_StateEqn
id = "1"
is_static_hold = "FALSE"
x_solver_array_id = "101"
y_solver_array_id = "102"
u_solver_array_id = "103"
ic_solver_array_id = "104"
type = "USERSUB"
num_state = "1"
num_output = "1"
usrsub_param_string = "USER(666, 1E5, 316.23, 0.4, 1E-3, 2E-3, 1, 1.5)"
usrsub_dll_name = "/staff/olaf/work/Lugre/Lugre.so">
</Control_StateEqn>XとYの配列は次のように定義されます:

UとICの配列は次のように定義されます:

この摩擦モデルに入力を提供するReference_Variableは次のように定義されます:
<Reference_Variable
Id = "1"
Type = "Expression"
Expr = "Vx(666)">
</Reference_Variable> 図 3. LuGreモデルの応答
図 3. LuGreモデルの応答コメント
- Control_StateEqn要素は非常に用途が広いため、多くの分野にわたるシステムのモデル化において、さまざまな用途に適用できます。この要素を使用して、外部定義された複雑なサブシステムをMotionSolveのシステムモデルに埋め込むことができます。外部サブルーチンは、手書きのものであっても、サードパーティアプリケーション全体に対する単なるインターフェースであってもかまいません。MotionSolve内のシステムモデルに“統合”できるサードパーティアプリケーションの例としては、以下が挙げられます:
- MathWorks社の製品であるReal Time Workshopによって生成された、制御システムや油圧システムなどの汎用システム表現。Real Time Workshopは、Simulinkブロック図に対応するCコードを生成できます。
- 独自の内部状態を含む高度なタイヤモデル。
- MotionSolveモデル内の中小サイズの非線形有限要素コンポーネントを定義する非線形有限要素パッケージ。
- 自動車モデル内の人間の運転動作を再現する自動車ドライバモデル。
- 独自の内部状態を含む周波数と振幅に依存するブッシュ。
- "LINEAR"バージョンのControl_StateEqnは、次の図のようにブロック図で表現できます。
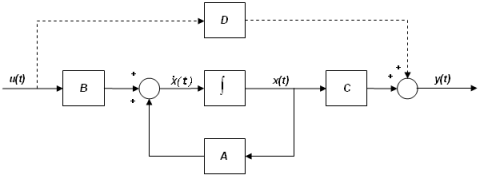
図 4. 線形Control_StateEqnのブロック図表現 - "USERSUB"バージョンのControl_StateEqnもブロック図で表現できます。.
- "USERSUB"バージョンのControl_StateEqnは、ユーザー定義サブルーチンで定義されるほとんどのモデリング要素より複雑です。5つのユーザーサブルーチンが必要となることがあります。まず、GSESUBが必要です。残りの4つ、GSEXX、GSEXU、GSEYX、GSEYUは、stiff積分器(VSTIFFまたはMSTIFF)が使用される場合にのみ必要となります。

図 5.
図 6.
図 7. - 静解析時および擬似静解析時のControl_StateEqn要素に関連する動的状態の挙動は、属性is_static_holdによって制御されます。
is_static_hold = "TRUE"
時間T=0で解析が行われる場合、状態は、IC配列によって指定された値で固定されたままです。動的シミュレーションに続いて解析が行われる場合、値は動的シミュレーションから取得された最後の値で固定されたままです。Control_StateEqnの状態を定義する方程式は、以下に置き換えられます:
x(t*) = x*、ここでx*は定数です。
動的状態が固定されたままの場合、その時間導関数は、入力u(一般的に時間に依存する)が変化しているため、静的平衡または擬似静的ステップの最後でゼロにはならなくなります。これにより、その後動的解析が実行される場合、過渡応答が生じる可能性があります。
is_static_hold = "FALSE"
解析プロセスの間、状態は一定に保たれず、システム全体のコンフィギュレーションの変化に従って変えることができます。これがどのように実現されるかを以下に示します。
静解析および擬似静解析では、動的状態の導関数はゼロに設定されます。これにより、Control_StateEqnが一連の代数方程式に変換されます。
微分方程式は次のようになります:
f(x,u)=0
平衡解析では、システムのコンフィギュレーションが変化すると、平衡条件を満たすように入力uが変化します。上記の式が解かれ、現在のuの値に対するxが計算されます。
この方法により、動的状態の時間導関数が、静解析または擬似静解析の最後でゼロになり、その後の動的シミュレーションで過渡応答が生じるのを回避できます。