/MAT/LAW110 (VEGTER)

ブロックフォーマットのキーワードひずみ速度依存性と熱効果を考慮し、Corus-Vegterの補間された降伏基準とVegterの硬化則を使用した弾塑性構成則。

フォーマット

(1)	(2)	(3)	(5)	(7)	(8)	(9)
/MAT/LAW110/`mat_ID`/`unit_ID`または/MAT/VEGTER/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`		`v`	`Ires`
$I_{c r i t}$	`TAB_YLD`	`MAT_Xscale`	`MAT_Yscale`	$ƒ_{b i}$		$ρ_{b i}^{0}$
$σ_{y l d}^{0}$		$Δ σ_{m}$	$β$	$Ω$		$η$
$ε_{0}$		$σ_{0}^{⋆}$	$Δ G_{0}$	${\dot{ε}}_{0}$		$m$
`T`_ini		`C`_hard	`F`_cut	`VP`	`I`_smooth	`TAB_TEMP`

I_{c r i t}

= 1：

N_{a n g l e}

（試験角度の数、1以上）カードの読み取り

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$f_{u n}$		`R`		$f_{p s}^{1}$		$f_{p s}^{2}$		$f_{s h}$

I_{c r i t}

= 2：

N_{a n g l e}

（試験角度の数、1以上）カードの読み取り

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$f_{u n}$		`R`		$f_{p s}^{1}$		$α_{p s}$		$f_{s h}$

I_{c r i t}

= 3：パラメータ（

N_{a n g l e}

はこのケースでは3に固定されており、0、45、90）の読み取り

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$R_{m}^{0}$		$R_{m}^{45}$		$R_{m}^{90}$		$A_{g}^{0}$		$A_{g}^{45}$
$A_{g}^{90}$		$R^{0}$		$R^{45}$		$R^{90}$

I_{c r i t}

= 4：

N_{a n g l e}

カードの読み取り

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
$f_{u n}$		`R`		$w_{p s}$		$w_{s h}$

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位の識別子（オプション）（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度。（実数）	$[\frac{kg}{m^{3}}]$
`E`	ヤング率。（実数）	$[Pa]$
`v`	ポアソン比。（実数）
`Ires`	マッピングアルゴリズムフラグを返します。 = 1 Nice陽解法。 = 2（デフォルト） Newton反復半陰解法 - 切断面。（整数）
$I_{c r i t}$	Vegter定式化の選択： = 1 従来のVegter定式化。 = 2 標準のVegter定式化。 = 3 Vegter 2017定式化。 = 4 簡易化されたVegter-Lite定式化。（整数）
`TAB_YLD`	表形式の降伏応力 – 塑性ひずみ - ひずみ速度関数の識別子。（整数）
`MAT_Xscale`	表形式の降伏 – 塑性ひずみ - ひずみ速度関数のXスケールファクター。デフォルト = 10（実数）
`MAT_Yscale`	表形式の降伏 – 塑性ひずみ - ひずみ速度関数のYスケールファクター。デフォルト = 1.0（実数）
$ƒ_{b i}$	2軸スケールファクター。（実数 > 0.0）
$ρ_{b i}^{0}$	RDに対して0度の方向の2軸ひずみ速度比率。（実数 > 0.0）
$σ_{y l d}^{0}$	初期降伏応力（実数）	$[Pa]$
$Δ σ_{m}$	硬化応力増分。（実数）	$[Pa]$
$β$	大ひずみ硬化パラメータ。（実数）
$Ω$	微小ひずみ硬化パラメータ。（実数）
$η$	硬化指数（実数）
$ε_{0}$	初期塑性ひずみ（実数）
$σ_{0}^{⋆}$	限界動的流れ応力。（実数）	$[Pa]$
$Δ G_{0}$	最大活性化エンタルピー。（実数）	$[eV]$
${\dot{ε}}_{0}$	熱活性化運動の限界ひずみ速度。（実数）	$[Hz]$
$m$	ひずみ速度挙動指数。（実数）
`T`_ini	初期温度。（実数）	$[K]$
`C`_hard	硬化係数。 = 0 =硬化は完全等方性モデルです。 = 1 硬化は運動学的Prager-Zieglerモデルです。 = 0～1の値硬化は2つのモデル間で補間されます。（実数）
`F`_cut	ひずみ速度フィルタリングのカットオフ周波数。デフォルト = 1.0 x 10²⁰（実数）	$[Hz]$
`VP`	ひずみ速度選択フラグ = 1 降伏応力に対するひずみ速度効果は塑性ひずみ速度に依存します。 = 2（デフォルト）降伏に対するひずみ速度効果は全ひずみ速度に依存します。 = 3 降伏に対するひずみ速度効果は偏差ひずみ速度に依存します。（整数）
`I`_smooth	補間タイプ（表形式降伏関数の場合）。 = 1 線形補間。 = 2 対数補間（底10）。 = 3 対数補間（底n）。（整数）
`TAB_TEMP`	表形式の降伏応力 – 塑性ひずみ - 温度の識別子。（整数）
$f_{u n}$	単軸スケールファクター。（実数 > 0.0）
`R`	Lankford係数。デフォルト = 1.0（実数 > 0.0）
$f_{p s}^{1}$	平面ひずみスケールファクターの第1成分。（実数 > 0.0）
$f_{p s}^{2}$	平面ひずみスケールファクターの第2成分（ $I_{c r i t}$ = 1）。（実数 > 0.0）
$α_{p s}$	平面ひずみスケールファクターの第2成分を計算するための平均ファクター（ $I_{c r i t}$ = 2）。デフォルト = 0.5（実数 > 0.0）
$f_{s h}$	せん断倍率（実数 > 0.0）
$R_{m}^{i}$	回転方向（RD）を基準にして $i$ 度の方向の最大単軸工学応力（ $I_{c r i t}$ = 3）。（実数 > 0.0）
$A_{g}^{i}$	回転方向（RD）を基準にして $i$ 度の方向の最大単軸均一伸張量（％単位）（ $I_{c r i t}$ = 3）。（実数 > 0.0）
$A_{g}^{i}$	回転方向（RD）を基準にして $i$ 度の方向のLankford係数（ $I_{c r i t}$ = 3）。デフォルト = 1.0（実数 > 0.0）
$w_{p s}$	平面ひずみ重み係数（ $I_{c r i t}$ = 4）。（実数 > 0.0）
$w_{s h}$	せん断重み係数（ $I_{c r i t}$ = 4）。（実数 > 0.0）

例

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/25
Local unit system
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW110/1/25
Steel: Icrit = 1, example with 3 angles (0Â°, 45Â° and 90Â° to the RD)
#        Init. dens.
             7.85E-9
#                  E                  nu
            194200.0                 0.3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#    Icrit   TAB_YLD          MAT_Xscale          MAT_Yscale                 fBI               rhoBI            
         1         0                 0.0                 0.0               1.004               0.889                         
#               YLD0               DSIGM                BETA               OMEGA                   n
               107.1               179.6                0.25                8.07                 1.0
#               EPS0                SIGS                 DG0               Deps0                   m
                 0.0                20.0                 800             3.61e-3                 1.0
#               TINI              C_HARD               F_CUT        VP   Ismooth  TAB_TEMP
               293.0                 0.0             10000.0         1         1         0
#          fUN_THETA             R_THETA          fPS1_THETA          fPS2_THETA           fSH_THETA 
               1.021                0.64               1.061              0.5305               0.560
               0.987                0.48               1.037              0.5185               0.640 
               1.009                0.76               1.048              0.5240               0.560 
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW110/2/25
Steel :Icrit = 2, example with 3 angles (0Â°, 45Â° and 90Â° to the RD)
#        Init. dens.
             7.85E-9
#                  E                  nu
            194200.0                 0.3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#    Icrit   TAB_YLD          MAT_Xscale          MAT_Yscale                 fBI               rhoBI            
         2         0                 0.0                 0.0               1.004               0.889                         
#               YLD0               DSIGM                BETA               OMEGA                   n
               107.1               179.6                0.25                8.07                 1.0
#               EPS0                SIGS                 DG0               Deps0                   m
                 0.0                20.0                 800             3.61e-3                 1.0
#               TINI              C_HARD               F_CUT        VP   Ismooth  TAB_TEMP
               293.0                 0.0             10000.0         1         1         0
#          fUN_THETA             R_THETA          fPS1_THETA          ALPS_THETA           fSH_THETA 
               1.021                0.64               1.061                 0.5               0.560
               0.987                0.48               1.037                 0.5               0.640 
               1.009                0.76               1.048                 0.5               0.560 
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW110/3/25
Steel
#        Init. dens.
             7.85E-9
#                  E                  nu
            194200.0                 0.3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#    Icrit   TAB_YLD          MAT_Xscale          MAT_Yscale                 fBI               rhoBI            
         3         0                 0.0                 0.0               1.004               0.889                         
#               YLD0               DSIGM                BETA               OMEGA                   n
               107.1               179.6                0.25                8.07                 1.0
#               EPS0                SIGS                 DG0               Deps0                   m
                 0.0                20.0                 800             3.61e-3                 1.0
#               TINI              C_HARD               F_CUT        VP   Ismooth  TAB_TEMP
               293.0                 0.0             10000.0         1         1         0
#               RM_0               RM_45               RM_90                AG_0               AG_45
               408.4               408.4               408.4                20.0                20.0
#              AG_90                 R_0                R_45                R_90
                20.0                0.64                0.48                0.76    
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW110/4/25
Steel :example with 3 angles (0Â°, 45Â° and 90Â° to the RD)
#        Init. dens.
             7.85E-9
#                  E                  nu
            194200.0                 0.3
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#    Icrit   TAB_YLD          MAT_Xscale          MAT_Yscale                 fBI               rhoBI            
         4         0                 0.0                 0.0               1.004               0.889                         
#               YLD0               DSIGM                BETA               OMEGA                   n
               107.1               179.6                0.25                8.07                 1.0
#               EPS0                SIGS                 DG0               Deps0                   m
                 0.0                20.0                 800             3.61e-3                 1.0
#               TINI              C_HARD               F_CUT        VP   Ismooth  TAB_TEMP
               293.0                 0.0             10000.0         1         1         0
#          fUN_THETA             R_THETA                W_PS                W_SH
               1.021                0.64              0.4125                0.75
               0.987                0.48              0.4125                0.75
               1.009                0.76              0.4125                0.75 
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#enddata

$I_{c r i t}$ = 1の場合、この材料則では、次のように定義される従来のVegter降伏基準が使用されます：
(1)
$ϕ = \bar{σ} - σ_{Y}$

ここで、

$ϕ$

降伏関数。

$σ_{Y}$

降伏応力。

$\bar{σ}$

補間されたVegter相当応力。

平面応力条件下のVegter 降伏局面は、主応力空間で3つの2次ベジェ補間曲線を定義することで得られます。（図 1）。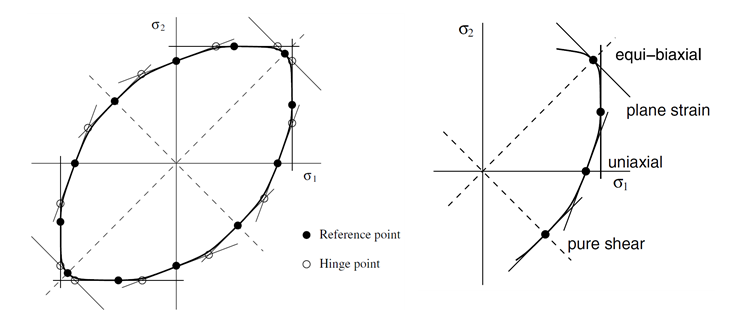

図 1. 平面応力における従来のVegter定式化によって定義された降伏基準（I_crit=1）

これらの曲線を使用して、異なる荷重条件（せん断、単軸引張、平面ひずみ、等2軸引張）で実験的に測定された4つの参照ポイントがリンクされます。2つの参照ポイント間で、降伏局面が次のように定義されます：(2)
$σ = (\begin{matrix} σ_{1} \\ σ_{2} \end{matrix}) = \bar{σ} (\begin{matrix} f_{1} \\ f_{2} \end{matrix}) = (\begin{matrix} σ_{1}^{r 1} \\ σ_{2}^{r 1} \end{matrix}) + 2 μ (\begin{matrix} σ_{1}^{r 1} - σ_{1}^{h} \\ σ_{2}^{r 1} - σ_{2}^{h} \end{matrix}) + μ^{2} (\begin{matrix} σ_{1}^{r 2} + σ_{1}^{r 1} - 2 σ_{1}^{h} \\ σ_{2}^{r 2} + σ_{2}^{r 1} - 2 σ_{2}^{h} \end{matrix})$

ここで、

$σ^{r 1}$ 、 $σ^{r 2}$

2つの参照ポイント。

$σ^{h}$

ヒンジポイント（自動的に計算されます）。

$μ$

各時間ステップで計算される、降伏局面上の位置を特定するパラメータ。

測定された4つの参照ポイントは次のように表されます： $f_{s h}$ 、 $f_{u n}$ 、 $f_{p s}$ 、 $ƒ_{b i}$ 。これらの参照ポイントの座標はユーザーが指定します。

ここで、 $f_{s h}^{2}$ = $- f_{s h}^{1} = - f_{s h}$ 、 $f_{u n}^{2} = 0$ 、 $f_{b i}^{2} = f_{b i}^{1} = f_{b i}$ です。回転方向を基準にして指定された方向について、せん断 $f_{s h}$ 、単軸引張 $f_{u n}$ 、等2軸引張の参照ポイント $ƒ_{b i}$ には、1つの成分のみを設定する必要があります。平面ひずみ参照ポイントについては、2つの成分 $f_{p s}^{1}$ と $f_{p s}^{2}$ をユーザーが指定する必要があります。

2つ目の座標 $f_{p s}^{2}$ は自由に選択できます。この座標が設定されていない場合は、2つの隣接するヒンジポイントの2つ目の座標の平均が、この座標の値として使用されます。

2つの参照ポイントの間に配置されるヒンジポイントは、それらの参照ポイントの座標に加え、各参照ポイントの降伏曲面の法線も使用して計算されます。降伏曲面の法線は、法線則により、ひずみ速度テンソル成分を使用して次のように表すことができます：(3)
$n = (\begin{matrix} n_{1} \\ n_{2} \end{matrix}) = (\begin{matrix} {\dot{ε}}_{1} \\ {\dot{ε}}_{2} \end{matrix}) = (\begin{matrix} 1 \\ \frac{{\dot{ε}}_{2}}{{\dot{ε}}_{1}} \end{matrix}) = (\begin{matrix} 1 \\ ρ_{r} \end{matrix})$

ここで、 $ρ^{r}$ は指定された参照ポイントのひずみ速度比率です。せん断の参照ポイントについては、 $ρ_{s h} = - 1$ です。平面ひずみの参照ポイントについては、 $ρ_{p s} = 0$ です。単軸引張の参照ポイントについては、この比率は、Lankford係数（ $R$ ）を使用して次のように計算できます：(4)
$ρ_{u n} = \frac{- R}{R + 1}$

Lankford係数はユーザーが指定する必要があります。最後に、等2軸引張 $ƒ_{b i}$ のひずみ速度比率も設定する必要があります。
$I_{c r i t}$ = 2の場合は、標準のVegter基準が使用されます。これは従来のVegterと同じ基準ですが、入力カードが異なります。このカードで、平面ひずみポイントの2つ目の座標は、2つの隣接するヒンジポイントの2つ目の座標 $σ_{h 1}$ および $σ_{h 2}$ の加重平均として次のように計算されます：
(5)
$f_{p s}^{2} = σ_{h 1}^{2} + α_{p s} (σ_{h 2}^{2} - σ_{h 1}^{2})$
$I_{c r i t}$ = 3の場合は、Vegter 2017降伏基準が使用されます。これは従来のVegterと同じ基準ですが、入力カードが異なります。このカード内のすべてのパラメータは、最大単軸工学応力 $R_{m}^{i}$ 、最大均一伸張量 $A_{g}^{i}$ 、およびLankford係数 $R^{i}$ によって決定されます。これら3つのパラメータは、回転方向（RD）を基準にして角度 $i$ 度の3つの方向（0度、45度、90度）について指定する必要があります。この基準では、角度の数は3に固定されています。
$I_{c r i t}$ = 4の場合、この材料則では、次のように定義される簡易化されたVegter Lite降伏基準が使用されます：
(6)
$ϕ = \bar{σ} - σ_{Y}$

ここで、

$ϕ$

降伏関数。

$σ_{Y}$

降伏応力。

$\bar{σ}$

補間されたVegter相当応力。

平面応力条件下のVegter 降伏局面は、主応力空間内で2つの2次Nurbs補間曲線を定義することで得られます。これらの曲線を使用して、異なる荷重条件（単軸圧縮、単軸引張、等2軸引張）で実験的に測定された3つの参照ポイントがリンクされます。2つの参照ポイント間で、降伏局面が次のように定義されます：(7)
$σ = (\begin{matrix} σ_{1} \\ σ_{2} \end{matrix}) = \bar{σ} (\begin{matrix} f_{1} \\ f_{2} \end{matrix}) = \frac{{(1 - μ)}^{2} (\begin{matrix} σ_{1}^{r 1} \\ σ_{2}^{r 1} \end{matrix}) + 2 μ (1 - μ) w_{h} (\begin{matrix} σ_{1}^{h} \\ σ_{2}^{h} \end{matrix}) + μ^{2} (\begin{matrix} σ_{1}^{r 2} \\ σ_{2}^{r 2} \end{matrix})}{{(1 - μ)}^{2} + 2 μ (1 - μ) w_{h} + μ^{2}}$
(8)
$0 \leq μ \leq 1, w_{h} \geq 0$

ここで、

$σ^{r 1}$ 、 $σ^{r 2}$

2つの参照ポイント。

$σ^{h}$

ヒンジポイント（自動的に計算されます）。

$μ$

各時間ステップで計算される、降伏局面上の位置を特定するパラメータ。

$w_{h}$

ヒンジポイントに関連付けられた重み係数。

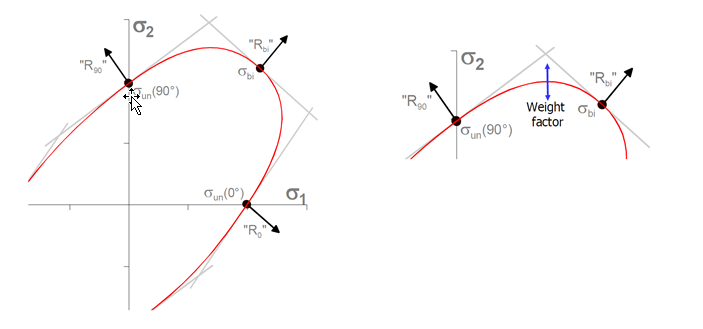
図 2. 平面応力における従来のVegter定式化によって定義された降伏基準（I_crit=2）

図 2では、降伏基準は、平面応力における従来のVegter定式化によって定義されています（ $I_{c r i t}$ = 2）。

従来のVegter定式化の場合、パラメータ $f_{u n}$ 、 $ƒ_{b i}$ 、 $R$ 、 $ρ_{b i}$ を設定する必要があります。この簡易化された定式化では、2つのヒンジポイントは純せん断状態と平面ひずみ状態にあります。2つの関連付けられた重み係数 $w_{s h}$ と $w_{p s}$ も定義する必要があります。
異方性を考慮するには、回転方向RDを基準にして異なる角度 $ϕ$ のいくつかの $N_{a n g l e}$ 方向について一連のパラメータを定義します。これらの方向は、0と $\frac{π}{2}$ の間に均等に分散されている必要があります。指定された複数の方向の間に配置されたすべての荷重方向について、Vegterモデルではフーリエ級数補間の使用が提示されています。
各方向に対してすべてのパラメータを定義する必要はありません。パラメータ $ƒ_{b i}$ は、すべての方向について同じです。方向0（回転方向）のひずみ速度比率 $ρ_{b i}$ だけで、他のすべての方向のこの比率を特定できます。(9)
$ρ_{b i} (θ) = \frac{(ρ_{b i} + 1) + (ρ_{b i} - 1) \cos 2 θ}{(ρ_{b i} + 1) - (ρ_{b i} - 1) \cos 2 θ}$

他のすべてのパラメータでは、次のフーリエ補間が使用されます：(10)
$f_{u n} (θ) = \sum_{m = 0}^{N_{a n g l e} - 1} ψ_{un}^{m} cos (2 m θ)$

従来、標準、および2017のVegter定式化（ $I_{c r i t}$ = 1、2、3）では、同様の処理が行われます。 (11)
$f_{s h}^{2} (θ) = - f_{s h}^{1} (\frac{π}{2} - θ)$

簡易化されたVegter Lite定式化（ $I_{c r i t}$ = 4）では、同様の補間が $R$ 、 $w_{s h}$ 、 $w_{p s}$ に対して行われます。この場合、次のようになります：(12)
$w_{s h} (θ) = w_{s h} (\frac{π}{2} - θ)$
パラメータによって凸状の降伏局面が定義される必要があります。定義されない場合は、シミュレーションが不安定になる可能性があります。このため、Radioss Starterには降伏基準の凸性を確認するためのデータチェックが用意されています。
1つの方向のみが定義されている場合（ $N_{a n g l e}$ = 1）、この材料則は等方性であるため、/PROP/TYPE1（等方性シェル）と組み合わせて使用される必要があります。複数の方向が定義されている場合（ $N_{a n g l e}$ > 1または $I_{c r i t}$ = 3）、この材料則は異方性になるため、/PROP/TYPE9（直交異方性シェル）と組み合わせて使用される必要があります。
降伏応力 $σ_{Y}$ は次の式によって定義されます：
(13)
$σ_{Y} = σ_{0} + Δ σ_{m} [β (ε_{p} + ε_{0}) + {(1 - e^{- Ω (ε_{p} + ε_{0})})}^{n}] + σ_{0}^{⋆} {[1 + \frac{k T}{Δ G_{0}} \ln (\frac{\dot{ε}}{\dot{ε_{0}}})]}^{m}$

ここで、

$σ_{0}$

初期降伏応力

$Δ σ_{m}$

硬化応力増分。

$β$

大ひずみ硬化パラメータ。

$ε_{0}$

初期塑性ひずみ

$Ω$

微小ひずみ硬化パラメータ。

$η$

硬化指数

$σ_{0}^{⋆}$

限界動的流れ応力。

$k$

ボルツマン定数

$T$

温度

$Δ G_{0}$

最大活性化エンタルピー。

${\dot{ε}}_{0}$

非粘性極限ひずみ速度。

$m$

ひずみ速度依存性指数。

パラメータ $Ω$ は、微小ひずみ時の硬化曲線に強い影響を与える効果があるため、微小ひずみ硬化パラメータと呼ばれます（図 3a）。同様に、大ひずみ硬化パラメータは大ひずみ時に大きな影響を与えます（図 3b）。

図 3. 硬化パラメータが降伏応力の評価に及ぼす影響
T_iniが定義されている場合、シミュレーション全体にわたって、温度はT_iniの値で一定です。これにより、ひずみ速度依存性が一定になります（図 4a）。
熱活性化効果（温度上昇後のひずみ速度依存性の微増）を考慮するために温度変化を計算する場合は、/HEAT/MATオプションを定義する必要があります（図 4a）。

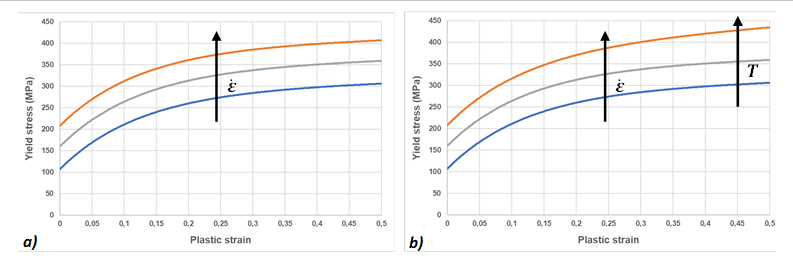
図 4. 温度設定がひずみ速度依存性に及ぼす影響
ひずみ速度 $\dot{ε}$ の計算は、次のようにフラグ $V P$ の値に依存します：
- $V P$ = 1の場合：塑性ひずみ速度が使用されます。
- $V P$ = 2の場合：全ひずみ速度が使用されます。
- $V P$ = 3の場合：偏差ひずみ速度が使用されます。
どの場合でも、ひずみ速度の計算には、カットオフ周波数 $F_{c u t}$ を使用したフィルタリングが含まれます。このカットオフ周波数は、次の関係を満たすようにユーザーによって定義されます：(14)
${\dot{ε}}_{f} = α {\dot{ε}}^{n} + (1 - α) {\dot{ε}}^{n - 1}$

ここで、 $α = 2 π F_{c u t} Δ t$ 。
表形式の硬化降伏応力を使用する場合は、表形式関数TAB_YLDのIDを定義する必要があります。このテーブルを使用して、複数のひずみ速度で、塑性ひずみに応じたいくつかの降伏応力変化を定義できます。X方向とY方向に2つのスケールファクターを定義することもできます。この場合は、硬化パラメータ $σ_{0}$ 、 $Δ σ_{m}$ 、 $β$ 、 $Ω$ 、 $η$ は無視され、降伏応力は次のようになります：(15)
$σ_{Y} = f_{Y} (ε_{p}, \dot{ε})$

さらに、断熱条件での熱軟化を考慮するために、塑性ひずみと温度TAB_TEMPを使用して表形式の降伏応力を定義することもできます。この場合、降伏応力は次のようになります：(16)
$σ_{Y} = f_{Y} (ε_{p}, \dot{ε}) \frac{f_{temp} (ε_{p}, T)}{f_{temp} (ε_{p}, T_{ini})}$

ここで、

T_ini

参照温度。

$T$

/HEAT/MATオプションを使用して計算される実際の温度。
係数C_hardを設定することで、移動硬化を使用することもできます：
- C_hard = 0の場合：等方性硬化が使用されます。
- C_hard = 1の場合： Prager-Ziegler移動硬化が使用されます。
- 0 ≤ C_hard ≤ 1の場合：等方性硬化と移動硬化の間でモデルが補間されます。
  
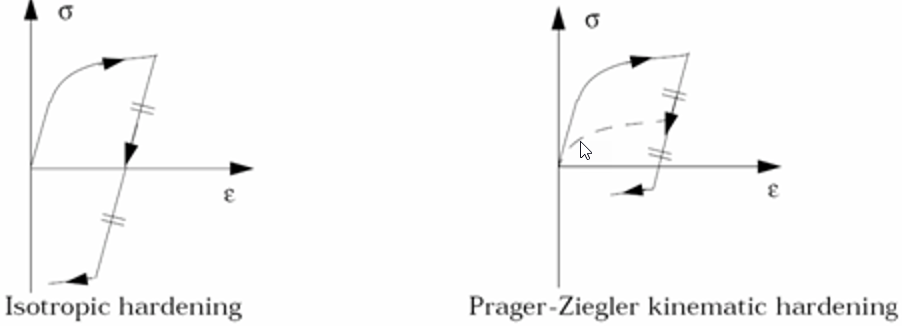
  図 5.

/MAT/LAW110 (VEGTER)

フォーマット

定義

例

コメント