ブロックフォーマットのキーワード 修正Mohr破壊基準を使用して異方性Hill材料を記述します。この材料則は、シェルおよびソリッドに対して使用可能です。
フォーマット
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
/MAT/LAW72 /mat_ID unit_ID /MAT/HILL_MMC /mat_ID unit_ID
mat_title
ρ
i
E v
σ y 0
ε p 0 n F G
H N L M
C 1 C 2 C 3 m D c
定義
フィールド
内容
SI単位の例
mat_ID 材料識別子(整数、最大10桁)
unit_ID 単位識別子 (整数、最大10桁)
mat_title 材料のタイトル(文字、最大100文字)
ρ
i
初期密度(実数)
[
kg
m
3
]
E 初期ヤング率(実数)
[
Pa ]
v ポアソン比(実数)
σ
y
0
初期降伏応力デフォルト = 1020 (実数)
[
Pa ]
ε
p
0
初期塑性ひずみ(実数)
n Swift硬化の等方性関数の指数部:
σ
y
=
σ
y
0
(
ε
p
+
ε
p
0
)
n
MMC破壊方程式の指数部としても使用します。 2
デフォルト = 1.0(実数)
F , G , H , L , M , N 6つのHILL材料 異方性パラメータ(> 0)(実数)
C 1 MMC破壊モデルの第1パラメータ(実数)
C 2 MMC破壊モデルの第2パラメータデフォルト =
σ
y
0
(実数)
[
Pa ]
C 3 MMC破壊モデルの第3パラメータ(実数)
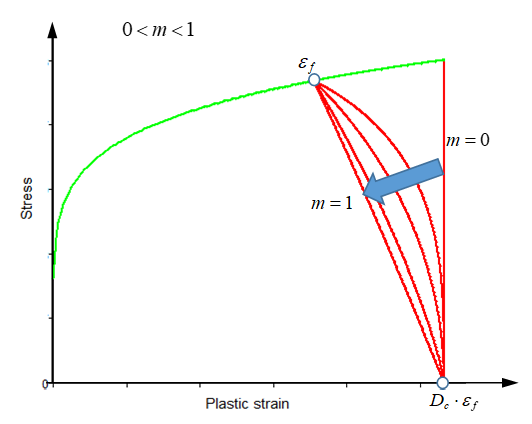
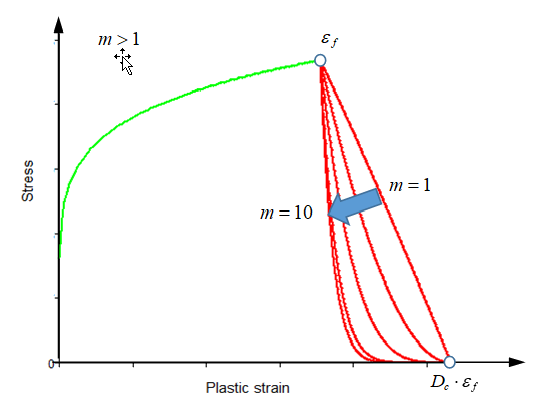
m 軟化関数の指数部 3 デフォルト = 1.0(実数)
D c 臨界損傷
= 1 (デフォルト)
損傷が1に達すると要素は削除されます。
> 1
降伏応力は軟化関数によって修正されます 3
損傷が臨界損傷値に達すると、要素は削除されます。
(実数)
例(金属)
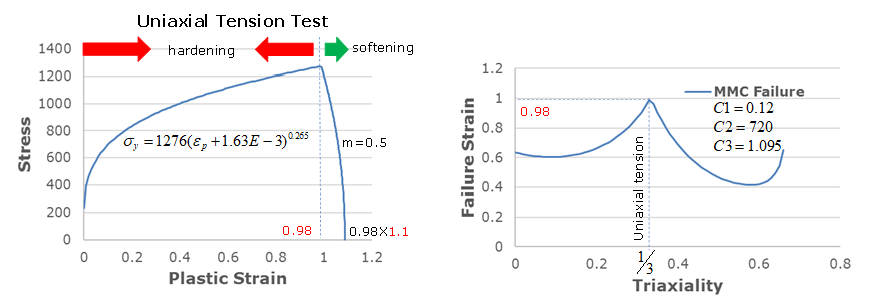
この材料の例では、材料の軟化と破断を検討します。MMCパラメータ
C 1 、
C 2 、および
C 2 を使用して、単軸引張試験における破断ひずみが0.98と計算されます。
m =0.5とした単軸引張試験では0.98で材料の軟化が始まり、
0.98
×
D
c
MathType@MTEF@5@5@+=
feaagKart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaaIWaGaai
OlaiaaiMdacaaI4aGaey41aqRaamiramaaBaaaleaacaWGJbaabeaa aaa@3E4D@
に達するまで継続します。
図 1.
#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
g mm ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#- 2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW72/1/1
Metal
# RHO_I
0.0028
# E nu
200E+3 0.3
# Sig0 Eps0 n F G
1276 1.63E-3 0.265 0.5 0.5
# H N L M
0.5 1.5 0 0
# C1 C2 C3 m Dc
0.12 720 1.095 0.5 1.1
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
コメント
3D等価Hill応力は:(1)
f
=
F
(
σ
yy
−
σ
zz
)
2
+
G
(
σ
zz
−
σ
xx
)
2
+
H
(
σ
xx
−
σ
yy
)
2
+
2
L
σ
yz
2
+
2
M
σ
zx
2
+
2
N
σ
xy
2
シェル要素の場合:
(2)
f
=
F
σ
yy
2
+
G
σ
xx
2
+
H
(
σ
xx
−
σ
yy
)
2
+
2
N
σ
xy
2
MMC破壊基準は:(3)
D
=
∫
0
ε
p
d
ε
p
ε
f
(
θ
,
η
)
ここで、
(4)
ε
f
(
θ
¯
,
η
)
=
{
σ
y
0
C
2
[
C
3
+
3
2
−
3
(
1
−
C
3
)
(
sec
(
θ
¯
π
6
)
−
1
)
]
[
1
+
C
1
2
3
cos
(
θ
¯
π
6
)
+
C
1
(
η
+
1
3
sin
(
θ
¯
π
6
)
)
]
}
−
1
n
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH1oqzda
WgaaWcbaGaamOzaaqabaGcdaqadaqaaiqbeI7aXzaaraGaaiilaiab
eE7aObGaayjkaiaawMcaaiabg2da9maacmGabaWaaSaaaeaacqaHdp
WCdaqhaaWcbaGaamyEaaqaaiaaicdaaaaakeaacaWGdbWaaSbaaSqa
aiaaikdaaeqaaaaakmaadmGabaGaam4qamaaBaaaleaacaaIZaaabe
aakiabgUcaRmaalaaabaWaaOaaaeaacaaIZaaaleqaaaGcbaGaaGOm
aiabgkHiTmaakaaabaGaaG4maaWcbeaaaaGcdaqadiqaaiaaigdacq
GHsislcaWGdbWaaSbaaSqaaiaaiodaaeqaaaGccaGLOaGaayzkaaWa
aeWaceaaciGGZbGaaiyzaiaacogadaqadiqaamaalaaabaGafqiUde
NbaebacqaHapaCaeaacaaI2aaaaaGaayjkaiaawMcaaiabgkHiTiaa
igdaaiaawIcacaGLPaaaaiaawUfacaGLDbaadaWadiqaamaakaaaba
WaaSaaaeaacaaIXaGaey4kaSIaam4qamaaDaaaleaacaaIXaaabaGa
aGOmaaaaaOqaaiaaiodaaaaaleqaaOGaci4yaiaac+gacaGGZbWaae
WaceaadaWcaaqaaiqbeI7aXzaaraGaeqiWdahabaGaaGOnaaaaaiaa
wIcacaGLPaaacqGHRaWkcaWGdbWaaSbaaSqaaiaaigdaaeqaaOWaae
WaceaacqaH3oaAcqGHRaWkdaWcaaqaaiaaigdaaeaacaaIZaaaaiGa
cohacaGGPbGaaiOBamaabmGabaWaaSaaaeaacuaH4oqCgaqeaiabec
8aWbqaaiaaiAdaaaaacaGLOaGaayzkaaaacaGLOaGaayzkaaaacaGL
BbGaayzxaaaacaGL7bGaayzFaaWaaWbaaSqabeaacqGHsisldaWcaa
qaaiaaigdaaeaacaWGUbaaaaaaaaa@84F9@
3次元ソリッド要素の場合
η
は応力の3軸性で、
η
=
1
3
(
σ
x
x
+
σ
y
y
+
σ
z
z
)
σ
V
M
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH3oaAcq
GH9aqpdaWcaaqaamaalaaabaGaaGymaaqaaiaaiodaaaWaaeWaceaa
cqaHdpWCdaWgaaWcbaGaamiEaiaadIhaaeqaaOGaey4kaSIaeq4Wdm
3aaSbaaSqaaiaadMhacaWG5baabeaakiabgUcaRiabeo8aZnaaBaaa
leaacaWG6bGaamOEaaqabaaakiaawIcacaGLPaaaaeaacqaHdpWCda
WgaaWcbaGaamOvaiaad2eaaeqaaaaaaaa@4E7B@
θ
¯
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacuaH4oqCga qeaaaa@3935@
はシフトLode角
θ
¯
=
1
−
2
π
a
r
cos
ζ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacuaH4oqCga
qeaiabg2da9iaaigdacqGHsisldaWcaaqaaiaaikdaaeaacqaHapaC
aaGaamyyaiaadkhaciGGJbGaai4BaiaacohacqaH2oGEaaa@44D9@
で、Lode角(
θ
)パラメータ
ζ
=
cos
(
3
θ
)
=
27
2
J
3
σ
V
M
3
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH2oGEcq
GH9aqpciGGJbGaai4BaiaacohadaqadaqaaiaaiodacqaH4oqCaiaa
wIcacaGLPaaacqGH9aqpdaWcaaqaaiaaikdacaaI3aaabaGaaGOmaa
aadaWcaaqaaiaadQeadaWgaaWcbaGaaG4maaqabaaakeaacqaHdpWC
daqhaaWcbaGaamOvaiaad2eaaeaacaaIZaaaaaaaaaa@4A74@
J
3
は偏差応力の第3不変量
シェル要素に対して
η
は応力の3軸性で、
η
=
1
3
(
σ
x
x
+
σ
y
y
+
σ
z
z
)
σ
V
M
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH3oaAcq
GH9aqpdaWcaaqaamaalaaabaGaaGymaaqaaiaaiodaaaWaaeWaceaa
cqaHdpWCdaWgaaWcbaGaamiEaiaadIhaaeqaaOGaey4kaSIaeq4Wdm
3aaSbaaSqaaiaadMhacaWG5baabeaakiabgUcaRiabeo8aZnaaBaaa
leaacaWG6bGaamOEaaqabaaakiaawIcacaGLPaaaaeaacqaHdpWCda
WgaaWcbaGaamOvaiaad2eaaeqaaaaaaaa@4E7B@
θ
¯
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacuaH4oqCga qeaaaa@3935@
はShift Lode角
θ
¯
=
1
−
2
π
a
r
cos
ζ
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacuaH4oqCga
qeaiabg2da9iaaigdacqGHsisldaWcaaqaaiaaikdaaeaacqaHapaC
aaGaamyyaiaadkhaciGGJbGaai4BaiaacohacqaH2oGEaaa@44D9@
で、Lode角(
θ
)パラメータ
ζ
=
cos
(
3
θ
)
=
−
27
2
η
(
η
2
−
1
3
)
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacqaH2oGEcq
GH9aqpciGGJbGaai4BaiaacohadaqadaqaaiaaiodacqaH4oqCaiaa
wIcacaGLPaaacqGH9aqpcqGHsisldaWcaaqaaiaaikdacaaI3aaaba
GaaGOmaaaacqaH3oaAdaqadaqaaiabeE7aOnaaCaaaleqabaGaaGOm
aaaakiabgkHiTmaalaaabaGaaGymaaqaaiaaiodaaaaacaGLOaGaay zkaaaaaa@4D7E@
MMC破壊基準による破壊と損傷:
アニメーションファイルにユーザー変数を(Engineの/ANIM/Eltyp/Restype で)表示可能で、時刻歴ファイルに(Starterの/TH/SHEL と/TH/BRIC )で表示可能です:
/ANIM/BRICK/DAMG 、/ANIM/SHELL/DAMG 、/H3D/SHELL/DAMG および/H3D/SOLID/DAMG を使用して、正規化された損傷変数
D
n
=
D
D
c
MathType@MTEF@5@5@+=
feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqGqFfpeea0xe9vq=Jb9
vqpeea0xd9q8qiYRWxGi6xij=hbba9q8aq0=yq=He9q8qiLsFr0=vr
0=vr0db8meaabaqaciGacaGaaeqabaWaaeaaeaaakeaacaWGebWaaS
baaSqaaiaad6gaaeqaaOGaeyypa0ZaaSaaaeaacaWGebaabaGaamir
amaaBaaaleaacaWGJbaabeaaaaaaaa@3D15@
をアニメーションファイルに表示することもできます。