/MAT/LAW57 (BARLAT3)

ブロックフォーマットのキーワードこの材料則は、ユーザー定義関数で塑性硬化を記述します。これはシェル要素のみで使用できます。

これは、アルミニウム合金等の異方性材料の成形加工のモデル化に使用される弾塑性直交異方性材料則です。この材料則は、プロパティセットタイプ/PROP/TYPE9（SH_ORTH）または/PROP/TYPE10（SH_COMP）と共に使用する必要があります。

フォーマット

(1)	(3)	(5)	(7)	(9)
/MAT/LAW57/`mat_ID`/`unit_ID`または/MAT/BARLAT3/`mat_ID`/`unit_ID`
`mat_title`
$ρ_{i}$
`E`	$ν$
`fct_ID`_E	`E`_inf	`C`_E
`r`₀₀	`r`₄₅	`r`₉₀	`C`_hard	`m`
$ε_{p}^{m a x}$	$ε_{t}$	$ε_{m}$	`F`_cut	`F`_smooth

各塑性関数毎に次の行を繰り返します

(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)
`fct_ID`_i		`Fscale`_i		${\dot{ε}}_{i}$

定義

フィールド	内容	SI単位の例
`mat_ID`	材料識別子（整数、最大10桁）
`unit_ID`	単位識別子。（整数、最大10桁）
`mat_title`	材料のタイトル（文字、最大100文字）
$ρ_{i}$	初期密度（実数）	$[\frac{kg}{m^{3}}]$
`E`	ヤング率（実数）	$[Pa]$
$ν$	ポアソン比（実数）
`fct_ID`_E	ヤング率のスケールファクターの関数ID（ヤング率が塑性ひずみの関数である場合） 11 デフォルト = 0：この場合はヤング率の進展は`E`_infおよび`C`_Eに応じて決まります。（整数）
`E`_inf	無限の塑性ひずみに対する飽和ヤング率（実数）
`C`_E	ヤング率進展のパラメータ（実数）
`r`₀₀	0°のランクフォードパラメータデフォルト = 1.0（実数）
`r`₄₅	45°のランクフォードパラメータデフォルト = 1.0（実数）
`r`₉₀	90°のランクフォードパラメータデフォルト = 1.0（実数）
`C`_hard	硬化係数。 = 0 硬化は完全等方性モデルです。 = 1 硬化は運動学的Prager-Zieglerモデルです。 = 0～1の値硬化は2つのモデル間で補間されます。（実数）
`m`	Barlatパラメータ = 6.0（デフォルト）体心立法（BCC）材料用 = 8.0 面心立法（FCC）材料用（実数）
$ε_{p}^{m a x}$	破壊塑性ひずみ。デフォルト = 1.0 x 10³⁰（実数）
$ε_{t}$	応力が減少し始める引張破壊ひずみ。デフォルト = 1.0 x 10³⁰（実数）
$ε_{m}$	要素内の応力が0に設定される最大引張破壊ひずみ。デフォルト = 2.0 x 10³⁰（実数）
`F`_cut	ひずみ速度フィルタリングのカットオフ周波数。デフォルト = 10000 Hz （実数）	$[Hz]$
`F`_smooth	ひずみ速度スムージングオプションフラグ。 = 0（デフォルト）ひずみ速度を平滑化しません。 = 1 ひずみ速度スムージングはアクティブ。（整数）
`fct_ID`_i	塑性曲線の`i`番目の関数の識別子（整数）
`Fscale`_i	`i`番目の関数のスケールファクターデフォルトは1.0に設定されます（実数）
${\dot{ε}}_{i}$	`i`番目の関数のひずみ速度（実数）	$[\frac{1}{s}]$

例（鋼材）

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                   g                  mm                  ms
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW57/1/1
Steel
#              RHO_I
                .008                   
#                  E                  NU
              206000                  .3
#FUNCT_IDE                          EINF                  CE
         0                             0                   0
#                r00                 r45                 r90              C_hard                   m
                1.79                1.51                2.27                   0                   0
#           EPSP_max               EPS_T               EPS_M                Fcut  Fsmooth
                   0                   0                   0                  10        1
# funct_ID                      Fscale_i               EPS_i
         5                             0                   0                                        
         5                             0                   1                                        
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  3. FUNCTIONS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/FUNCT/5
function_5
#                  X                   Y
                   0                 157                                                            
                  .1                 320                                                            
                  .5                 480                                                            
                 1.2                 600                                                            
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

平面応力の異方性降伏基準Fは、下記によって定義されます：(1)
$F = a {| K_{1} + K_{2} |}^{m} + a {| K_{1} - K_{2} |}^{m} + c {| 2 K_{2} |}^{m} - 2 {σ_{y}}^{m} = 0$

ここで、

$σ_{y}$ は降伏応力

$K_{1} = \frac{σ_{x x} + h σ_{y y}}{2}$ および $K_{2} = \sqrt{{(\frac{σ_{x x} - h σ_{y y}}{2})}^{2} + p^{2} σ_{x y}^{2}}$
ランクフォードパラメータの角度は、直交異方性方向1に対して定義されます。材料定数a、c、h、pは、次の3つのLankfordパラメータから取得されます：(2)
$\begin{array}{l} a = 2 - 2 \sqrt{\frac{r_{00}}{1 + r_{00}}} \sqrt{\frac{r_{90}}{1 + r_{90}}} \\ c = 2 - a \\ h = \sqrt{\frac{r_{00}}{1 + r_{00}}} \sqrt{\frac{1 + r_{90}}{r_{90}}} \end{array}$

材料定数pは次の式から算出できます：(3)
$\frac{2 m \cdot σ_{y}^{m}}{(\frac{\partial F}{\partial σ_{x x}} + \frac{\partial F}{\partial σ_{y y}}) σ_{45}} - 1 - r_{45} = 0$
最初の（静的）関数の最後のポイントの応力が0に等しい場合、 $ε_{p}^{m a x}$ のデフォルト値は $ε_{p}$ の対応値に設定されます。
$ε_{p}$ （塑性ひずみ）が1つの積分点で $ε_{p}^{\max}$ に到達すると、対応するシェル要素が削除されます。
最大主ひずみが $ε_{1} > ε_{t}$ の場合、応力は次の関係式に従って減少します：(4)
$σ = σ (\frac{ε_{m} - ε_{1}}{ε_{m} - ε_{t}})$
$ε_{1} > ε_{m}$ の場合、応力は0に減少します（ただし、要素は削除されません）。
曲線の最大数は10です。
$\dot{ε} \leq {\dot{ε}}_{n}$ の場合、降伏はf_nとf_n-1の間で補間されます。
$\dot{ε} \leq {\dot{ε}}_{1}$ の場合、関数f₁が使用されます。
${\dot{ε}}_{\max}$ を超えた場合、降伏は外挿されます。

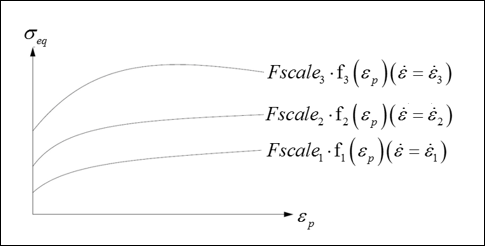
図 1.
ヤング率の進展：
- fct_ID_E > 0であれば、この曲線は等価な塑性ひずみによるヤング率の進展に対するスケールファクターを定義します。これは、関数 $f ({\bar{ε}}_{p})$ によって以下のようにヤング率がスケーリングされることを意味します：(5)
  $E (t) = E \cdot f ({\bar{ε}}_{p})$
  
  このスケールファクターの初期値は1で、この値から減少していきます。
- fct_ID_E = 0の場合、ヤング率は次のように計算されます：(6)
  $E (t) = E - (E - E_{i n f}) [1 - \exp (- C_{E} {\bar{ε}}_{p})]$
  
  ここで、EとE_infはそれぞれ初期と漸近するヤング率の値で、 ${\bar{ε}}_{p}$ は累積の相当塑性ひずみです。
  
  注: fct_ID_E = 0でC_E = 0の場合、ヤング率Eが一定になります。
パラメータF_smoothとF_cutは、ひずみ速度のフィルタリングを可能にします。3つのケースが設定できます：
- F_smooth = 0 および F_cut = 0.0の場合、ひずみ速度フィルタリングはオフ。
- F_smooth = 1 および F_cut = 0.0の場合、ひずみ速度フィルタリングは、デフォルトのカットオフ周波数10 kHzを使用。
- F_cut ≠ 0, F_smoothの場合、自動的に1に設定され、ひずみ速度フィルタリングは、指定されたカットオフ周波数を使用。

/MAT/LAW57 (BARLAT3)

フォーマット

定義

例（鋼材）

コメント