/MAT/LAW78

塑性変形では、降伏曲面が境界曲面内部を移動するだけでそのサイズは変化しません。境界曲面はサイズと位置の両方が変化します。この法則では、ヤング率の塑性ひずみ依存性と加工硬化停滞の影響も考慮されます。SPHに関してはソリッドにのみ適合し、/SPH/WavesCompressionテストで検証できます。ソリッドのバージョンは等方性のみです。シェルのバージョンはHill規準に基づいた異方性です。

フォーマット

定義

例

#RADIOSS STARTER
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/UNIT/1
unit for mat
                  Mg                  mm                   s
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#-  2. MATERIALS:
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
/MAT/LAW78/1/1
DP600-HDG
#              RHO_I
              7.8E-9
#                  E                  NU
              206000                  .3
#                  Y                   B                C2KH                   H                  B0
                 420                 112                 200                   0                 555
#                  m                RSAT      OPTR                  C1                  C2
                  12                 190         0                   1                   1
#                 R0                 R45                 R90                Mexp     Icrit
                   1                   1                   1
#  Fct_IDE                          EINF                  CE                C1KH
         0                        163000                  50                   0
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|
#ENDDATA
/END
#---1----|----2----|----3----|----4----|----5----|----6----|----7----|----8----|----9----|---10----|

コメント

1. ソリッド要素ではvon Mises降伏基準が用いられ、その降伏関数は次のように表されます：(1)
   $$f=\frac{3}{2}\left(\mathbf{s}-\mathbf{\alpha }\right):\left(\mathbf{s}-\mathbf{\alpha }\right)-Y^2$$
   シェル要素ではHill（1948）またはBarlat（1989）の降伏基準を使用します。これによって、異方性材料をモデル化できます。

   • Hillの基準は次の式で表すことができます。(2)
     $$f=\phi (\mathbf{\sigma }-\mathbf{\alpha })-Y^2$$
     ここで、

     $Y$

     降伏応力。

     $\alpha$

     全逆応力。

     $A=\sigma -\alpha$ ,であれば、 $\phi$ は次のようになります。(3)

     $$\phi (A)=A_{xx}^2-\frac{2r_0}{1+r_0}{A}_{xx}{A}_{yy}+\frac{r_0\left(1+r_{90}\right)}{r_{90}\left(1+r_0\right)}{A}_{yy}^2+\frac{r_0+r_{90}}{r_{90}\left(1+r_0\right)}\left(2r_{45}+1\right)A_{xy}^2$$
   • Barlatの基準は次の式で表すことができます。(4)
     $$f=\varphi \left(\sigma -\alpha \right)-2Y^M$$

     $M$ はBarlatの降伏基準の指数部です。

     $\varphi$ は次のように記述できます。(5)

     $$\varphi \left(A\right)=a{\left|K_1+K_2\right|}^M+ a{\left|K_1-K_2\right|}^M+c{\left|2K_2\right|}^M$$

     ここで、

     $K_1= \frac{A_{xx}+h{A}_{yy}}{2}$ および $K_2=\sqrt{{\left(\frac{A_{xx}-h{A}_{yy}}{2}\right)}^2+p^2{A}_{xy}^2}$ となります。

     $a$ 、 $c$ 、および $h$ の各パラメータはランクフォード係数から算出されます。

     $a=2-2\sqrt{\frac{r_{00}}{1+r_{00}} \frac{r_{90}}{1+r_{90}}}$ 、 $c=2-a$ 、 $h= \sqrt{\frac{r_{00}}{1+r_{00}} \frac{1+r_{90}}{r_{90}}}$

     パラメータ $p$ は次の式を解くことで求めることができます。(6)

     $$\frac{2M{Y}^M}{\left(\frac{\partial f}{\partial A_{xx}}+ \frac{\partial f}{\partial A_{yy}}\right){\sigma }_{45}}-1-r_{45}=0$$
2. 降伏応力、ポアソン比、およびヤング率は真に正にする必要があります。その他のパラメータは非負値にする必要があります。
3. 2曲面モデルの慨略図を図 1に示します。
   ここで、0は降伏曲面の元の中心であり、中心 $\alpha$ と半径Yを持つ降伏曲面がB+Rによって指定されたサイズと中心の位置を示すテンソル $\mathbf{\beta }$ を持つ境界曲面内部を運動学的に移動しています。

   
   
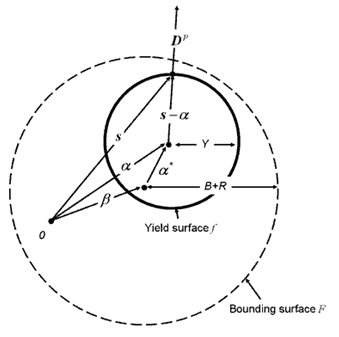
   図 1. 2曲面モデルの概略図

4. 降伏曲面は移動硬化を受けます。その移動は以下の式の ${\mathbf{\alpha }}^{*}$ により記述されます：
   • シェル要素に対して(7)
     $${\dot{\alpha }}^{*}=C\left[\left(\frac{a}{Y}\right)\left(\mathbf{\sigma }-\mathbf{\alpha }\right)-\sqrt{\frac{a}{\Vert {\mathbf{\alpha }}^{\text{*}}\Vert }}{\mathbf{\alpha }}^{*}\right]{\dot{\overline{\epsilon }}}_p$$
   • ソリッド要素に対して(8)
     $${\dot{\alpha }}^{*}=C\left[\left(\frac{2}{3}\right)a{\dot{\epsilon }}_{{}^{\mathbf{p}}}-\sqrt{\frac{a}{\Vert {\mathbf{\alpha }}^{*}\Vert }}{\mathbf{\alpha }}^{*}{\dot{\overline{\epsilon }}}_{{}^P}\right]$$
   ここで、

   ${\dot{\overline{\epsilon }}}_p$

   相当塑性ひずみ速度

   Cおよびa

   材料パラメータおよび $a=B+R-Y$

   $\mathbf{\alpha }={\mathbf{\alpha }}^{*}+\mathbf{\beta }$

   全逆応力

   注: 2次（HillまたはBarlatで $M$ = 2.0を使用）および等方性基準（ $r_{00}= r_{45}=r_{90}=1$ ）の場合、シェルの運動方程式はソリッドの運動方程式に等しくなります。
5. 移動硬化則に関するパラメータ $C$ は、順方向および逆方向の変形の加工硬化速度の変化を記述するために2つの異なる値を取ることができます。
   • $C_1^{KH}>C_2^{KH}$ の場合、 $\{\begin{array}{c}\begin{array}{ccc}C=C_1^{KH}& \text{if}& Max\left(\Vert {\alpha }^{*}\Vert \right)<B-Y\end{array}\\ \begin{array}{ccc}C=C_2^{KH}& \text{otherwise}& \begin{array}{cc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& \end{array}\end{array}\end{array}$
   • $C_1^{KH}\le C_2^{KH}$ の場合、加工硬化速度の変化は無効になり、 $C=C_2^{KH}$ になります。
6. 境界曲面は等方-移動硬化を受けます。等方硬化の進展の式は:

   $\dot{R}=m\left(R_{\mathit{sat}}-R\right){\dot{\overline{\epsilon }}}_{{}^p}$

   デフォルト（OptR = 0の場合）のYoshidaの表現

   $R=R_{\mathit{sat}}\left[{\left(C_1+{\overline{\epsilon }}_{{}^p}\right)}^{C_2}-C_1^{C_2}\right]$

   OptR = 1の場合、シェル要素でのみ使用可能

   境界曲面の移動硬化の進展の式は：

   • シェル要素に対して：(9)
     $$\dot{\beta }=m\left[\left(\frac{b}{Y}\right)\left(\sigma -\alpha \right)-\beta \right]{\dot{\overline{\epsilon }}}_{{}^p}$$
   • ソリッド要素に対して：(10)
     $$\dot{\beta }=m\left(\frac{2}{3}b{\dot{\epsilon }}_{{}^p}-\beta {\dot{\overline{\epsilon }}}_{{}^p}\right)$$
   注: 2次（HillまたはBarlatでMexp = 2を使用）および等方性基準（ $r_{00}= r_{45}=r_{90}=1$ ）の場合、シェルの移動硬化方程式はソリッドの移動硬化方程式に等しくなります。
7. 除荷の間の加工硬化の停滞はJ₂-タイプの曲面 $g_{\sigma }$ を半径rと中心qを用いて表現されます：(11)
   $$\begin{array}{l}{g}_{\sigma }(\mathbf{\beta },{\mathbf{q}}^{\prime },r)=\frac{3}{2}(\mathbf{\beta }-{\mathbf{q}}^{\prime }):(\mathbf{\beta }-{\mathbf{q}}^{\prime })-r^2\\ {\dot{\mathbf{q}}}^{\prime }=\text{μ}\left(\mathbf{\beta }-{\mathbf{q}}^{\prime }\right)\\ r=h\dot{\Gamma }\hspace{0.17em},\dot{\Gamma }\frac{3\left(\mathbf{\beta }-{\mathbf{q}}^{\prime }\right):\dot{\beta }}{2r}\end{array}$$
   ここで、

   $h\left(0<h\le 1\right)$

   曲面 $g_{\sigma }$ の膨張速度を決定する材料パラメータを示します。

   $\mathbf{\beta }$

   曲面 $g_{\sigma }$ の内側か曲面上です。

8. Barlatの降伏基準（1989）の指数部は、材料の微細構造を考慮することによって設定できます。2.0を上回る値であれば有効ですが、一般的には次のように設定します。
   • Mexp = 6.0（デフォルト）： 体心立法（BCC）材料の場合
   • Mexp = 8.0： 面心立法（FCC）材料の場合
9. ヤング率の進展：
   • fct_ID_E > 0であれば、この曲線は等価な塑性ひずみによるヤング率の進展に対するスケールファクターを定義します。これは、関数 $\mathrm{f}\left({\overline{\epsilon }}_p\right)$ によって以下のようにヤング率がスケーリングされることを意味します：
     • $E\left(t\right)=E\cdot \mathrm{f}\left({\overline{\epsilon }}_p\right)$

     このスケールファクターの初期値は1で、この値から減少していきます。

   • fct_ID_E = 0の場合、ヤング率は次のように計算されます：(12)

     $$E\left(t\right)=E-\left(E-E_{\mathit{inf}}\right)\left[1-\exp \left(-C_E{\overline{\epsilon }}_p\right)\right]$$
     ここで、

     E および E_inf

     それぞれ初期と漸近するヤング率の値。

     ${\overline{\epsilon }}_p$

     累積の相当塑性ひずみ。

     注: fct_ID_E = 0でC_E = 0の場合、ヤング率Eが一定になります。
10. この材料則は陰解法解析では利用できません。